大阪大学 理系数学 2020年 第1問 解説

今回は、大阪大学理系数学（2020年 第1問）の解説をしたいと思います。

問題

　関数
$$f(x)=(x+1)^{\frac{1}{x+1}}\quad(x\geqq0)$$について，以下の問いに答えよ．

⑴　$f(x)$ の最大値を求めよ．

⑵　$f(x)$ とその導関数の極限
$$\displaystyle\lim_{x\to\infty}f(x),\quad\displaystyle\lim_{x\to\infty}f'(x)$$をそれぞれ求めよ．ただし，
$$\displaystyle\lim_{x\to\infty}\dfrac{\log x}{x}=0$$であることを用いてもよい．

⑶　$y=f(x)$ のグラフの概形をかけ．ただし，グラフの凹凸を調べる必要はない．

（大阪大学）

解答

⑴

$f(x)=(x+1)^{\frac{1}{x+1}}$ より
$$\log f(x)=\dfrac{\log(x+1)}{x+1}$$

両辺を微分すると
$$\begin{align}
\dfrac{f'(x)}{f(x)} &= \dfrac{1-\log(x+1)}{(x+1)^2} \\[0.3em]
\therefore \ f'(x) &= \dfrac{1-\log(x+1)}{(x+1)^2}\cdot f(x)
\end{align}$$

$x\gt0$ において $f(x)\gt0$ であるから、$f(x)$ の増減表は次のようになる。

$$\begin{array}{c||c|c|c|c}\hline
x & 0 & \cdots & e-1 & \cdots \\ \hline
f'(x) & & + & 0 & – \\ \hline
f(x) & 1 & \nearrow & e^{\frac{1}{e}} & \searrow \\ \hline
\end{array}$$

よって、$f(x)$ は $x=e-1$ のとき最大値 $\boldsymbol{e^{\frac{1}{e}}}$ をとる。

⑵

$$\displaystyle\lim_{x\to\infty}\log f(x)=\displaystyle\lim_{x\to\infty}\dfrac{\log(x+1)}{x+1}=0$$であり、対数関数は連続なので
$$\begin{align}
\log\displaystyle\lim_{x\to\infty}f(x) &= 0 \\[0.3em]
\therefore \ \displaystyle\lim_{x\to\infty}f(x) &= e^0=\mathbf{1}
\end{align}$$

また、⑴より
$$f'(x)=\left\{\dfrac{1}{(x+1)^2}-\dfrac{1}{x+1}\cdot\dfrac{\log(x+1)}{x+1}\right\}f(x)$$と表せるので
$$\displaystyle\lim_{x\to\infty}f'(x)=(0-0\cdot0)\cdot1=\mathbf{0}$$

⑶

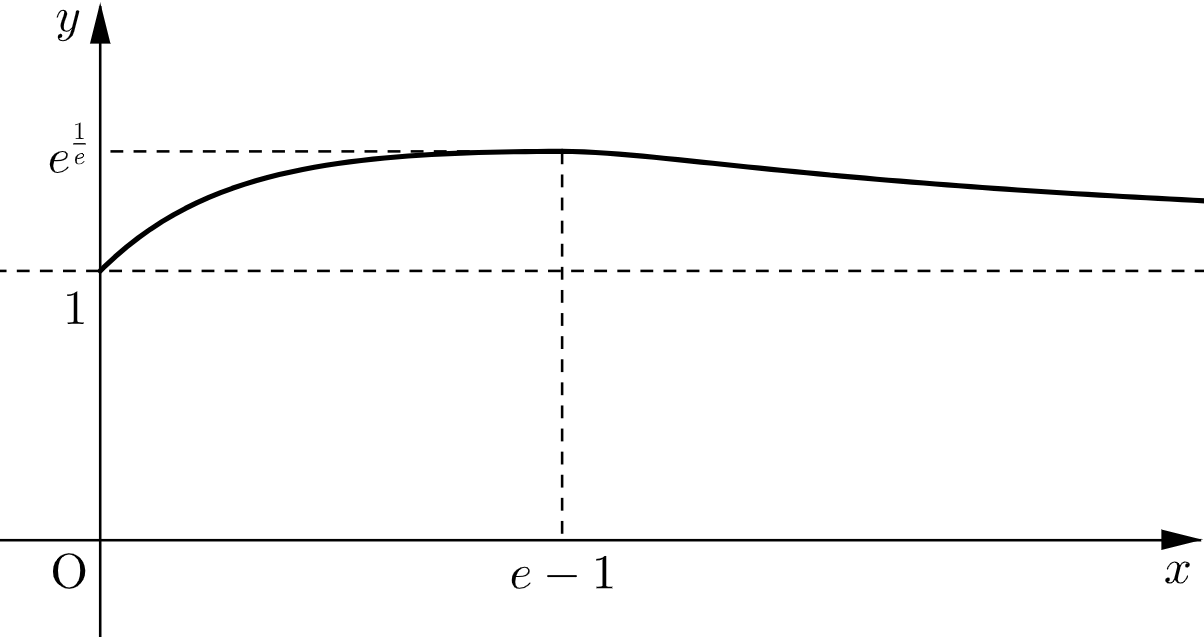
⑴,⑵より、$y=f(x)$ のグラフの概形は下図のようになる。

解説

グラフの概形を問う基本的な問題です。

$(\text{変数})^{(\text{変数})}$ の形をした関数の微分は $\log$ をとった後でないとできないので注意しましょう。

まとめ

今回は、大阪大学理系数学（2020年 第1問）の解説をしました。