神戸大学 理系数学 2022年 第4問 解説

今回は、神戸大学理系数学（2022年 第4問）の解説をしたいと思います。

問題

$a$ を正の実数とし，双曲線 $\dfrac{x^2}{4}-\dfrac{y^2}{4}=1$ と直線 $y=\sqrt{ a }x+\sqrt{ a }$ が異なる $2$ 点 $\mathrm{P},\mathrm{Q}$ で交わっているとする．線分 $\mathrm{PQ}$ の中点を $\mathrm{R}(s,t)$ とする．以下の問に答えよ．

⑴　$a$ のとりうる値の範囲を求めよ．

⑵　$s,t$ の値を $a$ を用いて表せ．

⑶　$a$ が⑴で求めた範囲を動くときに $s$ のとりうる値の範囲を求めよ．

⑷　$t$ の値を $s$ を用いて表せ．

（神戸大学）

解答

⑴

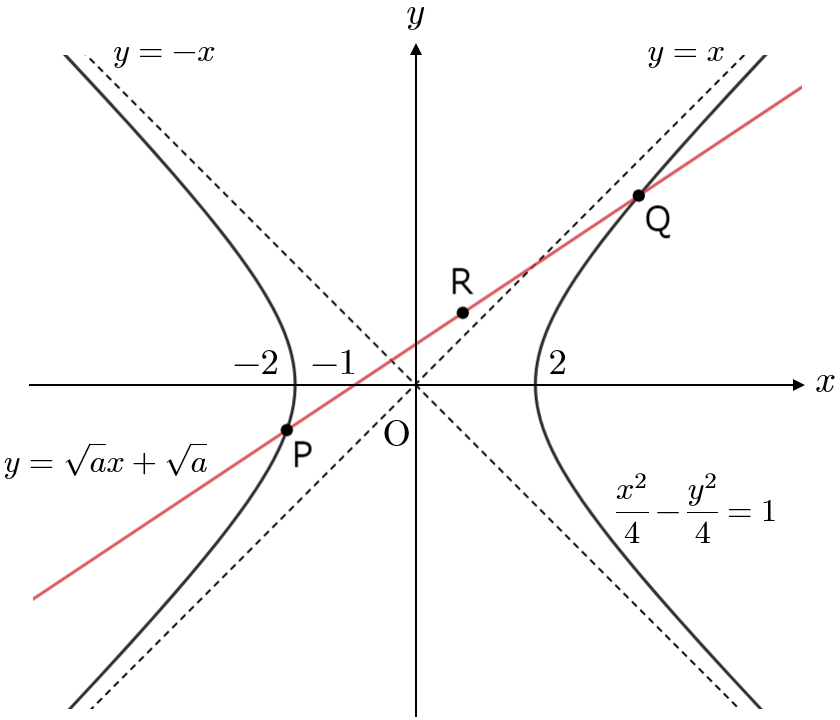
$\dfrac{x^2}{4}-\dfrac{y^2}{4}=1 \quad \cdots \text{①}$、$y=\sqrt{ a }x+\sqrt{ a } \quad \cdots \text{②}$ とする。

①に②を代入すると
$$\begin{eqnarray}
\dfrac{x^2}{4}-\dfrac{1}{4}\left(\sqrt{ a }x+\sqrt{ a }\right)^2&=&1 \\
x^2-a\left(x^2+2x+1\right)&=&4 \\[0.5em]
(a-1)x^2+2ax+a+4&=&0 \quad \cdots \text{③}
\end{eqnarray}$$

①と②が異なる $2$ 点で交わるとき、③は異なる $2$ つの実数解をもつ。

(ⅰ)　$a=1$ のとき
③より
$$2x+5=0 \quad \Longleftrightarrow \quad x=-\dfrac{5}{2}$$となり、実数解は $1$ つなので不適。

(ⅱ)　$0 \lt a \lt 1, \ 1 \lt a$ のとき
③の判別式を $D$ とすると、$D \gt 0$ より
$$\begin{array}{c}
\begin{eqnarray}
\dfrac{D}{4}&=&a^2-(a-1)(a+4) \\
&=&-3a+4 \gt 0
\end{eqnarray} \\[0.5em]
a \lt \dfrac{4}{3}
\end{array}$$$0 \lt a \lt 1, \ 1 \lt a$ より
$$0 \lt a \lt 1, \ 1 \lt a \lt \dfrac{4}{3}$$

(ⅰ),(ⅱ)より、$a$ のとりうる値の範囲は
$$\boldsymbol{0 \lt a \lt 1, \ 1 \lt a \lt \dfrac{4}{3}} \quad \cdots \text{④}$$

⑵

$\mathrm{P},\mathrm{Q}$ の $x$ 座標をそれぞれ $\alpha,\beta$ とすると、これらは③の異なる $2$ つの実数解である。

解と係数の関係より
$$\alpha+\beta = -\dfrac{2a}{a-1}$$であり、$\mathrm{R}$ は線分$\mathrm{PQ}$ の中点であるから、
$$s=\dfrac{\alpha+\beta}{2}=\boldsymbol{-\dfrac{a}{a-1}} \quad \cdots \text{⑤}$$とわかる。また $\mathrm{R}$ は②上の点なので
$$\begin{eqnarray}
t&=&\sqrt{ a }s+\sqrt{ a } = \sqrt{ a }\left(-\dfrac{a}{a-1}+1\right) \\
&=& \boldsymbol{-\dfrac{\sqrt{ a }}{a-1}} \quad \cdots \text{⑥}
\end{eqnarray}$$

⑶

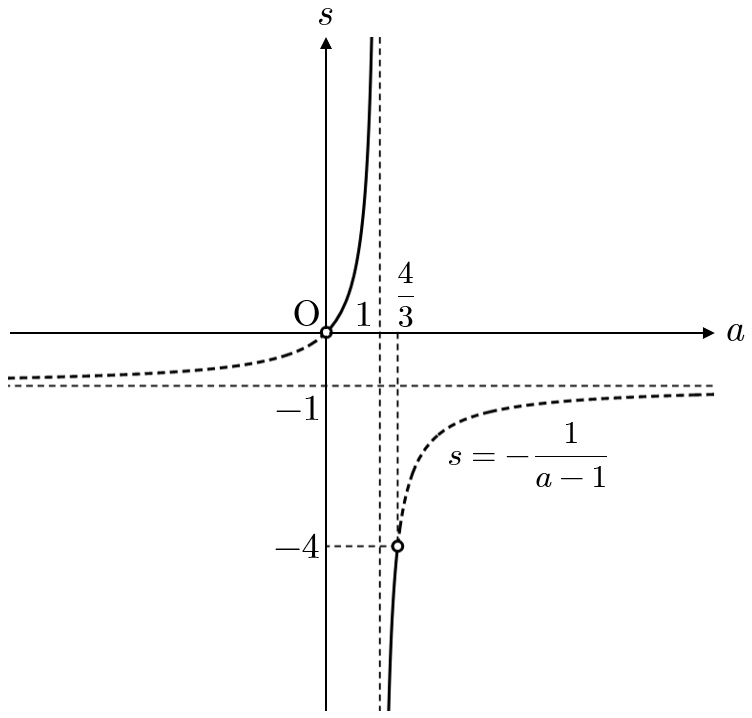
$s=-\dfrac{a}{a-1}=-1-\dfrac{1}{a-1}$ であるから、④と上の図より、$s$ のとりうる値の範囲は
$$\boldsymbol{s \lt -4, \ 0 \lt s}$$

⑷

$a \ne 0$ なので、⑥より $t \ne 0$ とわかる。よって、⑤,⑥より
$$\dfrac{s}{t} = -\dfrac{a}{a-1} \cdot \left( -\dfrac{a-1}{\sqrt{ a }} \right) = \sqrt{ a } \quad \cdots \text{⑦}$$

⑥に⑦を代入すると
$$t=-\dfrac{\dfrac{s}{t}}{\dfrac{s^2}{t^2}-1}=\dfrac{s}{t-\dfrac{s^2}{t}}$$左辺と右辺に $t-\dfrac{s^2}{t}$ をかけると
$$\begin{eqnarray}
t^2-s^2 &=& s \\
t^2 &=& s^2+s \\
\end{eqnarray}$$⑶の結果から $s^2+s=s(s+1) \gt 0$であるから
$$t = \pm \sqrt{ s^2+s }$$

$\sqrt{ a } \gt 0$ と⑦より $\dfrac{s}{t} \gt 0$ であるから、$s$ と $t$ の正負は一致する。

したがって、⑶の結果と合わせて
$$t=
\begin{cases}
\boldsymbol{-\sqrt{ s^2+s }} & \mathbf{\text{（}} \ \boldsymbol{s \lt -4} \ \mathbf{\text{のとき）}} \\[0.3em]
\boldsymbol{\sqrt{ s^2+s }} & \mathbf{\text{（}} \ \boldsymbol{s \gt 0} \ \mathbf{\text{のとき）}}
\end{cases}$$

解説

誘導に乗って計算すれば、そこまで難しいところはありませんが、細かい議論が必要な部分もあるので注意が必要です。

$2$ 次の係数に文字が入っている場合は、$2$ 次の係数が $0$ かそうでないかの場合分けが必要です。

ちなみに、⑴の答えは $0 \lt a \lt 1$ と $1 \lt a \lt \dfrac{4}{3}$ の $2$ つの部分に分かれていますが、$0 \lt a \lt 1$ のときは解答の図のように「 $x \lt 0$ と $x \gt 0$ のそれぞれにおいて $1$ 点ずつ交わる」という状況を、$1 \lt a \lt \dfrac{4}{3}$ のときは「 $x \lt 0$ において異なる $2$ 点で交わる」という状況を表します。
また $a=1$ のときは漸近線 $y=x$ と傾きが一致するため、双曲線 $\text{①}$ と直線 $\text{②}$ は $1$ 点でしか交わりません。

⑷では「 $s$ を用いて」と言われているので、$a$ を消去するのが自然な発想です。その際、$s$ と $t$ の正負が一致するため答えに場合分けが必要になるところがポイントです。

まとめ

今回は、神戸大学理系数学（2022年 第4問）の解説をしました。