神戸大学 理系数学 2022年 第2問 解説

今回は、神戸大学理系数学（2022年 第2問）の解説をしたいと思います。

問題

$m$ を $3$ 以上の自然数，$\theta = \dfrac{2\pi}{m}$，$C_1$ を半径 $1$ の円とする．円 $C_1$ に内接する（すべての頂点が $C_1$ 上にある）正 $m$ 角形を $P_1$ とし，$P_1$ に内接する（ $P_1$ のすべての辺と接する）円を $C_2$ とする．同様に，$n$ を自然数とするとき，円 $C_n$ に内接する正 $m$ 角形を $P_n$ とし，$P_n$ に内接する円を $C_{n+1}$ とする．$C_n$ の半径を $r_n$，$C_n$ の内側で $P_n$ の外側の部分の面積を $s_n$ とし，$f(m)=\displaystyle \sum_{n=1}^{\infty} s_n$ とする．以下の問に答えよ．

⑴　$r_n, \ s_n$ の値を $\theta , \ n$ を用いて表せ．

⑵　$f(m)$ の値を $\theta$ を用いて表せ．

⑶　極限値 $\displaystyle \lim_{ m \to \infty } f(m)$ を求めよ．
ただし，必要があれば $\displaystyle \lim_{ x \to 0 } \dfrac{x-\sin x}{x^3} = \dfrac{1}{6}$ を用いてよい．

（神戸大学）

解答

⑴

対称性からすべての円の中心は $1$ 点で一致し、その点を $\mathrm{O}$ とする。

また、正 $m$ 角形 $P_n$ の隣り合う $2$ つの頂点を $\mathrm{A}_n, \ \mathrm{B}_n$ とし、辺 $\mathrm{A}_n \mathrm{B}_n$ の中点を $\mathrm{M}_n$ とする。

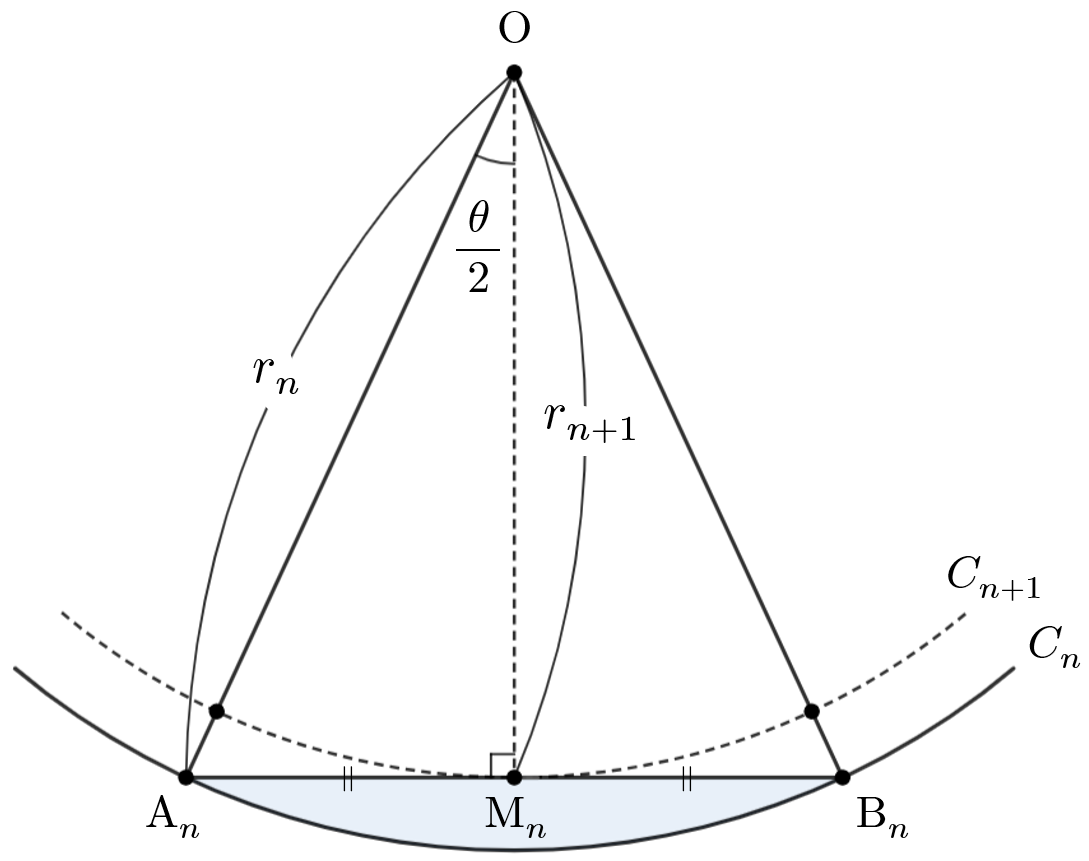
$\mathrm{OA}_n = \mathrm{OB}_n =r_n$ より $\triangle \mathrm{OA}_n\mathrm{B}_n$ は二等辺三角形なので、$\mathrm{OM}_n \perp \mathrm{A}_n \mathrm{B}_n$ であり、円 $C_{n+1}$ は $\mathrm{M}_n$ で辺 $\mathrm{A}_n \mathrm{B}_n$ に接する。よって、$\mathrm{OM}_n = r_{n+1}$ となる。

また、$\angle \mathrm{A}_n\mathrm{OB}_n = \dfrac{2\pi}{m} = \theta$ より
$$\angle \mathrm{A}_n\mathrm{OM}_n = \angle \mathrm{B}_n\mathrm{OM}_n = \dfrac{1}{2} \angle \mathrm{A}_n\mathrm{OB}_n = \dfrac{\theta}{2}$$であるから、
$$r_{n+1} = r_n \cos \dfrac{\theta}{2}$$となる。

したがって、数列 $\{r_n\}$ は初項 $r_1=1$、公比 $\cos \dfrac{\theta}{2}$ の等比数列となり、
$$r_n = 1 \cdot \cos^{n-1} \dfrac{\theta}{2} = \boldsymbol{\cos^{n-1} \dfrac{\theta}{2}}$$

また、$s_n$ は円 $C_n$ から正 $m$ 角形 $P_n$ を引いた部分の面積であり、$P_n$ の面積は $\triangle \mathrm{OA}_n\mathrm{B}_n$ の面積 $m\left( = \dfrac{2\pi}{\theta} \right)$ 個分なので、
$$\begin{eqnarray}
s_n &=& \pi r_n^{\,2} \ – \ \dfrac{2\pi}{\theta} \cdot \dfrac{1}{2}r_n^{\,2} \sin \theta \\
&=& \pi r_n^{\,2} \left( 1-\dfrac{\sin \theta}{\theta} \right) \\
&=& \pi \cos^{2n-2} \dfrac{\theta}{2} \cdot \dfrac{\theta \ – \ \sin \theta}{\theta}\\
&=& \boldsymbol{\dfrac{\pi(\theta \ – \ \sin \theta)}{\theta} \cos^{2n-2} \dfrac{\theta}{2}}
\end{eqnarray}$$

⑵

⑴より、$f(m)$ は初項 $\dfrac{\pi(\theta \ – \ \sin \theta)}{\theta}$、公比 $\cos^2 \dfrac{\theta}{2}$ の無限等比級数である。

また $m \geqq 3$ より $0 \lt \theta = \dfrac{2\pi}{m} \leqq \dfrac{2\pi}{3}$ なので
$$\begin{array}{c}
\dfrac{1}{2} \leqq \cos \dfrac{\theta}{2} \lt 1 \\
\dfrac{1}{4} \leqq \cos^2 \dfrac{\theta}{2} \lt 1
\end{array}$$であるから、$f(m)$ は収束し、
$$\begin{eqnarray}
f(m)&=&\dfrac{\pi(\theta \ – \ \sin \theta)}{\theta} \cdot \dfrac{1}{1-\cos^2 \dfrac{\theta}{2}} \\
&=& \boldsymbol{\dfrac{\pi(\theta \ – \ \sin \theta)}{\theta \sin^2 \dfrac{\theta}{2}}}
\end{eqnarray}$$

⑶

⑵より
$$f(m)=4\pi \cdot \dfrac{\theta \ – \ \sin \theta}{\theta^3} \cdot \left( \dfrac{\dfrac{\theta}{2}}{\sin \dfrac{\theta}{2}} \right)^2$$であり、$\theta = \dfrac{2\pi}{m}$ より $m \to \infty$ のとき $\theta \to 0$ なので
$$\displaystyle \lim_{ m \to \infty } f(m) = 4\pi \cdot \dfrac{1}{6} \cdot 1^2 = \boldsymbol{\dfrac{2\pi}{3}}$$

解説

図形を文章で記述している問題は長文になりがちですので、読み落としの無いよう丁寧に読み進めましょう。

また、本問のように自分で漸化式を立てる問題は難関大で定番です。$n$ と $n+1$ の状況をうまく式で関連付けましょう。交点（接点）や角度、相似比（面積比）などに注意すれば大丈夫です。

本問は誘導が丁寧にされていますが、いきなり⑶を問われても解けるようになれるとなお良いですね。

ちなみに、⑶の問題文に出てきた $\displaystyle \lim_{ x \to 0 } \dfrac{x-\sin x}{x^3} = \dfrac{1}{6}$ は、$\sin x$ のマクローリン展開に対して $5$ 次以上の項を無視した以下の式が由来となっています。
$$\sin x = x \ – \ \dfrac{1}{6}x^3$$

まとめ

今回は、神戸大学理系数学（2022年 第2問）の解説をしました。