神戸大学 理系数学 2022年 第3問 解説

今回は、神戸大学理系数学（2022年 第3問）の解説をしたいと思います。

問題

$a$ を実数，$0 \lt a \lt 1$ とし，$f(x)=\log \left( 1+x^2 \right)-ax^2$ とする．以下の問に答えよ．

⑴　関数 $f(x)$ の極値を求めよ．

⑵　$f(1)=0$ とする．曲線 $y=f(x)$ と $x$ 軸で囲まれた図形の面積を求めよ．

（神戸大学）

解答

⑴

$$\begin{eqnarray}
f'(x) &=& \dfrac{2x}{1+x^2} -2ax \\
&=& 2x \left( \dfrac{1}{1+x^2} \ – \ a \right) \\
&=& \dfrac{-2ax \left\{ x^2-\left( \dfrac{1}{a}-1 \right) \right\}}{1+x^2}
\end{eqnarray}$$

$0 \lt a \lt 1$ より $\dfrac{1}{a}-1\gt 0$ であるから、
$$f'(x)=0 \ \Longleftrightarrow \ x=0, \ \pm \sqrt{ \dfrac{1}{a}-1 }$$

よって、$f(x)$ の増減表は次のようになる。

$$\begin{array}{c|c|c|c|c|c|c|c} \hline
x & \cdots & -\sqrt{ \dfrac{1}{a}-1 } & \cdots & 0 & \cdots & \sqrt{ \dfrac{1}{a}-1 } & \cdots \\
\hline
f’(x) & + & 0 & – & 0 & + & 0 & – \\
\hline
f(x) & \nearrow & \text{極大} & \searrow & \text{極小} & \nearrow & \text{極大} & \searrow \\
\hline
\end{array}$$

よって、極大値は $f\left( \pm \sqrt{ \dfrac{1}{a}-1 } \right)= \boldsymbol{a-\log a-1}$、極小値は $f(0)=\mathbf{0}$

⑵

$f(1)=0$ より
$$\log 2-a=0 \ \Longleftrightarrow \ a=\log 2$$

ここで、$f(-x)=f(x)$ であるから、$f(x)$ は偶関数である。

また、$f(0)=f(1)=0$ と⑴の増減表より、曲線 $y=f(x)$ の概形は次のようになる。

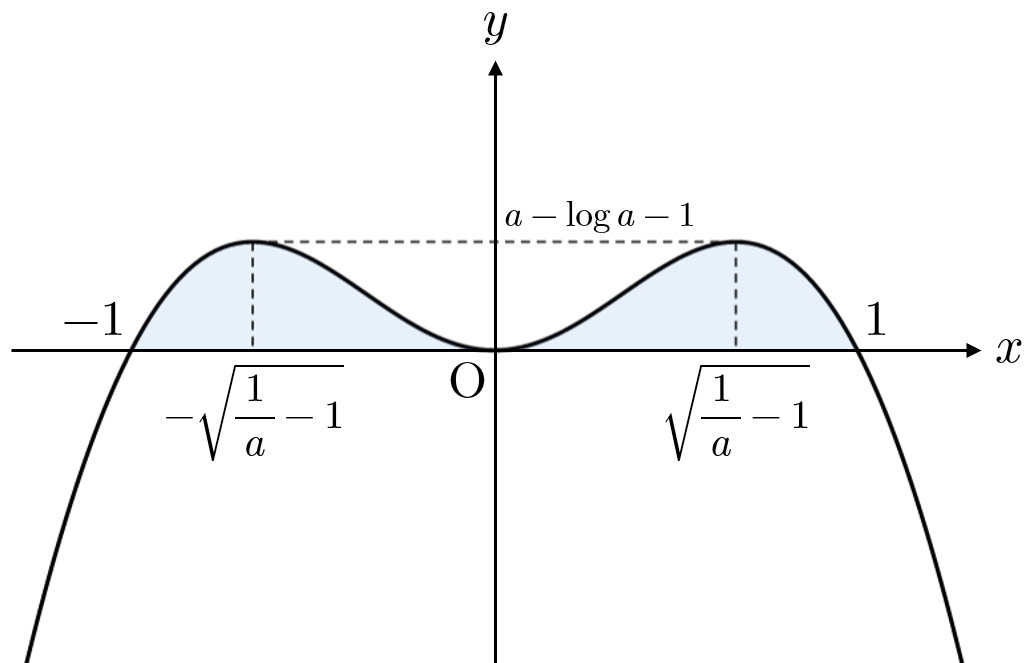
よって、求める面積を $S$ とすると
$$\begin{eqnarray}
S &=& 2\displaystyle \int_0^1 \left\{\log \left( 1+x^2 \right) – (\log 2) x^2 \right\} dx \\
\dfrac{S}{2} &=& \displaystyle \int_0^1 \log \left( 1+x^2 \right) dx \ – \ (\log 2) \displaystyle \int_0^1 x^2 dx \\
&=& \left[ x\log \left( 1+x^2 \right) \right]_0^1 \ – \displaystyle \int_0^1 x\cdot \dfrac{2x}{1+x^2} dx \ – \ (\log 2) \left[ \dfrac{1}{3}x^3 \right]_0^1 \\
&=& \log 2 \ – \ 2 \displaystyle \int_0^1 \left( 1- \dfrac{1}{1+x^2} \right) dx \ – \ \dfrac{1}{3}\log 2 \\
&=& \dfrac{2}{3}\log 2-2+2\displaystyle \int_0^1 \dfrac{1}{1+x^2} dx \\
\end{eqnarray}$$

ここで、$\displaystyle \int_0^1 \dfrac{1}{1+x^2} dx$ について $x=\tan \theta$ とおくと
$$dx=\dfrac{1}{\cos^2 \theta}d\theta \qquad
\begin{array}{c|c} \hline
x & 0 \to 1 \\
\hline
\theta & 0 \to \dfrac{\pi}{4} \\
\hline
\end{array}$$より
$$\begin{eqnarray}
\displaystyle \int_0^1 \dfrac{1}{1+x^2} dx &=& \displaystyle \int_0^\frac{\pi}{4} \dfrac{1}{1+\tan^2 \theta}\dfrac{1}{\cos^2 \theta}d\theta \\
&=& \displaystyle \int_0^\frac{\pi}{4} d\theta = \dfrac{\pi}{4}
\end{eqnarray}$$である。

よって、求める面積は
$$\begin{eqnarray}
\dfrac{S}{2} &=& \dfrac{2}{3}\log 2-2+2\cdot\dfrac{\pi}{4} \\[0.5em]
S &=& \boldsymbol{\dfrac{4}{3}\log 2+\pi-4}
\end{eqnarray}$$

解説

微積分の要点が詰まった1問です。注意したいポイントが多いので、計算ミスに注意しましょう。

まず細かいところですが、$f'(x)=0$ の解を求める際、$\sqrt{ \dfrac{1}{a}-1 }$ が実数であることを確認するため、$\dfrac{1}{a}-1 \gt 0$ を示す必要があります。
もし $\dfrac{1}{a}-1 \lt 0$ なら、$f'(x)=0$ の実数解は $x=0$ だけであり、$f(x)$ は極値を多くとも $1$ つしかもたないことになりますからね。

また、$f(x)$ が偶関数（グラフが $y$ 軸について対称）であることに気づければ、計算量を減らして計算ミスをしにくくなります。グラフで囲まれた面積を求めるときには、対称性がないかをチェックするようにしましょう。

$\displaystyle \int_0^1 \dfrac{1}{1+x^2} dx$ の積分計算は頻出なので、覚えておいた方が良いと思います。

まとめ

今回は、神戸大学理系数学（2022年 第3問）の解説をしました。