神戸大学 理系数学 2021年 第4問 解説

今回は、神戸大学理系数学（2021年 第4問）の解説をしたいと思います。

問題

$m$ を実数とする．座標平面上の放物線 $y=x^2$ と直線 $y=mx+1$ の共有点を $\mathrm{A},\mathrm{B}$ とし，原点を $\mathrm{O}$ とする．以下の問に答えよ．

⑴　$\angle\mathrm{AOB}=\dfrac{\pi}{2}$ が成り立つことを示せ．

⑵　$3$ 点 $\mathrm{A},\mathrm{B},\mathrm{O}$ を通る円の方程式を求めよ．

⑶　放物線 $y=x^2$ と⑵の円が $\mathrm{A},\mathrm{B},\mathrm{O}$ 以外の共有点をもたないような $m$ の値をすべて求めよ．

（神戸大学）

解答

⑴

$2$ 点 $\mathrm{A},\mathrm{B}$ は放物線 $y=x^2$ 上にあるので、実数 $\alpha,\beta$（ $\alpha\lt\beta$ ）を用いて、$\mathrm{A}(\alpha,\alpha^2), \ $$\mathrm{B}(\beta,\beta^2)$ とおける。

$\alpha,\beta$ は、$y=x^2$ と $y=mx+1$ から $y$ を消去した式
$$x^2-mx-1=0$$の $2$ 解なので、解と係数の関係により
$$\alpha+\beta=m,\quad\alpha\beta=-1$$が成り立つ。

ここで
$$\begin{align}
\overrightarrow{\mathrm{OA}}\cdot\overrightarrow{\mathrm{OB}}
&= \alpha\beta+\alpha^2\beta^2 \\
&= -1+(-1)^2 \\
&= 0
\end{align}$$より、$\overrightarrow{\mathrm{OA}}\perp\overrightarrow{\mathrm{OB}}$ となる。

よって、$\angle\mathrm{AOB}=\dfrac{\pi}{2}$ が成り立つ。$$\tag{証明終}$$

⑵

$\angle\mathrm{AOB}=\dfrac{\pi}{2}$ より、$3$ 点 $\mathrm{A},\mathrm{B},\mathrm{O}$ を通る円（ $C$ とする。）は、線分 $\mathrm{AB}$ を直径とする円である。

したがって、線分 $\mathrm{AB}$ の中点を $\mathrm{P}$ とすると、円 $C$ の中心は $\mathrm{P}$ となる。

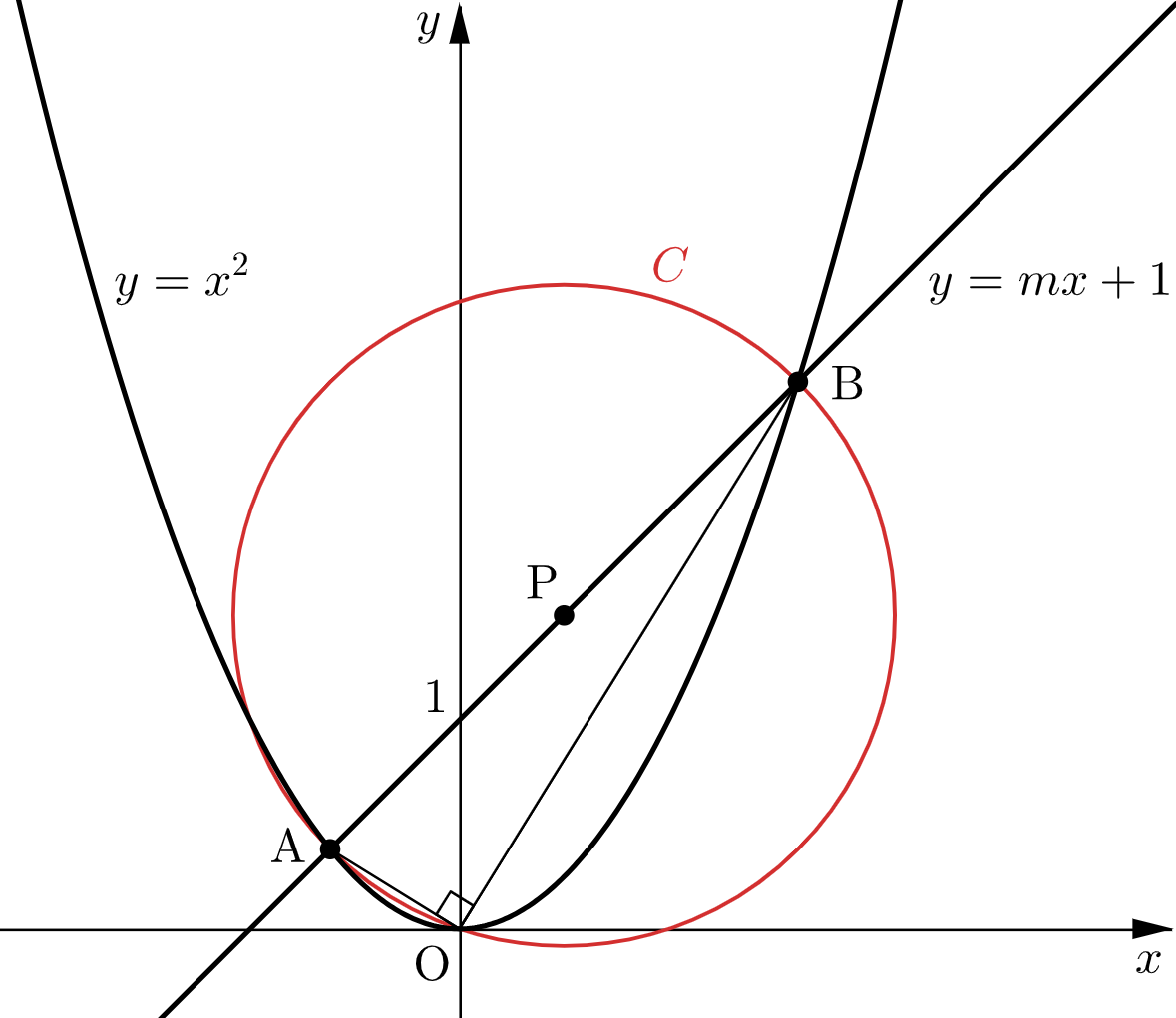
$\mathrm{P}(X,Y)$ とすると
$$\begin{align}
X &= \dfrac{\alpha+\beta}{2}=\dfrac{m}{2} \\[0.3em]
Y &= \dfrac{\alpha^2+\beta^2}{2} \\
&= \dfrac{(\alpha+\beta)^2-2\alpha\beta}{2} \\
&= \dfrac{m^2+2}{2}
\end{align}$$より、$\mathrm{P}\left(\dfrac{m}{2},\dfrac{m^2+2}{2}\right)$ である。

線分 $\mathrm{OP}$ は円 $C$ の半径なので、求める円 $C$ の方程式は
$$\begin{align}
\left(x-\dfrac{m}{2}\vphantom{\dfrac{2}{2}}\right)^2+\left(y-\dfrac{m^2+2}{2}\right)^2 &= \left(\dfrac{m}{2}\vphantom{\dfrac{2}{2}}\right)^2+\left(\dfrac{m^2+2}{2}\right)^2 \\
&= \dfrac{m^4+5m^2+4}{4}
\end{align}$$すなわち
$$\boldsymbol{\left(x-\dfrac{m}{2}\vphantom{\dfrac{2}{2}}\right)^2+\left(y-\dfrac{m^2+2}{2}\right)^2=\dfrac{(m^2+1)(m^2+4)}{4}}$$である。

⑶

円 $C$ の方程式と $y=x^2$ から $y$ を消去すると
$$\left(x-\dfrac{m}{2}\vphantom{\dfrac{2}{2}}\right)^2+\left(x^2-\dfrac{m^2+2}{2}\right)^2=\dfrac{(m^2+1)(m^2+4)}{4}$$となる。

これを展開して整理すると
$$\begin{align}
x^2-mx+x^4-(m^2+2)x^2 &= 0 \\
x\{x^3-(m^2+1)x-m\} &= 0 \\
x(x^2-mx-1)(x+m) &= 0
\end{align}$$となり、この解は
$$x=0,\alpha,\beta,-m$$である。

これら $4$ つの解は、円 $C$ と放物線 $y=x^2$ の共有点の $x$ 座標なので、題意を満たすのは $m=0,-\alpha,-\beta$ のときである。

ここで、$\alpha\lt\beta$ より
$$\alpha=\dfrac{m-\sqrt{m^2+4}}{2},\quad\beta=\dfrac{m+\sqrt{m^2+4}}{2}$$であるから、$m=-\alpha$ のとき
$$\begin{align}
m &= \dfrac{\sqrt{m^2+4}-m}{2} \\[0.3em]
\therefore \ 3m &= \sqrt{m^2+4}
\end{align}$$$m\geqq 0$ のとき、両辺を $2$ 乗して
$$\begin{align}
9m^2 &= m^2+4 \\[0.3em]
\therefore \ m &= \dfrac{1}{\sqrt{2}} \ \text{（}\because m\geqq 0 \ \text{）}
\end{align}$$

また、$m=-\beta$ のとき
$$\begin{align}
m &= \dfrac{-m-\sqrt{m^2+4}}{2} \\[0.3em]
\therefore \ -3m &= \sqrt{m^2+4}
\end{align}$$$m\leqq 0$ のとき、両辺を $2$ 乗して
$$\begin{align}
9m^2 &= m^2+4 \\[0.3em]
\therefore \ m &= -\dfrac{1}{\sqrt{2}} \ \text{（}\because m\leqq 0 \ \text{）}
\end{align}$$

以上より、求める $m$ の値は $\mathbf{0}, \ \boldsymbol{\pm\dfrac{1}{\sqrt{2}}}$ である。

解説

⑴は、$\alpha,\beta$ を具体的に求めて直線 $\mathrm{OA}$ と直線 $\mathrm{OB}$ の傾きの積が $-1$ ということを示しても良いですが、より記述をスッキリさせるために、本解答では「解と係数の関係」と「ベクトルの内積」を使いました。

⑵は、⑴をヒントとして、無駄な計算をしないように注意しましょう。

⑶のように、円と放物線の共有点について議論する際、図で考えたくなりますが、イメージとして状況が把握できるだけで、理論的に答えを求める上ではたいてい意味がありません。式の上で理論立てることを考えましょう。

$x$ の $4$ 次式の因数分解では、$x=0,\alpha,\beta$ が解となることが分かっていれば、時間短縮できます。

また、$\sqrt{\hphantom{m}\vphantom{b}}$ の入った方程式を $2$ 乗するときは、必ず両辺が $0$ 以上となっているか確認してから（あるいはそのように条件づけてから）するようにしましょう。

まとめ

今回は、神戸大学理系数学（2021年 第4問）の解説をしました。