今回は、京都大学理系数学(2019年 第4問)の解説をしたいと思います。
問題
$1$ つのさいころを $n$ 回続けて投げ,出た目を順に $X_1,X_2,\cdots,X_n$ とする。このとき次の条件をみたす確率を $n$ を用いて表せ。ただし $X_0=0$ としておく。
条件:$1\leqq k\leqq n$ をみたす $k$ のうち,$X_{k-1}\leqq4$ かつ $X_k\geqq5$ が成立するような $k$ の値はただ $1$ つである。
(京都大学)
解答
$k$ を、$1\leqq k\leqq n$ で $X_{k-1}\leqq4$ かつ $X_k\geqq5$ を満たす、ただ $1$ つの値とする。
$X_{n+1}=0$ とすると、条件を満たすとき、$k\leqq \ell\leqq n$ を満たす $\ell$ のうち、$X_{\ell}\geqq5$ かつ $X_{\ell+1}\leqq4$ が成立するような $\ell$ の値はただ $1$ つとなる。
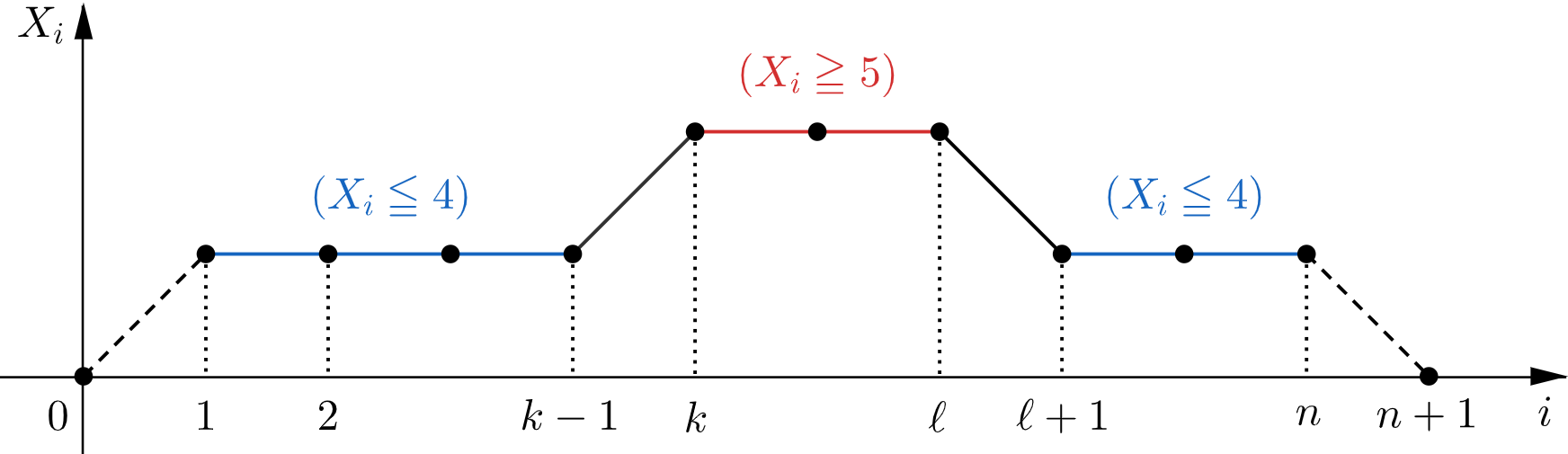
このとき、さいころの出た目は
$$\left\{\begin{alignat}{2}
&X_i\leqq4 \ \text{(}\,1\leqq i\leqq k-1\,\text{のとき)}& &\quad\cdots\text{①} \\[0.2em]
&X_i\geqq5 \ \text{(}\,k\leqq i\leqq \ell\,\text{のとき)} \\[0.2em]
&X_i\leqq4 \ \text{(}\,\ell+1\leqq i\leqq n\,\text{のとき)}& &\quad\cdots\text{②} \\
\end{alignat}\right.$$のように遷移する。
なお、$k=1$ のときは①がなく、$\ell=n$ のときは②がない。
さいころを $1$ 回投げたとき、出た目が $4$ 以下となる確率は $\dfrac{2}{3}$,$5$ 以上となる確率は $\dfrac{1}{3}$ なので、求める確率は
$$\begin{eqnarray}
&& \displaystyle\sum_{k=1}^{n}\displaystyle\sum_{\ell=k}^{n}\left(\dfrac{2}{3}\right)^{k-1}\left(\dfrac{1}{3}\right)^{\ell-k+1}\left(\dfrac{2}{3}\right)^{n-\ell} \\
&=& \dfrac{2^{n-1}}{3^n}\displaystyle\sum_{k=1}^{n}2^k\left\{\displaystyle\sum_{\ell=k}^{n}\left(\dfrac{1}{2}\right)^{\ell}\right\} \\
&=& \dfrac{2^{n-1}}{3^n}\displaystyle\sum_{k=1}^{n}2^k\cdot\dfrac{\dfrac{1}{2^k}\left(1-\dfrac{1}{2^{n-k+1}}\right)}{1-\dfrac{1}{2}} \\
&=& \dfrac{2^n}{3^n}\displaystyle\sum_{k=1}^{n}\left(1-\dfrac{1}{2^{n-k+1}}\right) \\
&=& \dfrac{1}{3^n}\displaystyle\sum_{k=1}^{n}(2^n-2^{k-1}) \\
&=& \dfrac{1}{3^n}\left(2^n\cdot n-\dfrac{2^n-1}{2-1}\right) \\[0.2em]
&=& \boldsymbol{(n-1)\left(\dfrac{2}{3}\right)^n+\left(\dfrac{1}{3}\right)^n}
\end{eqnarray}$$
$$\boldsymbol{(n-1)\left(\dfrac{2}{3}\right)^n+\left(\dfrac{1}{3}\right)^n}$$
解説
この問題には、要注意ポイントがいくつかあります。
- $1$ 回目に $5$ 以上が出た場合も、「$\,4$ 以下 → $5$ 以上」が成立すること
- 「$\,4$ 以下 → $5$ 以上」が成立した後、ずっと $5$ 以上である必要はないこと
これらのポイントを踏まえると、「$\,5$ 以上 → $4$ 以下」が成立するのは $1$ 回以下で、その後はずっと $4$ 以下でないといけない、と分かります。
本解答では、$X_{n+1}=0$ とすることで強制的に「$\,5$ 以上 → $4$ 以下」が成立するようにして、$1$ つの式で確率を求められるように工夫しました。
状況を把握する力だけでなく、等比級数や指数の計算を正確にやりきる力も求められる問題です。
まとめ
今回は、京都大学理系数学(2019年 第4問)の解説をしました。
ほかの問題にもチャレンジしよう!
京都大学 理系数学 2019年 第1問 解説
京都大学 理系数学 2019年 第2問 解説
京都大学 理系数学 2019年 第3問 解説
京都大学 理系数学 2019年 第4問 解説
京都大学 理系数学 2019年 第5問 解説
京都大学 理系数学 2019年 第6問 解説













