京都大学 理系数学 2023年 第5問 解説

今回は、京都大学理系数学（2023年 第5問）の解説をしたいと思います。

問題

　$\mathrm{O}$ を原点とする $xyz$ 空間において，点 $\mathrm{P}$ と点 $\mathrm{Q}$ は次の $3$ つの条件⒜，⒝，⒞を満たしている．

⒜　点 $\mathrm{P}$ は $x$ 軸上にある．
⒝　点 $\mathrm{Q}$ は $yz$ 平面上にある．
⒞　線分 $\mathrm{OP}$ と線分 $\mathrm{OQ}$ の長さの和は $1$ である．

点 $\mathrm{P}$ と点 $\mathrm{Q}$ が条件⒜，⒝，⒞を満たしながらくまなく動くとき，線分 $\mathrm{PQ}$ が通過してできる立体の体積を求めよ．

（京都大学）

解答

対称性より、求める体積は、点 $\mathrm{P}$ の $x$ 座標が $0$ 以上のとき線分 $\mathrm{PQ}$ が通過してできる立体の体積の $2$ 倍である。

点 $\mathrm{P}$ の座標を $(a,0,0)$（$\,0\leqq a\leqq1\,$）とすると、$\mathrm{OQ}=1-a$ となるから、点 $\mathrm{Q}$ は $yz$ 平面上で原点を中心とする半径 $1-a$ の円周上を動く。

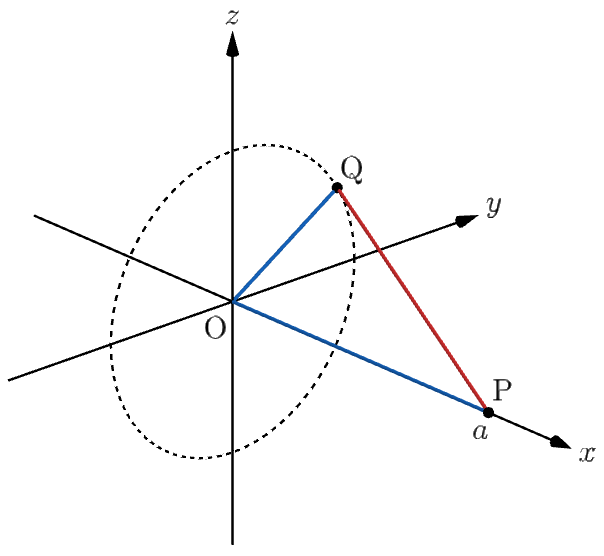
$0\leqq k\leqq 1$ とし、題意の立体を平面 $x=k$ で切ったときの断面について考える。

$xy$ 平面上で、$2$ 点 $(a,0)$，$(0,1-a)$ を通る直線の方程式は
$$\dfrac{x}{a}+\dfrac{y}{1-a}=1.\quad(0\lt a\lt1)\quad\cdots\text{①}$$

①と直線 $x=k$ の交点の $y$ 座標を $f(a)$ とすると
$$\begin{eqnarray}
\dfrac{k}{a}+\dfrac{f(a)}{1-a} &=& 1 \\
f(a) &=& (1-a)\left(1-\dfrac{k}{a}\right) \\
\therefore \ f(a) &=& k+1-a-\dfrac{k}{a}\,.
\end{eqnarray}$$

ここで、$k\leqq a\leqq1$ において $f(a)$ がとりうる値の範囲を考える。

$$f'(a)=-1+\dfrac{k}{a^2}.$$

$f'(a)=0$ の解は $a=\pm\sqrt{k}$ であるが、$k\leqq a\leqq1$ より $a=\sqrt{k}\,.$

よって、$k\leqq a\leqq1$ における $f(a)$ の増減表は次のようになる。
$$\begin{array}{c|c|c|c|c|c} \hline
a & k & \cdots & \sqrt{k} & \cdots& 1 \\ \hline
f'(a) & & + & 0 & – & \\ \hline
f(a) & 0 & \nearrow & f(\sqrt{k}\,) & \searrow & 0 \\ \hline
\end{array}$$なお $f(\sqrt{k}\,)=k-2\sqrt{k}+1.$

したがって、題意の立体を平面 $x=k$ で切ったときの断面は半径 $f(\sqrt{k}\,)$ の円（周および内部）となるので、求める体積を $V$ とすると
$$\begin{eqnarray}
V &=& 2\displaystyle\int_0^1\pi\{f(\sqrt{k}\,)\}^2dk \\
&=& 2\pi\displaystyle\int_0^1(k-2\sqrt{k}+1)^2dk \\
&=& 2\pi\displaystyle\int_0^1(k^2+6k+1-4k^{\frac{3}{2}}-4k^{\frac{1}{2}})\,dk \\[0.3em]
\dfrac{V}{2\pi} &=& \left[\dfrac{k^3}{3}+3k^2+k-4\cdot\dfrac{2}{5}k^{\frac{5}{2}}-4\cdot\dfrac{2}{3}k^{\frac{3}{2}}\right]_0^1 \\[0.2em]
&=& \dfrac{1}{3}+3+1-\dfrac{8}{5}-\dfrac{8}{3} \\[0.2em]
&=& \dfrac{1}{15} \\[0.5em]
\therefore \ V &=& \boldsymbol{\dfrac{2}{15}\pi}\,.
\end{eqnarray}$$

解説

点 $\mathrm{P}$ を固定したとき、点 $\mathrm{Q}$ は $\mathrm{OQ}=1-\mathrm{OP}$ を保ったまま動くのでその軌道は円となり、線分 $\mathrm{PQ}$ の通過する軌跡は円錐の側面となることはイメージできると思います。

問題はさらに点 $\mathrm{P}$ も動かしたときの通過立体の体積ですが、この立体は $x$ 軸を中心軸とする回転体なので、$x$ 軸に垂直に切った断面積を積分すると良いです。

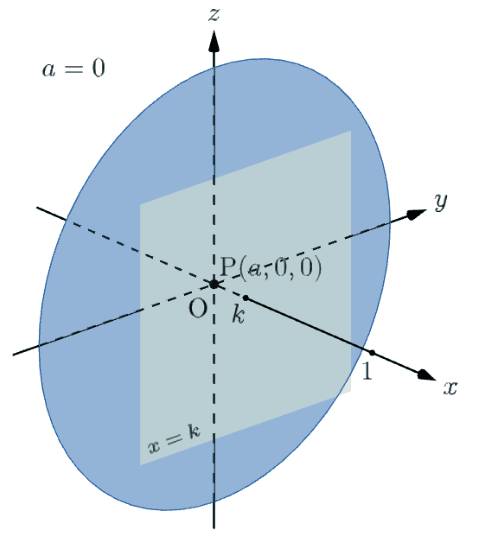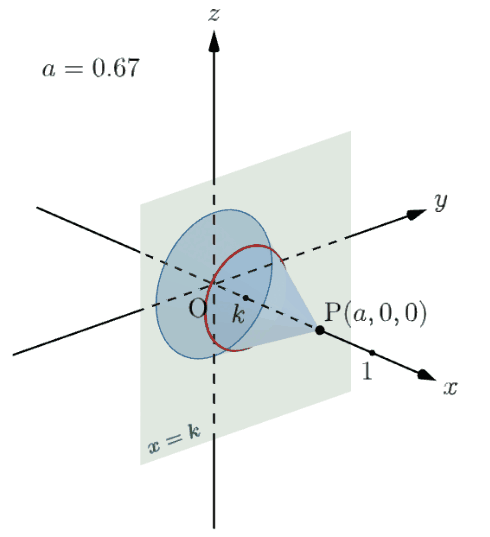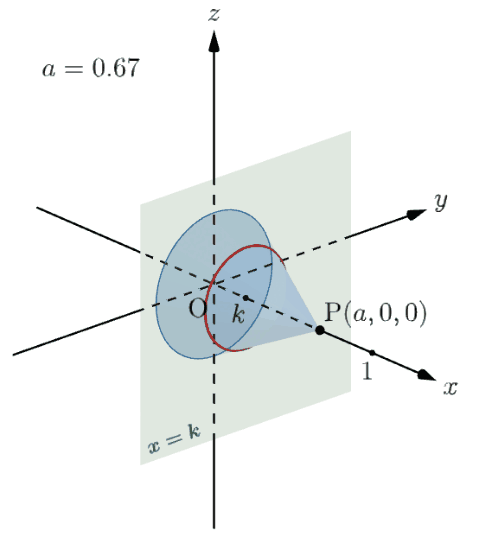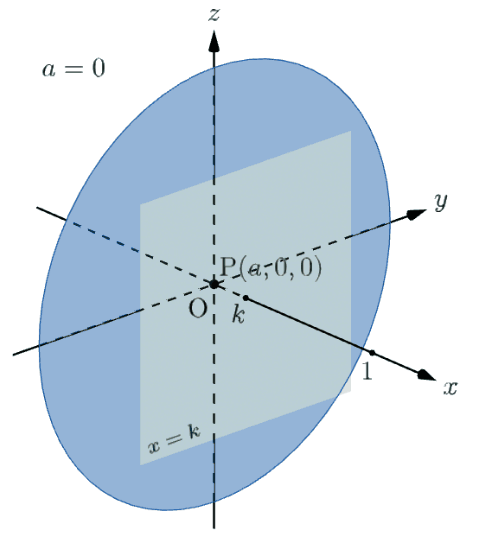
下のアニメーションを見ると、題意の立体の平面 $x=k$ による断面（赤い円）は $k\leqq a\leqq1$ の範囲でしか存在せず、その半径は $0$ から極大値までのすべての値をとることが分かると思います。この極大値が $f(\sqrt{k}\,)$ なので、題意の立体の平面 $x=k$ による断面の面積は $\pi\{f(\sqrt{k}\,)\}^2$ で求められるというわけです。

まとめ

今回は、京都大学理系数学（2023年 第5問）の解説をしました。