神戸大学 理系数学 2021年 第5問 解説

今回は、神戸大学理系数学（2021年 第5問）の解説をしたいと思います。

問題

座標平面上を運動する点 $\mathrm{P}(x,y)$ の時刻 $t$ における座標が
$$x=\dfrac{4+5\cos t}{5+4\cos t},\quad y=\dfrac{3\sin t}{5+4\cos t}$$であるとき，以下の問に答えよ．

⑴　点 $\mathrm{P}$ と原点 $\mathrm{O}$ との距離を求めよ．

⑵　点 $\mathrm{P}$ の時刻 $t$ における速度 $\overrightarrow{\vphantom{b}v}=\left(\dfrac{dx}{dt},\dfrac{dy}{dt}\right)$ と速さ $| \ \overrightarrow{\vphantom{b}v} \ |$ を求めよ．

⑶　定積分 $\displaystyle\int_0^\pi\dfrac{dt}{5+4\cos t}$ を求めよ．

（神戸大学）

解答

⑴

$$\begin{align}
\mathrm{OP} &= \sqrt{\left(\dfrac{4+5\cos t}{5+4\cos t}\right)^2+\left(\dfrac{3\sin t}{5+4\cos t}\right)^2} \\
&= \sqrt{\dfrac{16+40\cos t+25\cos^2t+9\sin^2t}{(5+4\cos t)^2}} \\
&= \sqrt{\dfrac{25+40\cos t+16\cos^2t}{(5+4\cos t)^2}} \\
&= \sqrt{\dfrac{(5+4\cos t)^2}{(5+4\cos t)^2}} \\[0.3em]
&= \mathbf{1}
\end{align}$$

⑵

$$\begin{align}
\dfrac{dx}{dt} &= \dfrac{-5\sin t(5+4\cos t)-(4+5\cos t)(-4\sin t)}{(5+4\cos t)^2} \\
&= \dfrac{-9\sin t}{(5+4\cos t)^2}\\[0.5em]
\dfrac{dy}{dt} &= \dfrac{3\cos t(5+4\cos t)-3\sin t(-4\sin t)}{(5+4\cos t)^2} \\
&= \dfrac{12+15\cos t}{(5+4\cos t)^2}
\end{align}$$より
$$\overrightarrow{\vphantom{b}v}=\boldsymbol{\left(\dfrac{-9\sin t}{(5+4\cos t)^2}\right.}, \ \boldsymbol{\left.\dfrac{12+15\cos t}{(5+4\cos t)^2}\right)}$$

さらに
$$\overrightarrow{\vphantom{b}v}=\dfrac{3}{(5+4\cos t)^2}(-3\sin t, \ 4+5\cos t)$$より
$$\begin{align}
| \ \overrightarrow{\vphantom{b}v} \ |
&= \dfrac{3}{(5+4\cos t)^2}\sqrt{(-3\sin t)^2+(4+5\cos t)^2} \\
&= \dfrac{3}{(5+4\cos t)^2}\sqrt{9\sin^2t+16+40\cos t+25\cos^2t} \\
&= \dfrac{3}{(5+4\cos t)^2}\sqrt{25+40\cos t+16\cos^2t} \\
&= \dfrac{3}{(5+4\cos t)^2}\sqrt{(5+4\cos t)^2} \\
&= \dfrac{3}{(5+4\cos t)^2}\cdot(5+4\cos t) \\
&\hphantom{=} \ \text{（}\because -1\leqq\cos t\leqq 1 \ \text{より} \ 5+4\cos t\gt 0 \ \text{）} \\[0.3em]
&= \boldsymbol{\dfrac{3}{5+4\cos t}}
\end{align}$$

⑶

⑴より $\mathrm{OP}=1$ であり、$0\leqq t\leqq\pi$ において
$$y=\dfrac{3\sin t}{5+4\cos t}\geqq 0$$であるから、点 $\mathrm{P}$ は原点を中心とする半径 $1$ の円の $y\geqq 0$ の部分に存在する。

また、$t=0$ のとき $\mathrm{P}(1,0)$，$t=\pi$ のとき $\mathrm{P}(-1,0)$ である。

さらに、$0\leqq t\leqq\pi$ において
$$\dfrac{dx}{dt}=\dfrac{-9\sin t}{(5+4\cos t)^2}\leqq 0$$より、点 $\mathrm{P}$ の $x$ 座標は単調減少する。

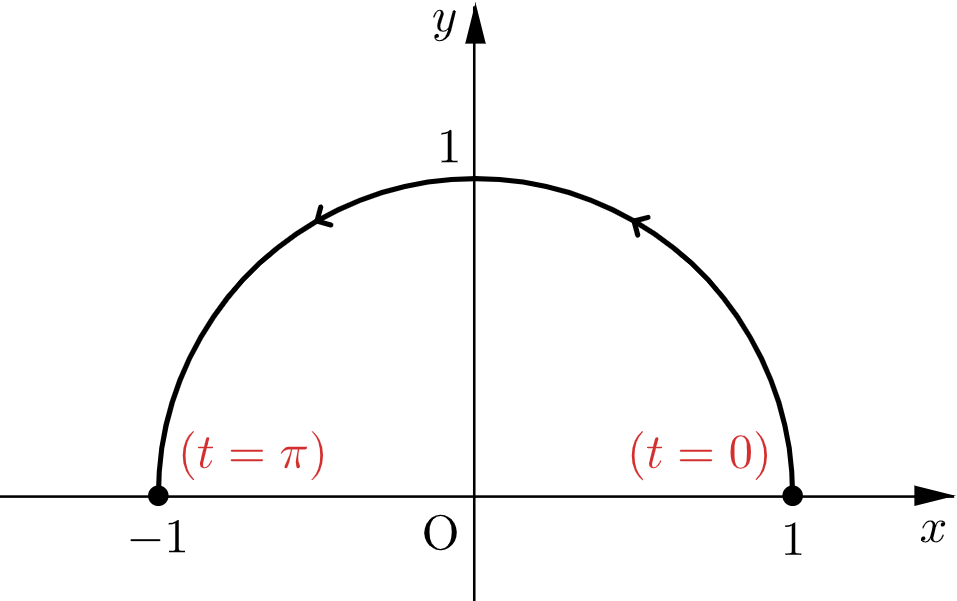
したがって、$0\leqq t\leqq\pi$ において点 $\mathrm{P}$ は半径 $1$ の円の半分を動くから、その移動距離は $\pi$ である。

また、この移動距離は $\displaystyle\int_0^\pi| \ \overrightarrow{\vphantom{b}v} \ |dt$ と表される。

よって
$$\begin{align}
\displaystyle\int_0^\pi\dfrac{dt}{5+4\cos t}
&= \dfrac{1}{3}\displaystyle\int_0^\pi\dfrac{3}{5+4\cos t}dt \\
&= \dfrac{1}{3}\displaystyle\int_0^\pi| \ \overrightarrow{\vphantom{b}v} \ |dt \\
&= \boldsymbol{\dfrac{\pi}{3}}
\end{align}$$

解説

「速度」や「速さ」という、あまり見かけない単語が並んでいますが、ふたを開けてみれば微分と三平方の定理をからめた問題だと分かります。

⑶は、⑴,⑵の利用の仕方がポイントになる問題で、物理っぽい感覚も必要となる面白い問題です。

点 $\mathrm{P}$ の移動距離が $\displaystyle\int_0^\pi| \ \overrightarrow{\vphantom{b}v} \ |dt$ と表される理由を感覚的に説明すると、速さに微小時間をかけると微小距離になり、それを積分することで総移動距離が求められるためです。

まとめ

今回は、神戸大学理系数学（2021年 第5問）の解説をしました。