大阪大学 理系数学 2020年 第3問 解説

今回は、大阪大学理系数学（2020年 第3問）の解説をしたいと思います。

問題

　$n$ を $2$ 以上の自然数とする．三角形 $\mathrm{ABC}$ において，辺 $\mathrm{AB}$ の長さを $c$，辺 $\mathrm{CA}$ の長さを $b$ で表す．$\angle\mathrm{ACB}=n\angle\mathrm{ABC}$ であるとき，$c\lt nb$ を示せ．

（大阪大学）

解答

$\angle\mathrm{ABC}=\theta$ とおくと、$\angle\mathrm{ACB}=n\theta$ である。

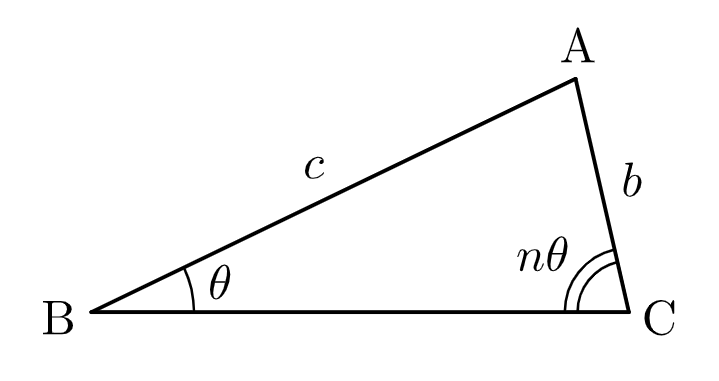
$\theta$ のとりうる範囲は、$0\lt\angle\mathrm{BAC}\lt\pi$ より
$$\begin{align}
0 &\lt \pi-(n+1)\theta\lt\pi \\[0.3em]
\therefore \ 0 &\lt \theta\lt\dfrac{\pi}{n+1} \quad\cdots\text{①}
\end{align}$$となる。

また、正弦定理により
$$\begin{align}
\dfrac{c}{\sin n\theta} &= \dfrac{b}{\sin\theta} \\[0.3em]
\therefore \ c &= \dfrac{\sin n\theta}{\sin\theta}b \quad\cdots\text{②}
\end{align}$$が成り立つ。

ここで
$$n\sin\theta-\sin n\theta\gt0 \quad\cdots(*)$$が成り立つことを示す。

$f(\theta)=n\sin\theta-\sin n\theta$ とおくと
$$\begin{align}
f'(\theta) &= n\cos\theta-n\cos n\theta \\
&= n(\cos\theta-\cos n\theta) \\
\therefore \ f'(\theta) &= 2n\sin\dfrac{(n+1)\theta}{2}\sin\dfrac{(n-1)\theta}{2}
\end{align}$$となり、①より
$$\begin{align}
0 &\lt\dfrac{(n+1)\theta}{2}\lt\dfrac{\pi}{n+1}\cdot\dfrac{(n+1)\theta}{2}=\dfrac{\pi}{2}, \\
0 &\lt\dfrac{(n-1)\theta}{2}\lt\dfrac{\pi}{n+1}\cdot\dfrac{(n-1)\theta}{2}\lt\dfrac{\pi}{2}
\end{align}$$であるから $f'(\theta)\gt0$ となる。

したがって、$f(\theta)$ は単調増加し
$$f(\theta)\gt f(0)=0$$となるから、$(*)$ が成り立つ。

③より $\sin\theta\gt0$ であるから、②と $(*)$ より
$$\begin{align}
c &= \dfrac{\sin n\theta}{\sin\theta}b \\
&\lt \dfrac{n\sin\theta}{\sin\theta}b \\[0.2em]
&= nb
\end{align}$$となるため、題意は示された。$$\tag{証明終}$$

別解

※ $(*)$ が成り立つことを、数学的帰納法により示します。

(ⅰ)　$n=2$ のとき

①より
$$0\lt\theta\lt\dfrac{\pi}{3} \quad\cdots\text{③}$$となり$$\begin{eqnarray}
&& 2\sin\theta-\sin2\theta \\
&=& 2\sin\theta-2\sin\theta\cos\theta \\
&=& 2\sin\theta(1-\cos\theta) \\
&\gt& 0 \ \text{（}\because\text{③）}
\end{eqnarray}$$より成り立つ。

(ⅱ)　$n=k$（ $k=2,3,\cdots$ ）のとき $(*)$ が成り立つ、すなわち
$$k\sin\theta\gt\sin k\theta$$が成り立つと仮定すると、$n=k+1$ のとき、①より
$$\begin{alignat}{2}
0 &\lt \theta\lt\dfrac{\pi}{k+2} \ \left(\leqq\dfrac{\pi}{3}\right)& &\quad\cdots\text{④} \\
0 &\lt k\theta\lt\dfrac{k\pi}{k+2} \ (\lt\pi)& &\quad\cdots\text{⑤}
\end{alignat}$$となり
$$\begin{eqnarray}
&& (k+1)\sin\theta-\sin(k+1)\theta \\
&=& k\sin\theta+\sin\theta-\sin k\theta\cos\theta-\cos k\theta\sin\theta \\
&\gt& \sin k\theta+\sin\theta-\sin k\theta\cos\theta-\cos k\theta\sin\theta \\
&=& \sin k\theta(1-\cos\theta)+\sin\theta(1-\cos k\theta) \\
&\gt& 0 \ \text{（}\because\text{④,⑤）}
\end{eqnarray}$$より成り立つ。

(ⅰ),(ⅱ)より、$2$ 以上の自然数 $n$ に対して $(*)$ が成り立つことが示された。

解説

状況は分かりやすく、三角形の辺と角度に関する問題なので、使える定理や式も限られてきます。

角と対辺がセットになっていることから正弦定理を使おうというのが自然な発想です。

最大の山場は $(*)$ を示すところで、$n$ が自然数という条件から数学的帰納法を用いる解法がまず思いつきます。

もちろんその解法でも解けます（別解）が、微分を使う方（本解答）がよりシンプルです。

まとめ

今回は、大阪大学理系数学（2020年 第3問）の解説をしました。