大阪大学 理系数学 2020年 第2問 解説

今回は、大阪大学理系数学（2020年 第2問）の解説をしたいと思います。

問題

　$1$ 個のさいころを $n$ 回投げて，$k$ 回目に出た目が $1$ の場合は $X_k=1$，出た目が $2$ の場合は $X_k=-1$，その他の目が出た場合は $X_k=0$ とする．
$$Y_k=\cos\left(\dfrac{\pi}{3}X_k\right)+i\sin\left(\dfrac{\pi}{3}X_k\right)$$とおき，$Y_1$ から $Y_n$ までの積 $Y_1\,Y_2\,Y_3\,\cdots Y_n$ を $Z_n$ で表す．ただし，$i$ は虚数単位とする．以下の問いに答えよ．

⑴　$Z_2$ が実数でない確率を求めよ．

⑵　$Z_1, \ Z_2, \ Z_3, \ \cdots, \ Z_n$ がいずれも実数でない確率を求めよ．

⑶　$Z_n$ が実数となる確率を $p_n$ とする．$p_n$ を $n$ を用いて表し，極限 $\displaystyle\lim_{n\to\infty}p_n$ を求めよ．

（大阪大学）

解答

⑴

$$\begin{align}
Z_2 &= Y_1\,Y_2 \\
&= \cos\left\{\dfrac{\pi}{3}(X_1+X_2)\right\}+i\sin\left\{\dfrac{\pi}{3}(X_1+X_2)\right\}
\end{align}$$$-2\leqq X_1+X_2\leqq2$ より、$Z_2$ が実数でないのは
$$X_1+X_2\ne0$$すなわち
$$(X_1,X_2)=(1,1),(1,0),(-1,-1),(-1,0),(0,1),(0,-1)$$のときである。

$X_k=1,-1,0$ となる確率はそれぞれ $\dfrac{1}{6},\dfrac{1}{6},\dfrac{4}{6}$ であるから、求める確率は
$$\dfrac{1}{6}\cdot\left(\dfrac{1}{6}+\dfrac{4}{6}\right)\cdot2+\dfrac{4}{6}\cdot\dfrac{1}{6}\cdot2=\boldsymbol{\dfrac{1}{2}}$$

⑵

$$\begin{align}
Z_n &= Y_1\,Y_2\,Y_3\,\cdots Y_n \\[0.3em]
&= \cos\left\{\dfrac{\pi}{3}(X_1+X_2+\cdots+X_n)\right\} \\
&\hphantom{=} \ +i\sin\left\{\dfrac{\pi}{3}(X_1+X_2+\cdots+X_n)\right\}
\end{align}$$より、複素数平面上で $Z_1,Z_2,\cdots,Z_n$ が表す点は、下図のように半径 $1$ の円に内接する正六角形の頂点のいずれかである。

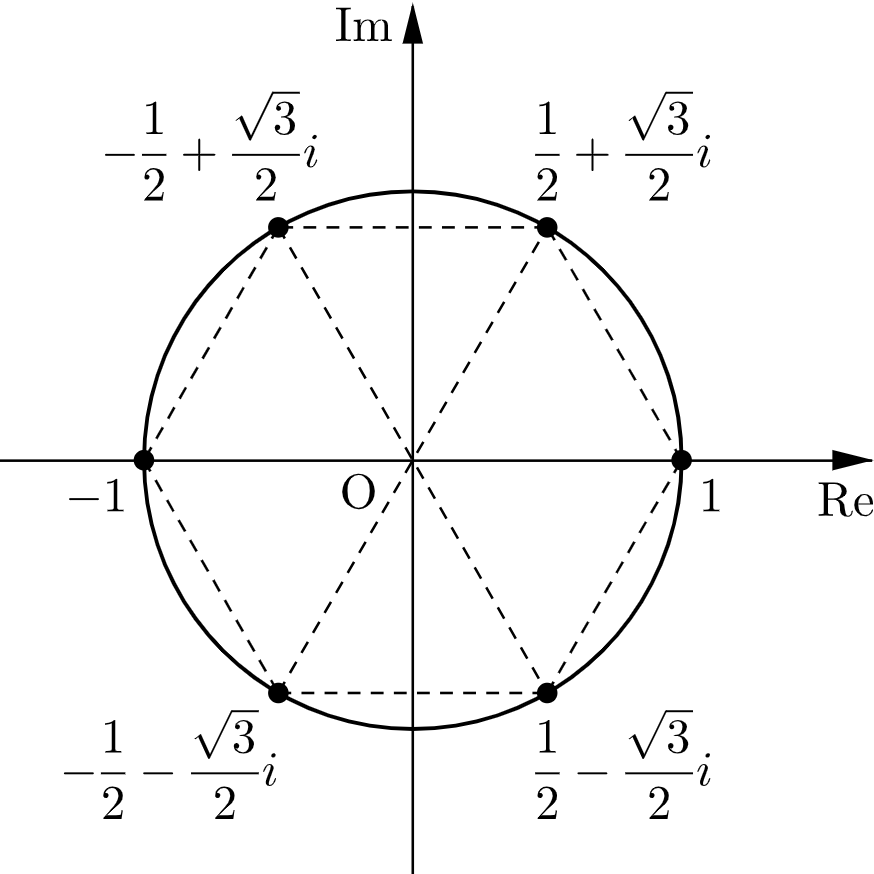
$Z_{k+1}$ が表す点について、$Z_k$ が表す点と同じである確率は $\dfrac{2}{3}$ であり、$Z_k$ が表す点の隣の点$\Big($原点を中心に $\pm\dfrac{\pi}{3}$ 回転した点$\Big)$ に移る確率は $\dfrac{1}{3}$ である。

ここで、求める確率を $q_n$ とおくと、$Z_1$ が実数でないのは $X_1=1,-1$ のときであるから
$$q_1=\dfrac{1}{6}\cdot2=\dfrac{1}{3}\quad\cdots\text{①}$$である。

$j$ を $1\leqq j\leqq n-1$ を満たす整数とすると、$Z_j$ が実数でないのは $X_1+X_2+\cdots+X_j\equiv1,2\pmod{3}$ のときである。

(ⅰ)　$X_1+X_2+\cdots+X_j\equiv1\pmod{3}$ のとき
$Z_{j+1}$ が実数でないのは $X_{j+1}=0,1$ のときであり、その確率は
$$\dfrac{4}{6}+\dfrac{1}{6}=\dfrac{5}{6}$$である。

(ⅱ)　$X_1+X_2+\cdots+X_j\equiv2\pmod{3}$ のとき
$Z_{j+1}$ が実数でないのは $X_{j+1}=0,-1$ のときであり、その確率は
$$\dfrac{4}{6}+\dfrac{1}{6}=\dfrac{5}{6}$$である。

(ⅰ),(ⅱ)より、$X_j$ が実数でないとき $X_{j+1}$ も実数でない確率は $\dfrac{5}{6}$ であるから
$$q_{j+1}=\dfrac{5}{6}q_{j}$$が成り立つ。

したがって
$$\begin{align}
q_n &= q_1\left(\dfrac{5}{6}\right)^{n-1} \\
&= \boldsymbol{\dfrac{1}{3}\cdot\left(\dfrac{5}{6}\right)^{n-1}} \ \text{（}\because\text{①）}
\end{align}$$

⑶

$Z_n$ が実数であるとき、⑵の図の $6$ 点のうち実軸上の $2$ 点のいずれかにあるので、$Z_{n+1}$ が実数となる確率は $\dfrac{2}{3}$ である。

$Z_n$ が実数でないとき、⑵の図の $6$ 点のうち実軸上にない $4$ 点のいずれかにあるので、$Z_{n+1}$ が実数となる確率は $\dfrac{1}{6}$ である。

よって
$$p_{n+1}=\dfrac{2}{3}p_n+\dfrac{1}{6}(1-p_n)$$
が成り立ち、これより
$$\begin{align}
p_{n+1} &= \dfrac{1}{2}p_n+\dfrac{1}{6} \\[0.3em]
\therefore \ p_{n+1}-\dfrac{1}{3} &= \dfrac{1}{2}\left(p_n-\dfrac{1}{3}\right)
\end{align}$$となる。

$Z_1$ が実数となるのは $X_1=0$ のときであり、その確率（ $p_1$ ）は $\dfrac{2}{3}$ であるから
$$\begin{align}
p_n-\dfrac{1}{3} &= \left(p_1-\dfrac{1}{3}\right)\cdot\left(\dfrac{1}{2}\right)^{n-1} \\[0.3em]
\therefore \ p_n &= \left(\dfrac{2}{3}-\dfrac{1}{3}\right)\cdot\left(\dfrac{1}{2}\right)^{n-1}+\dfrac{1}{3} \\
&= \boldsymbol{\dfrac{1}{3}\left\{1+\left(\dfrac{1}{2}\right)^{n-1}\right\}} \\[0.6em]
\displaystyle\lim_{n\to\infty}p_n &= \boldsymbol{\dfrac{1}{3}}
\end{align}$$

解説

さいころを $1$ 回投げるごとに複素数平面上の点が動く（もしくは留まる）ことに気づけばスムーズに解くことができます。

$X_1+X_2+\cdots+X_j$ が $3$ の倍数のとき、$Z_j$ は実数になることがポイントです。

まとめ

今回は、大阪大学理系数学（2020年 第2問）の解説をしました。