大阪大学 理系数学 2020年 第5問 解説

今回は、大阪大学理系数学（2020年 第5問）の解説をしたいと思います。

問題

　$3$ 辺の長さの和が $2$ である三角形 $\mathrm{ABC}$ において，辺 $\mathrm{BC}$ の長さを $a$，辺 $\mathrm{CA}$ の長さを $b$ で表す．三角形 $\mathrm{ABC}$ を辺 $\mathrm{BC}$ を軸として $1$ 回転させてできる回転体の体積を $V$ とする．以下の問いに答えよ．

⑴　$a$ の値を固定して $b$ の値を変化させるとき，$V$ が最大になるのは，三角形 $\mathrm{ABC}$ が辺 $\mathrm{BC}$ を底辺とする二等辺三角形となるときである．これを示せ．

⑵　$a, \ b$ の値をともに変化させるとき，$V$ の最大値と，最大値を与える $a, \ b$ の値をそれぞれ求めよ．

（大阪大学）

解答

⑴

$\mathrm{AB}=c$ とおくと、三角形の成立条件より
$$|b-c|\lt a\lt b+c$$が成り立ち、$a+b+c=2$ より
$$\begin{align}
&|a+2b-2|\lt a\lt2-a \\[0.3em]
\Longleftrightarrow \ &\left\{
\begin{aligned}
&-a\lt a+2b-2\lt a \\
&a\lt2-a
\end{aligned}
\right. \\[0.3em]
\Longleftrightarrow \ &\left\{
\begin{aligned}
&1-a\lt b\lt1 \\
&0\lt a\lt1
\end{aligned}
\right. \quad\cdots\text{①}
\end{align}$$

ここで、頂点 $\mathrm{A}$ から直線 $\mathrm{BC}$ に下ろした垂線の足を $\mathrm{H}$ とし、$\mathrm{AH}=h$ とおく。

(ⅰ)　点 $\mathrm{H}$ が辺 $\mathrm{BC}$ 上にあるとき

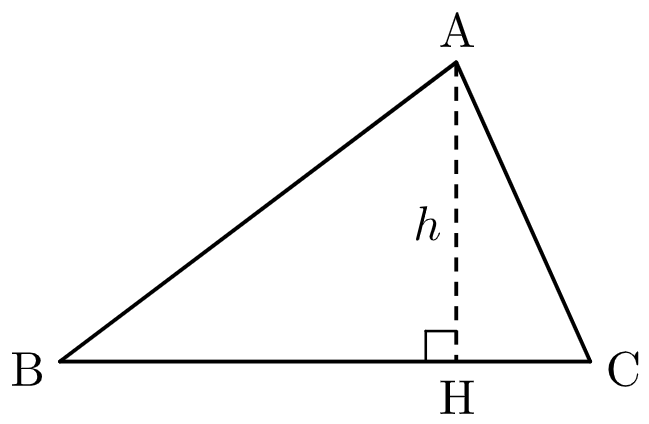
$$\begin{align}
V &= \dfrac{1}{3}\pi h^2\cdot\mathrm{BH}+\dfrac{1}{3}\pi h^2\cdot\mathrm{CH} \\
&= \dfrac{1}{3}\pi h^2\cdot(\mathrm{BH}+\mathrm{CH}) \\
&= \dfrac{1}{3}\pi h^2a
\end{align}$$

(ⅱ)　点 $\mathrm{H}$ が辺 $\mathrm{BC}$ 上にないとき

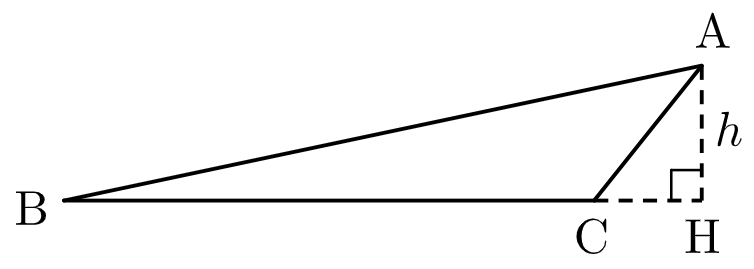
$$\begin{align}
V &= \left|\dfrac{1}{3}\pi h^2\cdot\mathrm{BH}-\dfrac{1}{3}\pi h^2\cdot\mathrm{CH}\right| \\
&= \dfrac{1}{3}\pi h^2\cdot|\mathrm{BH}-\mathrm{CH}| \\
&= \dfrac{1}{3}\pi h^2a
\end{align}$$

(ⅰ),(ⅱ)より、$V=\dfrac{1}{3}\pi h^2a$ であるから、$V$ が最大になるのは $h$ が最大になるときである。

ところで、$\mathrm{AB}+\mathrm{AC}=2-a$ で一定であるから、点 $\mathrm{A}$ は $2$ 点 $\mathrm{B},\,\mathrm{C}$ を焦点とする楕円上に存在する。

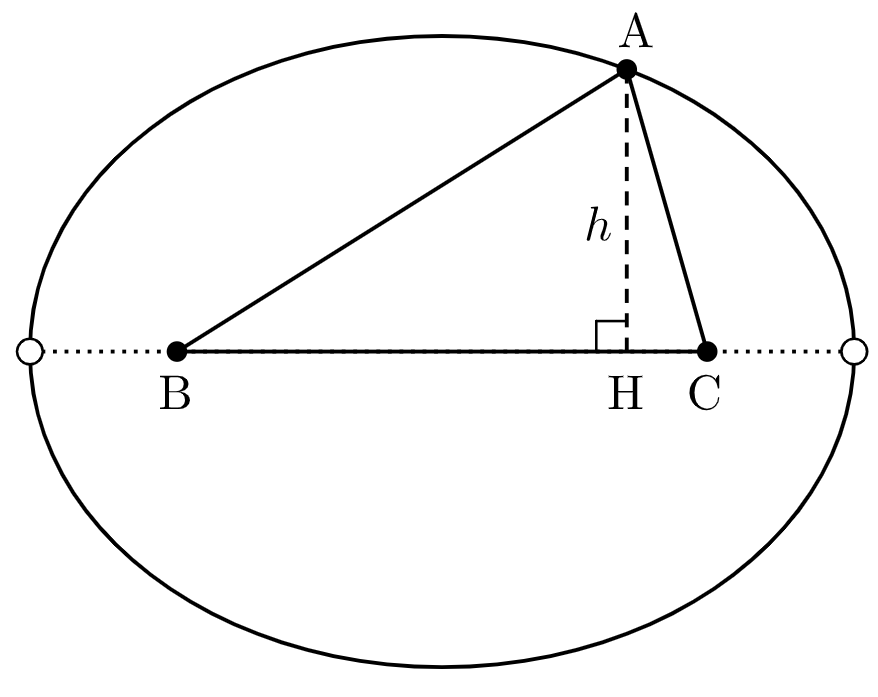
上図より、$h$ が最大になるのは $\mathrm{H}$ が辺 $\mathrm{BC}$ の中点に一致するときであり、このとき $\triangle\mathrm{ABC}$ は辺 $\mathrm{BC}$ を底辺とする二等辺三角形となる。

このとき、$a+2b=2$ より
$$b=1-\dfrac{a}{2} \quad\cdots\text{②}$$となるので①を満たす。

以上より、$V$ が最大になるのは、$\triangle\mathrm{ABC}$ が辺 $\mathrm{BC}$ を底辺とする二等辺三角形となるときである。$$\tag{証明終}$$

⑵

⑴より、$\triangle\mathrm{ABC}$ が辺 $\mathrm{BC}$ を底辺とする二等辺三角形であるときを考えると、②より
$$\begin{align}
h &= \sqrt{\left(1-\dfrac{a}{2}\right)^2-\left(\dfrac{a}{2}\right)^2} \\[0.3em]
&= \sqrt{1-a}
\end{align}$$となるので、⑴より
$$\begin{align}
V &= \dfrac{1}{3}\pi h^2a \\
&= \dfrac{1}{3}\pi(1-a)a \\
&= \dfrac{1}{3}\pi\left\{-\left(a-\dfrac{1}{2}\right)^2+\dfrac{1}{4}\right\}
\end{align}$$となり、①に注意すると、$V$ は $a=\boldsymbol{\dfrac{1}{2}}$ のとき最大値 $\boldsymbol{\dfrac{\pi}{12}}$ をとる。

このとき、②より $b=\boldsymbol{\dfrac{3}{4}}$ である。

解説

⑴は、$a$ の値を固定すると点 $\mathrm{A}$ の軌跡が楕円になることに気付けるかがポイントです。

楕円の方程式を求めて、計算によって $h$ が最大になるタイミングを議論してももちろん良いですが、点 $\mathrm{A}$ が楕円の短軸上にあるときそうなるのは明らかなので、この部分に関しては解答のように文章での説明で十分だと思います。

⑵は、⑴の誘導を活かして、$2$ 次関数の最大を考える基本的な問題です。
放物線の軸が定義域に入っているかどうかを必ず確認するようにしましょう。

まとめ

今回は、大阪大学理系数学（2020年 第5問）の解説をしました。