大阪大学 理系数学 2021年 第1問 解説

今回は、大阪大学理系数学（2021年 第1問）の解説をしたいと思います。

問題

　$a,b$ を $ab\lt 1$ をみたす正の実数とする．$xy$ 平面上の点 $\mathrm{P}(a,b)$ から，曲線 $y=\dfrac{1}{x}(x\gt 0)$ に $2$ 本の接線を引き，その接点を $\mathrm{Q}\bigg(s,\dfrac{1}{s}\bigg), \ $$\mathrm{R}\bigg(t,\dfrac{1}{t}\bigg)$ とする．ただし，$s\lt t$ とする．

⑴　$s$ および $t$ を $a,b$ を用いて表せ．

⑵　点 $\mathrm{P}(a,b)$ が曲線 $y=\dfrac{9}{4}-3x^2$ 上の $x\gt 0, \ y\gt 0$ をみたす部分を動くとき，$\dfrac{t}{s}$ の最小値とそのときの $a,b$ の値を求めよ．

（大阪大学）

解答

⑴

$a\gt 0$ より
$$ab\lt 1\quad\Longleftrightarrow\quad b\lt\dfrac{1}{a}$$であるから、点 $\mathrm{P}$ は $x\gt 0, \ 0\lt y \lt \dfrac{1}{x}$ の部分に存在する。

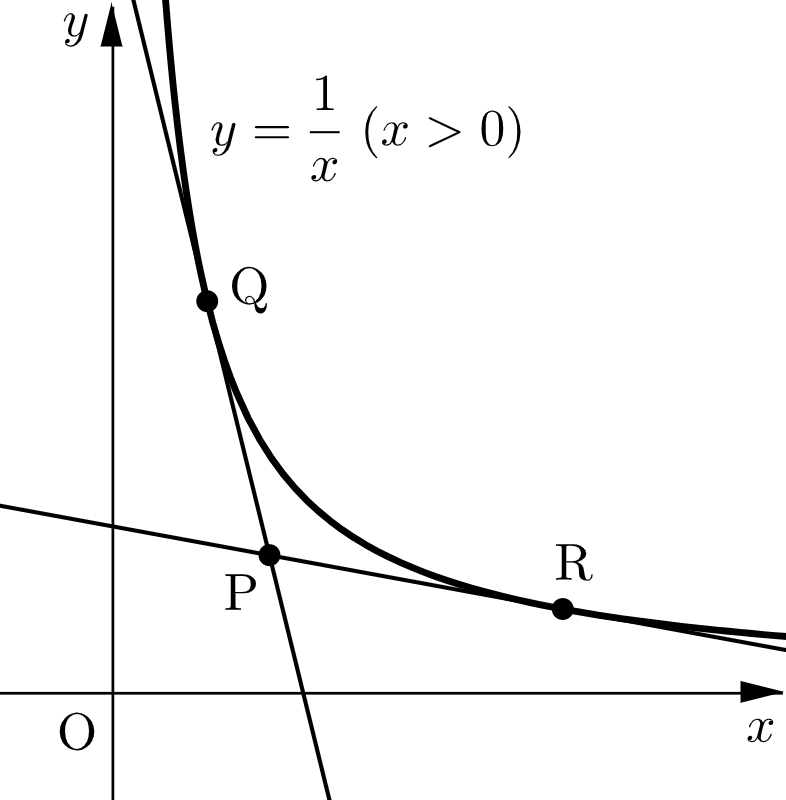
$y=\dfrac{1}{x}$ より $y’=-\dfrac{1}{x^2}$ なので、$x=u$ における曲線 $y=\dfrac{1}{x}$ の接線の方程式は
$$y=-\dfrac{1}{u^2}(x-u)+\dfrac{1}{u}$$となる。

これが点 $\mathrm{P}(a,b)$ を通るとき
$$\begin{array}{c}
b = -\dfrac{1}{u^2}(a-u)+\dfrac{1}{u} \\
\therefore\quad bu^2-2u+a = 0
\end{array}$$$b\ne 0$ より
$$u=\dfrac{1\pm\sqrt{1-ab}}{b}$$この $2$ 解が $s,t$ なので、$s\lt t$ に注意して
$$s=\boldsymbol{\dfrac{1-\sqrt{1-ab}}{b}},\quad t=\boldsymbol{\dfrac{1+\sqrt{1-ab}}{b}}$$

⑵

$$\begin{eqnarray}
\dfrac{t}{s} &=& \dfrac{1+\sqrt{1-ab}}{1-\sqrt{1-ab}} \\
&=& -1+\dfrac{2}{1-\sqrt{1-ab}} \quad\cdots\text{①}
\end{eqnarray}$$より、$\dfrac{t}{s}$ が最小となるのは $ab$ が最大となるときである。

点 $\mathrm{P}(a,b)$ は曲線 $y=\dfrac{9}{4}-3x^2$ 上の点なので
$$\begin{eqnarray}
b &=& \dfrac{9}{4}-3a^2 \quad\cdots\text{②} \\
\therefore\quad ab &=& \dfrac{9}{4}a-3a^3 \quad\cdots\text{③}
\end{eqnarray}$$

また、$b\gt 0$ より
$$\begin{eqnarray}
\dfrac{9}{4}-3a^2 \gt 0 \quad &\Longleftrightarrow& \quad a^2 \lt \dfrac{3}{4} \\
&\Longleftrightarrow& \quad -\dfrac{\sqrt{3}}{2} \lt a \lt \dfrac{\sqrt{3}}{2}
\end{eqnarray}$$$a\gt 0$ と合わせて
$$0 \lt a \lt \dfrac{\sqrt{3}}{2} \quad\cdots\text{④}$$

②の右辺を $f(a)$ とおくと
$$f'(a) = \dfrac{9}{4}-9a^2 = -9\left(a+\dfrac{1}{2}\right)\left(a-\dfrac{1}{2}\right)$$より、④における $f(a)$ の増減表は次のようになる。
$$\begin{array}{c||c|c|c|c|c}\hline
a & (0) & \cdots & \dfrac{1}{2} & \cdots & \bigg(\dfrac{\sqrt{3}}{2}\bigg) \\ \hline
f'(a) & & + & 0 & – & \\ \hline
f(a) & (0) & \nearrow & \text{最大} & \searrow & (0) \\ \hline
\end{array}$$

よって $f(a)$ は $a=\boldsymbol{\dfrac{1}{2}}$ で最大値 $f\left(\dfrac{1}{2}\right)=\dfrac{3}{4}$ をとる。

このとき、②より $b=\boldsymbol{\dfrac{3}{2}}$ であり、①より
$$\dfrac{t}{s}=-1+\dfrac{2}{1-\sqrt{1-\dfrac{3}{4}}}=\mathbf{3}$$

解説

⑴は基本事項の組み合わせなので問題ないと思います。

⑵で、①の変形が思いつかず
$$\dfrac{t}{s} = \dfrac{1+\sqrt{1-ab}}{1-\sqrt{1-ab}} = \dfrac{(1+\sqrt{1-ab})^2}{ab}$$としてしまった場合でも、遠回りにはなりますが答えには辿り着けます。

$k=\sqrt{1-ab}$ とおくと、$ab=1-k^2$ となるので
$$\dfrac{t}{s} = \dfrac{(1+k)^2}{1-k^2} = \dfrac{1+k}{1-k} \ \cdots (*)$$と変形できます。$ab$ の範囲は $0\lt ab \leqq \dfrac{3}{4}$ なので、$\dfrac{1}{2}\leqq k \lt 1$ と分かり、あとは $(*)$ 式を次数下げするなり微分するなりして、最小値を求めることができます。

$(*)$ 式で次数下げをするくらいなら初めからやった方が断然ラクですが、$\sqrt{1-ab}$ をまるごと $1$ 文字と見て分子から消去するのは確かに盲点かもしれません。

まとめ

今回は、大阪大学理系数学（2021年 第1問）の解説をしました。