今回は、東京大学理系数学(2021年 第2問)の解説をしたいと思います。
問題
複素数 $a,b,c$ に対して整式 $f(z)=az^2+bz+c$ を考える。$i$ を虚数単位とする。
⑴ $\alpha,\beta,\gamma$ を複素数とする。$f(0)=\alpha, \ f(1)=\beta, \ f(i)=\gamma$ が成り立つとき,$a,b,c$ をそれぞれ $\alpha,\beta,\gamma$ で表せ。
⑵ $f(0),f(1),f(i)$ がいずれも $1$ 以上 $2$ 以下の実数であるとき,$f(2)$ のとりうる範囲を複素数平面上に図示せよ。
(東京大学)
解答
⑴
$f(0)=\alpha, \ f(1)=\beta, \ f(i)=\gamma$ より
$$\left\{
\begin{eqnarray}
c &=& \alpha \\
a+b+c &=& \beta \\
-a+bi+c &=& \gamma
\end{eqnarray}
\right.$$
これを解くと
$$\left\{
\begin{eqnarray}
a &=& \boldsymbol{-i\alpha + \dfrac{1+i}{2}\beta + \dfrac{-1+i}{2}\gamma} \\
b &=& \boldsymbol{(-1+i)\alpha + \dfrac{1-i}{2}\beta + \dfrac{1-i}{2}\gamma} \\
c &=& \boldsymbol{\alpha} \\
\end{eqnarray}
\right.
$$
$$\left\{
\begin{eqnarray}
a &=& \boldsymbol{-i\alpha + \dfrac{1+i}{2}\beta + \dfrac{-1+i}{2}\gamma} \\
b &=& \boldsymbol{(-1+i)\alpha + \dfrac{1-i}{2}\beta + \dfrac{1-i}{2}\gamma} \\
c &=& \boldsymbol{\alpha} \\
\end{eqnarray}
\right.
$$
⑵
⑴より
$$\begin{eqnarray}
f(2) &=& 4a+2b+c \\
&=& 4\left( -i\alpha + \dfrac{1+i}{2}\beta + \dfrac{-1+i}{2}\gamma \right) \\
&&+2\left\{ (-1+i)\alpha + \dfrac{1-i}{2}\beta + \dfrac{1-i}{2}\gamma \right\} \\
&&+ \alpha \\
&=& (-1-2i)\alpha+(3+i)\beta+(-1+i)\gamma
\end{eqnarray}$$ただし、$\alpha,\beta,\gamma$ はいずれも $1$ 以上 $2$ 以下の実数である。
ここで
$$\begin{eqnarray}
z_1 &=& -1-2i, \\
z_2 &=& 3+i, \\
z_3 &=& -1+i
\end{eqnarray}$$とおくと
$$f(2) = \alpha z_1 +\beta z_2 +\gamma z_3$$となる。
$\alpha,\beta$ が $1$ 以上 $2$ 以下を動くとき、$\alpha z_1 +\beta z_2$ は下図の網掛け部分のように平行四辺形の周および内部を動く。この領域を $D$ とおく。
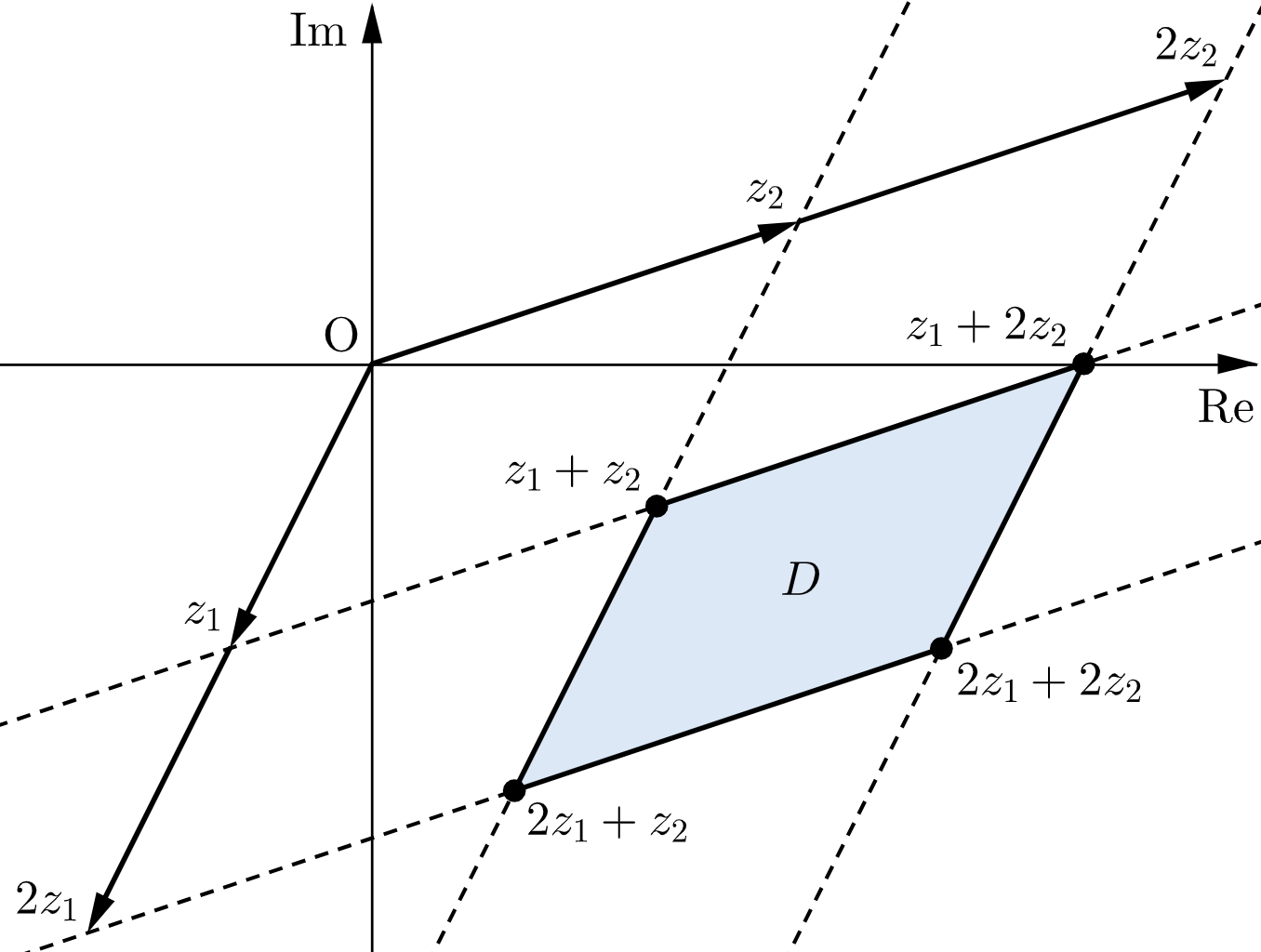
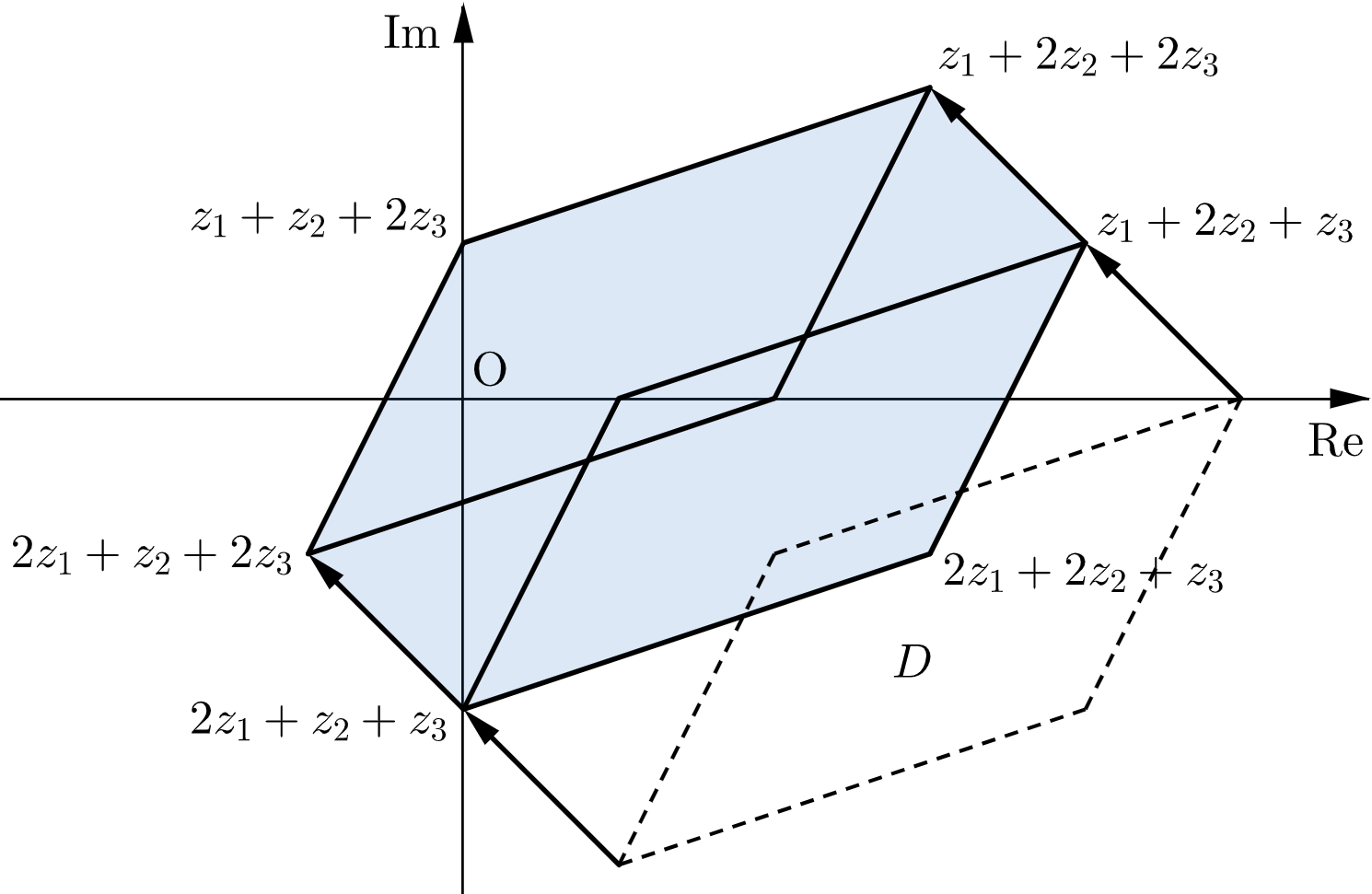
$D$ 内の任意の点に $\gamma z_3$ を足すと、$D$ は $\gamma z_3$ だけ平行移動する。$\gamma$ が$1$ から $2$ まで動くとき、$D$ は「 $D$ を $z_3$ だけ平行移動した位置」から「 $D$ を $2z_3$ だけ平行移動した位置」まで平行移動する。
この通過範囲は下図の網掛け部分のようになり、これが $f(2)$ のとりうる範囲となる。
よって、$f(2)$ のとりうる範囲は
$$\begin{array}{lll}
z_1+z_2+2z_3=i, & z_1+2z_2+2z_3=3+2i, & z_1+2z_2+z_3=4+i, \\
2z_1+2z_2+z_3=3-i, & 2z_1+z_2+z_3=-2i, & 2z_1+z_2+2z_3=-1-i
\end{array}$$の $6$ 点を頂点とする六角形の周および内部、すなわち下図の網掛け部分である。ただし、境界を含む。
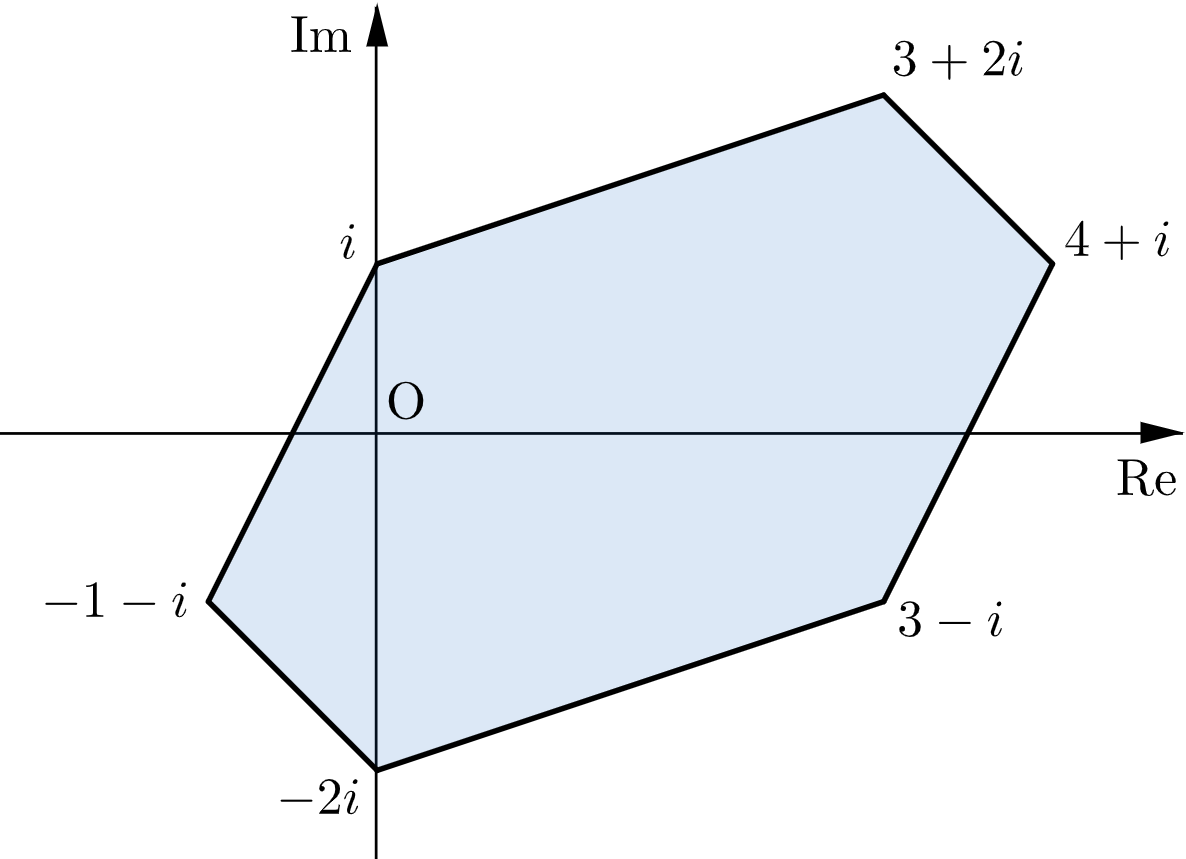
下図の網掛け部分(境界を含む)

解説
⑴は分母の有理化に注意すれば、難しいところはありません。
⑵は複素数平面の問題と言いつつ、ベクトルのように解く問題です。
記述の仕方に迷いますが、図があれば言いたいことは伝わりますので、計算ミスに注意しつつ、最低限の記述と図で答えだけは合わせましょう。
まとめ
今回は、東京大学理系数学(2021年 第2問)の解説をしました。
ほかの問題にもチャレンジしよう!
東京大学 理系数学 2021年 第1問 解説
東京大学 理系数学 2021年 第2問 解説
東京大学 理系数学 2021年 第3問 解説
東京大学 理系数学 2021年 第4問 解説
東京大学 理系数学 2021年 第5問 解説
東京大学 理系数学 2021年 第6問 解説













