京都大学 理系数学 2020年 第1問 解説

今回は、京都大学理系数学（2020年 第1問）の解説をしたいと思います。

問題

　$a,b$ は実数で，$a\gt0$ とする．$z$ に関する方程式
$$z^3+3az^2+bz+1=0\quad(*)$$は $3$ つの相異なる解を持ち，それらは複素数平面上で一辺の長さが $\sqrt{3}a$ の正三角形の頂点となっているとする．このとき，$a,b$ と $(*)$ の $3$ つの解を求めよ．

（京都大学）

解答

$(*)$ の係数はすべて実数なので、その $3$ つの解は「すべて実数」か「 $1$ つの実数解と $1$ 組の共役な複素数」である。

前者の場合、複素数平面上で正三角形をなさないので、$3$ つの解は後者となる。

このとき、$3$ つの解は $k,\alpha,\overline{\alpha}$ と表せる。ただし、$k$ は実数、$\alpha$ は虚数である。

よって、解と係数の関係より
$$\left\{
\begin{alignat}{2}
&k+\alpha+\overline{\alpha}=-3a& &\quad\cdots\text{①} \\[0.2em]
&k\alpha+k\overline{\alpha}+\alpha\overline{\alpha}=b& &\quad\cdots\text{②} \\[0.2em]
&k\alpha\overline{\alpha}=-1& &\quad\cdots\text{③}
\end{alignat}
\right.$$が成り立つ。

条件より、複素数平面上において、$2$ 点 $\alpha,\overline{\alpha}$ の中点と $k$ の距離は $\sqrt{3}a\cdot\dfrac{\sqrt{3}}{2}=\dfrac{3}{2}a$ なので
$$\left|\dfrac{\alpha+\overline{\alpha}}{2}-k\,\right|=\dfrac{3}{2}a$$となる。

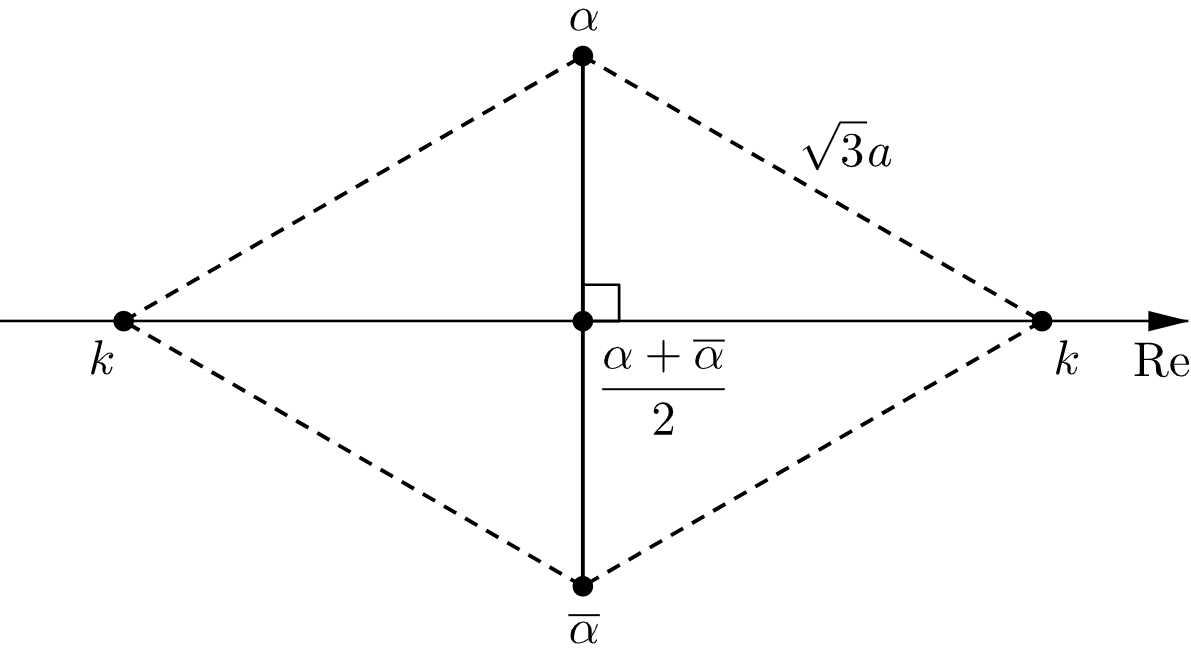
$\dfrac{\alpha+\overline{\alpha}}{2}-k$ は実数なので
$$\begin{align}
\dfrac{\alpha+\overline{\alpha}}{2}-k &= \pm\dfrac{3}{2}a \\[0.3em]
\therefore \ \alpha+\overline{\alpha} &= 2k\pm3a \quad\cdots\text{④}
\end{align}$$

①,④より
$$\begin{align}
k+2k\pm3a &= -3a \\[0.3em]
\therefore \ k &= 0,\,-2a
\end{align}$$

$k=0$ は④に矛盾するので不適。よって
$$k=-2a \quad\cdots\text{⑤}$$

①,⑤より
$$\begin{align}
\alpha+\overline{\alpha} &= -a \quad\cdots\text{⑥} \\[0.3em]
\therefore \ \mathrm{Re}(\alpha) &= -\dfrac{a}{2}
\end{align}$$

また、複素数平面上で $2$ 点 $\alpha,\overline{\alpha}$ は実軸対称であり、条件より両者の距離は $\sqrt{3}a$ なので
$$\mathrm{Im}(\alpha)=\pm\dfrac{\sqrt{3}}{2}a$$

したがって
$$\begin{align}
\alpha &= \dfrac{-1\pm\sqrt{3}i}{2}a \quad\cdots\text{⑦} \\[0.3em]
\alpha\overline{\alpha} &= |\alpha|^2 \\
&= \bigg\{\left(\dfrac{1}{2}\right)^2+\bigg(\pm\dfrac{\sqrt{3}}{2}\bigg)^2\bigg\}a^2 \\
&= a^2 \quad\cdots\text{⑧}
\end{align}$$

③,⑤,⑧より
$$\begin{align}
-2a\cdot a^2 &= -1 \\
\therefore \ a &= \dfrac{1}{\sqrt[ 3 ]{ 2 }} \ \text{（}\because a\gt0 \ \text{）}
\end{align}$$

⑤,⑦より
$$\begin{align}
k &= -\dfrac{2}{\sqrt[ 3 ]{ 2 }}=-\sqrt[ 3 ]{ 4 }\,, \\
\alpha &= \dfrac{-1\pm\sqrt{3}i}{2}\cdot\dfrac{1}{\sqrt[ 3 ]{ 2 }}=\dfrac{\sqrt[ 3 ]{ 4 }(-1\pm\sqrt{3}i)}{4}
\end{align}$$

②,⑤,⑥,⑧より
$$\begin{align}
b &= k(\alpha+\overline{\alpha})+\alpha\overline{\alpha} \\
&= -2a\cdot(-a)+a^2 \\
&= 3a^2 \\
&= \dfrac{3}{\sqrt[ 3 ]{ 4 }}
\end{align}$$

以上より、$a=\boldsymbol{\dfrac{1}{\sqrt[ 3 ]{ 2 }}}$，$b=\boldsymbol{\dfrac{3}{\sqrt[ 3 ]{ 4 }}}$，$(*)$ の解は $z=\boldsymbol{-\sqrt[ 3 ]{ 4 }}\,, \ \boldsymbol{\dfrac{\sqrt[ 3 ]{ 4 }(-1\pm\sqrt{3}i)}{4}}$ である。

解説

$(*)$ が実数係数の方程式なので、ある虚数解をもつとき、その共役な複素数も解になることに気づけるかどうかがポイントです。

また、共役な複素数は実軸対称であることも踏まえて、与えられた条件を式で表して処理していけば、答えにたどり着けると思います。

$\alpha+\overline{\alpha}$ が実数（$\,2\mathrm{Re}(\alpha)\,$）になることは忘れがちなので、覚えておきましょう。

まとめ

今回は、京都大学理系数学（2020年 第1問）の解説をしました。