京都大学 理系数学 2020年 第3問 解説

今回は、京都大学理系数学（2020年 第3問）の解説をしたいと思います。

問題

　$k$ を正の実数とする．座標空間において，原点 $\mathrm{O}$ を中心とする半径 $1$ の球面上の $4$ 点 $\mathrm{A},\,$$\mathrm{B},\,$$\mathrm{C},\,$$\mathrm{D}$ が次の関係式を満たしている．
$$\begin{array}{l}
\overrightarrow{\mathrm{OA}}\cdot\overrightarrow{\mathrm{OB}}=\overrightarrow{\mathrm{OC}}\cdot\overrightarrow{\mathrm{OD}}=\dfrac{1}{2}, \\
\overrightarrow{\mathrm{OA}}\cdot\overrightarrow{\mathrm{OC}}=\overrightarrow{\mathrm{OB}}\cdot\overrightarrow{\mathrm{OC}}=-\dfrac{\sqrt{6}}{4}, \\
\overrightarrow{\mathrm{OA}}\cdot\overrightarrow{\mathrm{OD}}=\overrightarrow{\mathrm{OB}}\cdot\overrightarrow{\mathrm{OD}}=k\,.
\end{array}$$このとき，$k$ の値を求めよ．ただし，座標空間の点 $\mathrm{X},\mathrm{Y}$ に対して，$\overrightarrow{\mathrm{OX}}\cdot\overrightarrow{\mathrm{OY}}$ は $\overrightarrow{\mathrm{OX}}$ と $\overrightarrow{\mathrm{OY}}$ の内積を表す．

（京都大学）

解答

$$\left\{
\begin{alignat}{2}
&\overrightarrow{\mathrm{OA}}\cdot\overrightarrow{\mathrm{OB}}=\overrightarrow{\mathrm{OC}}\cdot\overrightarrow{\mathrm{OD}}=\dfrac{1}{2}& &\quad\cdots\text{①} \\
&\overrightarrow{\mathrm{OA}}\cdot\overrightarrow{\mathrm{OC}}=\overrightarrow{\mathrm{OB}}\cdot\overrightarrow{\mathrm{OC}}=-\dfrac{\sqrt{6}}{4}& &\quad\cdots\text{②} \\
&\overrightarrow{\mathrm{OA}}\cdot\overrightarrow{\mathrm{OD}}=\overrightarrow{\mathrm{OB}}\cdot\overrightarrow{\mathrm{OD}}=k& &\quad\cdots\text{③}
\end{alignat}
\right.$$

$4$ 点 $\mathrm{A},\mathrm{B},\mathrm{C},\mathrm{D}$ は原点 $\mathrm{O}$ を中心とする半径 $1$ の球面上にあるので
$$|\overrightarrow{\mathrm{OA}}|=|\overrightarrow{\mathrm{OB}}|=|\overrightarrow{\mathrm{OC}}|=|\overrightarrow{\mathrm{OD}}|=1$$

①より
$$\begin{align}
|\overrightarrow{\mathrm{OA}}||\overrightarrow{\mathrm{OB}}|\cos\angle\mathrm{AOB} &= \dfrac{1}{2} \\
\cos\angle\mathrm{AOB} &= \dfrac{1}{2} \\
\therefore \ \angle\mathrm{AOB} &= \dfrac{\pi}{3}
\end{align}$$

同様に $\angle\mathrm{COD}=\dfrac{\pi}{3}$ となり、$\triangle\mathrm{AOB}$ と $\triangle\mathrm{AOB}$ はともに $1$ 辺の長さが $1$ の正三角形となる。

$\mathrm{A}\bigg(\dfrac{\sqrt{3}}{2},\,\dfrac{1}{2},\,0\bigg)$，$\mathrm{B}\bigg(\dfrac{\sqrt{3}}{2},\,-\dfrac{1}{2},\,0\bigg)$ としても一般性を失わない。

②より
$$\begin{align}
|\overrightarrow{\mathrm{OA}}||\overrightarrow{\mathrm{OC}}|\cos\angle\mathrm{AOC} &= |\overrightarrow{\mathrm{OB}}||\overrightarrow{\mathrm{OC}}|\cos\angle\mathrm{BOC} \\[0.2em]
\cos\angle\mathrm{AOC} &= \cos\angle\mathrm{BOC} \\[0.2em]
\therefore \ \angle\mathrm{AOC} &= \angle\mathrm{BOC}
\end{align}$$となるから、点 $\mathrm{C}$ は $xz$ 平面上、とくに円 $x^2+z^2=1$ の上に存在する。

同様に③から、点 $\mathrm{D}$ も円 $x^2+z^2=1$ の上に存在する。

よって、$0\leqq\alpha\lt2\pi$，$0\leqq\beta\lt2\pi$ を満たす実数を用いて
$$\mathrm{C}(\cos\alpha,\,0,\,\sin\alpha),\quad\mathrm{D}(\cos\beta,\,0,\,\sin\beta)$$とおける。

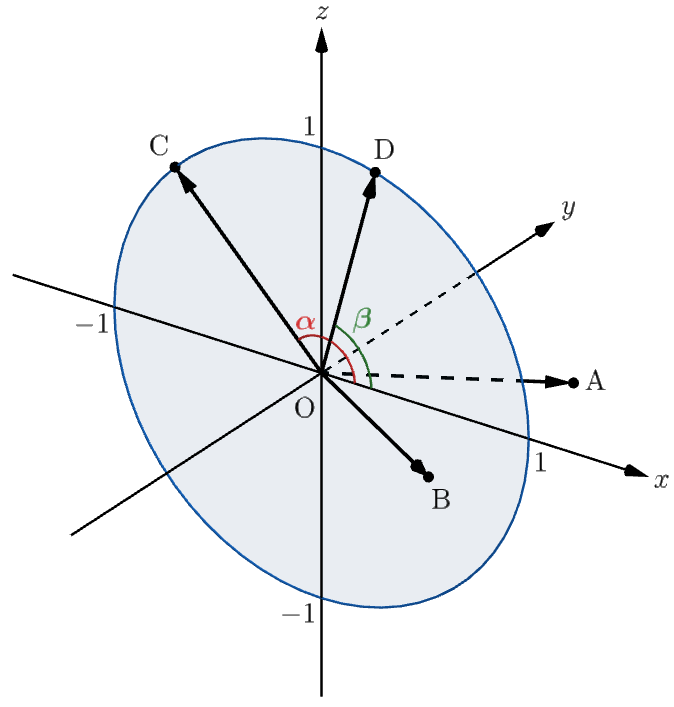
②より
$$\begin{align}
-\dfrac{\sqrt{6}}{4} &= \overrightarrow{\mathrm{OA}}\cdot\overrightarrow{\mathrm{OC}} \ (=\overrightarrow{\mathrm{OB}}\cdot\overrightarrow{\mathrm{OC}}) \\
&= \dfrac{\sqrt{3}}{2}\cos\alpha \\
\cos\alpha &= -\dfrac{\sqrt{2}}{2} \\
\therefore \ \alpha &= \dfrac{3}{4}\pi
\end{align}$$

$\angle\mathrm{COD}=\dfrac{\pi}{3}$ より
$$\beta=\alpha\pm\dfrac{\pi}{3}=\dfrac{13}{12}\pi,\,\dfrac{5}{12}\pi$$となる。

$\beta=\dfrac{13}{12}\pi$ のとき、$\dfrac{\pi}{2}\lt\beta\lt\dfrac{3}{2}\pi$ より
$$\overrightarrow{\mathrm{OA}}\cdot\overrightarrow{\mathrm{OD}}=\dfrac{\sqrt{3}}{2}\cos\dfrac{13}{12}\pi\lt0$$となり、$k\gt0$ に矛盾するので不適。

$\beta=\dfrac{5}{12}\pi$ のとき、$0\lt\beta\lt\dfrac{\pi}{2}$ より
$$\overrightarrow{\mathrm{OA}}\cdot\overrightarrow{\mathrm{OD}}=\dfrac{\sqrt{3}}{2}\cos\dfrac{5}{12}\pi\gt0$$となり、$k\gt0$ に適する。

したがって
$$\begin{align}
k &= \dfrac{\sqrt{3}}{2}\cos\dfrac{5}{12}\pi \\
&= \dfrac{\sqrt{3}}{2}\cos\left(\dfrac{3}{4}\pi-\dfrac{\pi}{3}\right) \\
&= \dfrac{\sqrt{3}}{2}\cdot\bigg(-\dfrac{\sqrt{2}}{2}\cdot\dfrac{1}{2}+\dfrac{\sqrt{2}}{2}\cdot\dfrac{\sqrt{3}}{2}\bigg) \\
&= \boldsymbol{\dfrac{3\sqrt{2}-\sqrt{6}}{8}}
\end{align}$$

解説

対称性が多く、どこの角度が等しいのか図を描いてイメージしましょう。

点 $\mathrm{C},\mathrm{D}$ が $2$ 点 $\mathrm{A},\mathrm{B}$ から等距離にある平面（解答でいえば $xz$ 平面）上にあると分かれば、点 $\mathrm{C}$ の位置を求めることで自動的に $\mathrm{D}$ の位置も決まります。

なお、点 $\mathrm{D}$ の位置は $2$ 通り考えられますが、$k\gt0$ に注意して $1$ つに絞りましょう。

まとめ

今回は、京都大学理系数学（2020年 第3問）の解説をしました。