大阪大学 理系数学 2022年 第5問 解説

今回は、大阪大学理系数学（2022年 第5問）の解説をしたいと思います。

問題

　座標平面において，$t$ を媒介変数として
$$x=e^t\cos t+e^{\pi}, \quad y=e^t\sin t \quad(0\leqq t\leqq \pi)$$で表される曲線を $C$ とする．曲線 $C$ と $x$ 軸で囲まれた部分の面積を求めよ．

（大阪大学）

解答

解法1

$x(t)=e^t\cos t+e^{\pi}, \quad y(t)=e^t\sin t$ とおくと
$$\begin{eqnarray}
\dfrac{dx}{dt}&=&e^t\cos t+e^t(-\sin t)=\sqrt{2}e^t\cos\left(t+\dfrac{\pi}{4}\right) \\
\dfrac{dy}{dt}&=&e^t\sin t+e^t\cos t=\sqrt{2}e^t\sin\left(t+\dfrac{\pi}{4}\right)
\end{eqnarray}$$

$0\leqq t\leqq \pi$ において
$$\begin{eqnarray}
\dfrac{dx}{dt}=0 \quad &\Longleftrightarrow& \quad t=\dfrac{\pi}{4} \\
\dfrac{dy}{dt}=0 \quad &\Longleftrightarrow& \quad t=\dfrac{3}{4}\pi
\end{eqnarray}$$であるから、$(x,y)$ の増減表は次のようになる。

$$\begin{array}{c|c|c|c|c|c|c|c}\hline
t & 0 & \cdots & \dfrac{\pi}{4} & \cdots & \dfrac{3}{4} & \cdots & \pi \\
\hline
\dfrac{dx}{dt} & & + & 0 & – & – & – & \\
\hline
\dfrac{dy}{dt} & & + & + & + & 0 & – & \\
\hline
x & e^{\pi}+1 & \nearrow & \text{極大} & \searrow & & \searrow & 0 \\
\hline
y & 0 & \nearrow & & \nearrow & \text{極大} & \searrow & 0 \\
\hline
\end{array}$$

よって、曲線 $C$ の概形は下図のようになる。

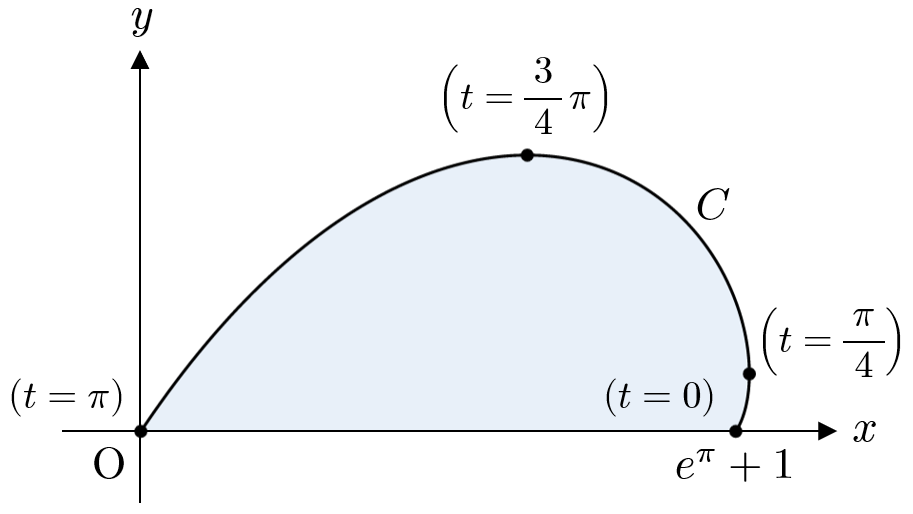
$$\begin{cases}
y_1=y(t) & \left(0\leqq t\leqq \dfrac{\pi}{4}\right) \\
y_2=y(t) & \left(\dfrac{\pi}{4}\leqq t\leqq \pi\right)
\end{cases}$$とおき、求める面積を $S$ とすると
$$\begin{eqnarray}
S &=& \displaystyle \int_{x(\pi)}^{x(\frac{\pi}{4})}y_2dx \ – \displaystyle \int_{x(0)}^{x(\frac{\pi}{4})}y_1dx \\
&=& \displaystyle \int_{\pi}^{\frac{\pi}{4}}y\dfrac{dx}{dt}dt \ – \displaystyle \int_{0}^{\frac{\pi}{4}}y\dfrac{dx}{dt}dt \\
&=& \displaystyle \int_{\pi}^{0}y\dfrac{dx}{dt}dt \\
&=& \displaystyle \int_{\pi}^{0}e^{2t}\sin t(\cos t-\sin t)dt \\
&=& \displaystyle \int_{\pi}^{0}e^{2t}\left(\dfrac{1}{2}\sin 2t-\dfrac{1-\cos 2t}{2}\right)dt \\[0.5em]
2S &=& \displaystyle \int_{\pi}^{0}e^{2t}(\sin 2t+\cos 2t)dt \ – \displaystyle \int_{\pi}^{0}e^{2t}dt
\end{eqnarray}$$$\left(\dfrac{1}{2}e^{2t}\sin 2t\right)’=e^{2t}(\sin 2t+\cos 2t)$ より
$$\begin{eqnarray}
2S &=& \left[\dfrac{1}{2}e^{2t}\sin 2t\right]_{\pi}^0-\left[\dfrac{1}{2}e^{2t}\right]_{\pi}^0 \\
&=& \dfrac{1}{2}(e^{2\pi}-1)
\end{eqnarray}$$

よって、求める面積は
$$S=\boldsymbol{\dfrac{1}{4}\left(e^{2\pi}-1\right)}$$

解法2

曲線 $C$ を $x$ 軸方向に $-e^{\pi}$ だけ平行移動することで得られる、
$$x=e^t\cos t, \quad y=e^t\sin t \quad(0\leqq t\leqq \pi)$$ で表される曲線を $C’$ とすると、求める面積は、曲線 $C’$ と $x$ 軸で囲まれた部分の面積 $S$ に等しい。

曲線 $C’$ を極方程式で表すと $r=e^t$ であるから、求める面積は
$$\begin{eqnarray}
S &=& \displaystyle \int_{0}^{\pi}\dfrac{1}{2}r^2dt=\displaystyle \int_{0}^{\pi}\dfrac{1}{2}e^{2t}dt \\[0.5em]
&=& \left[\dfrac{1}{4}e^{2t}\right]_{0}^{\pi}=\boldsymbol{\dfrac{1}{4}\left(e^{2\pi}-1\right)}
\end{eqnarray}$$

解説

「解法1」は練習問題などでも経験があるであろうスタンダードな解き方です。計算ミスに注意して丁寧に解きましょう。

$S$ を求める際、いきなり $\displaystyle \int_{\pi}^{0}y\dfrac{dx}{dt}dt$ としてはいけません。区間を分割した結果そうなった、という「過程」をちゃんと書きましょう。

また、途中式にでてきた $\left(\dfrac{1}{2}e^{2t}\sin 2t\right)’=e^{2t}(\sin 2t+\cos 2t)$ が思いつかない場合、部分積分を繰り返し使うことでも積分を計算することができ、以下に示します：

「解法2」は極方程式を使った鮮やかな解法ですが、極座標表示された曲線で囲まれる面積の公式はそこまでメジャーではないので、地道に「解法1」の方法で解く方がかえって確実かもしれません。

まとめ

今回は、大阪大学理系数学（2022年 第5問）の解説をしました。