今回は、東京大学物理(2022年 第1問)の解説をしたいと思います。
前文
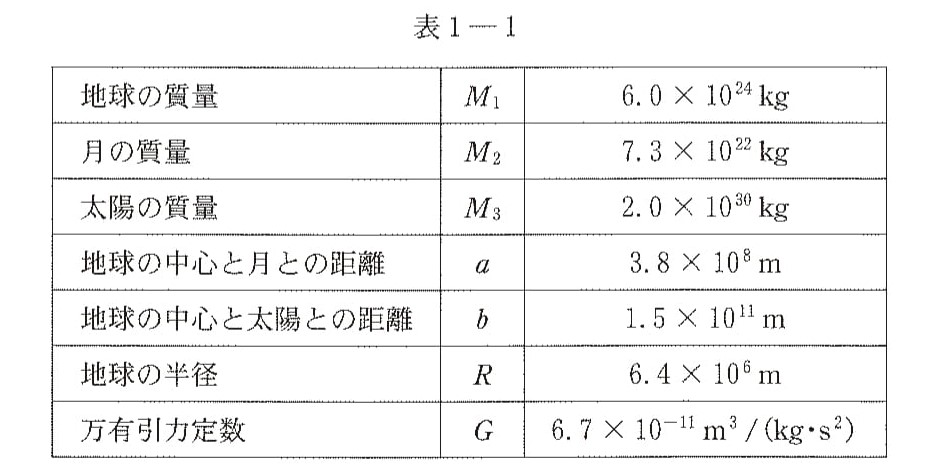
地球表面上の海水は,地球からの万有引力の他に,月や太陽からの引力,さらに地球や月の運動によって引き起こされる様々な力を受ける。これらの力の一部が時間とともに変化することで,潮の満ち干が起こる(潮汐運動)。ここでは,地球の表面に置かれた物体に働く力について,単純化したモデルで考察しよう。なお,万有引力定数を $G$ とし,地球は質量 $M_1$ で密度が一様な半径 $R$ の球体とみなせるとする。以下の設問Ⅰ,Ⅱ,Ⅲに答えよ。
(東京大学)
Ⅰ
問題
地球の表面に置かれた物体は地球の自転による遠心力を受ける。地球の自転周期を $T_1$ とするとき,以下の設問に答えよ。
⑴ 質量 $m$ の質点が赤道上のある地点 $\mathrm{E}$ に置かれたときに働く遠心力の大きさ $f_0$,および北緯 $45^{\circ}$ のある地点 $\mathrm{F}$ に置かれたときに働く遠心力の大きさ $f_1$ を求め,それぞれ $m$,$R$,$T_1$ を用いて表せ。
⑵ 設問Ⅰ⑴の地点 $\mathrm{E}$ における,地球の自転による遠心力の効果を含めた重力加速度 $g_0$ を求め,$G$,$M_1$,$R$,$T_1$ を用いて表せ。
(東京大学)
解答
⑴
地球の自転角速度を $\omega_0$ とすると、$\omega_0=\dfrac{2\pi}{T_1}$ より
$$f_0=mR\omega_0^2=mR\left(\dfrac{2\pi}{T_1}\right)^2=\style{border-bottom:double 4px;padding-bottom:3px}{\boldsymbol{\dfrac{4\pi^2mR}{T_1^2}}}$$
地点 $\mathrm{F}$ では回転半径が $R\cos 45^{\circ}=\dfrac{R}{\sqrt{2}}$ となるので
$$f_1=m\dfrac{R}{\sqrt{2}}\omega_0^2=m\dfrac{R}{\sqrt{2}}\left(\dfrac{2\pi}{T_1}\right)^2=\style{border-bottom:double 4px;padding-bottom:3px}{\boldsymbol{\dfrac{2\sqrt{2}\pi^2mR}{T_1^2}}}$$
⑵
万有引力と遠心力との合力が重力であるから
$$\begin{eqnarray}
mg_0 &=& G\dfrac{mM_1}{R^2}-f_0=G\dfrac{mM_1}{R^2}-\dfrac{4\pi^2mR}{T_1^2} \\
\therefore \quad g_0 &=& \style{border-bottom:double 4px;padding-bottom:3px}{\boldsymbol{\dfrac{GM_1}{R^2}-\dfrac{4\pi^2R}{T_1^2}}}
\end{eqnarray}$$
Ⅱ
問題
次に,月からの引力と,月が地球の周りを公転運動することによって発生する力を考える。ここではこれらの力についてのみ考えるため,地球が自転しないという仮想的な場合について考察する。
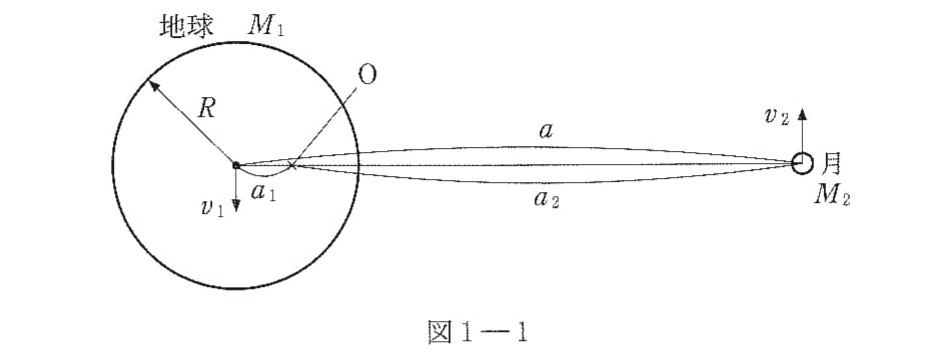
月が地球の周りを公転するとき,地球と月は,地球と月の重心である点 $\mathrm{O}$ を中心に同一周期で円運動をすると仮定する(図 $1$ ― $1$ )。なお,図 $1$ ― $1$ において,この円運動の回転軸は紙面に垂直である。月は質量 $M_2$ の質点とし,地球の中心と月との距離を $a$ とする。また,地球の中心および月から点 $\mathrm{O}$ までの距離をそれぞれ $a_1$,$a_2$ とする。以下の設問に答えよ。⑴ 点 $\mathrm{O}$ から見た地球の中心および月の速さをそれぞれ $v_1$,$v_2$ とする。$v_1$ および $v_2$ を $a$,$G$,$M_1$,$M_2$ を用いて表せ。
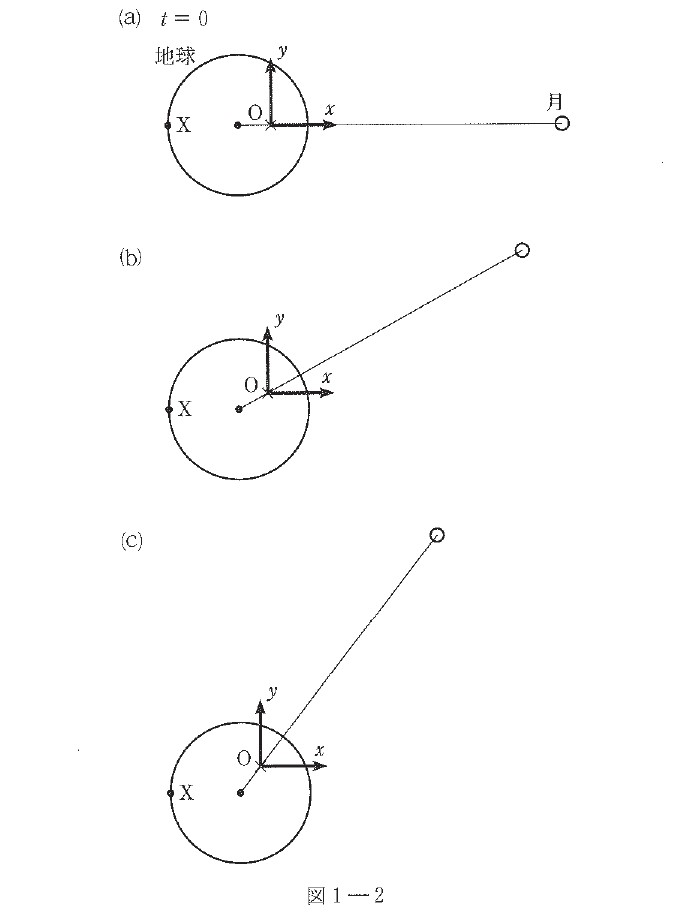
⑵ 点 $\mathrm{O}$ を原点として固定した $xy$ 座標系を,図 $1$ ― $2$ ⒜のように紙面と同一平面にとる。時刻 $t=0$ において,座標が $(-a_1-R, \ 0)$ である地球表面上の点を点 $\mathrm{X}$ とする。月の公転周期を $T_2$ とするとき,時刻 $t$ における点 $\mathrm{X}$ の座標を $a_1$,$R$,$T_2$,$t$ を用いて表せ。ただし,地球の自転を無視しているため,時刻 $t=0$ 以降で図 $1$ ― $2$ ⒝,⒞のように位置関係が変化することに注意せよ。
⑶ 設問Ⅱ⑵の点 $\mathrm{X}$ に,$M_1$ および $M_2$ に比して十分に小さい質量 $m$ の質点が置かれているときを考える。この質点について,地球が点 $\mathrm{O}$ を中心とした円運動をすることで生じる遠心力の大きさ $f_c$ を求め,$G$,$m$,$M_2$,$a$ を用いて表せ。
⑷ ある時刻において,地球表面上で月から最も遠い点を $\mathrm{P}$,月に最も近い点を $\mathrm{Q}$ とする。質量 $m$ の質点を点 $\mathrm{P}$ および点 $\mathrm{Q}$ に置いた場合に,質点に働く遠心力と月からの万有引力の合力の大きさをそれぞれ $f_{\mathrm{P}}$,$f_{\mathrm{Q}}$ とする。$f_{\mathrm{P}}$,$f_{\mathrm{Q}}$ を $G$,$m$,$M_2$,$a$,$R$ を用いて表せ。また,点 $\mathrm{P}$ および点 $\mathrm{Q}$ における合力の向きは月から遠ざかる方向か,近づく方向かをそれぞれ答えよ。
(東京大学)
解答
⑴
点 $\mathrm{O}$ は地球と月の重心なので
$$a_1=\dfrac{M_2}{M_1+M_2}a, \quad a_2=\dfrac{M_1}{M_1+M_2}a$$
地球についての運動方程式より
$$\begin{eqnarray}
M_1\dfrac{v_1^2}{a_1} &=& G\dfrac{M_1M_2}{a^2} \\
\therefore \quad v_1 &=& \sqrt{\dfrac{GM_2}{a^2}\cdot\dfrac{M_2}{M_1+M_2}a} \\
&=& \style{border-bottom:double 4px;padding-bottom:3px}{\boldsymbol{\sqrt{\dfrac{G}{(M_1+M_2)a}}M_2}}
\end{eqnarray}$$
同様に、月についての運動方程式より
$$\begin{eqnarray}
M_2\dfrac{v_2^2}{a_2} &=& G\dfrac{M_1M_2}{a^2} \\
\therefore \quad v_2 &=& \sqrt{\dfrac{GM_2}{a^2}\cdot\dfrac{M_1}{M_1+M_2}a} \\
&=& \style{border-bottom:double 4px;padding-bottom:3px}{\boldsymbol{\sqrt{\dfrac{G}{(M_1+M_2)a}}M_1}}
\end{eqnarray}$$
⑵
点 $\mathrm{O}$ を中心とした地球の円運動の周期は月の公転周期と等しく $T_2$ であるから、角速度を $\omega_1$ とすると $\omega_1=\dfrac{2\pi}{T_2}$ となる。
よって、地球の中心の点を $\mathrm{C}$ とすると、点 $\mathrm{C}$ の座標は $\left( a_1\cos \left( \omega_1t+\pi \right), \ a_1\sin \left( \omega_1t+\pi \right) \right)$ すなわち $\left( -a_1\cos \left( \dfrac{2\pi}{T_2}t \right), \ -a_1\sin \left( \dfrac{2\pi}{T_2}t \right) \right)$ と表される。
点 $\mathrm{X}$ は常に点 $\mathrm{C}$ を $x$ 軸方向に $-R$ だけ平行移動した点に位置するので、求める座標は
$$\style{border-bottom:double 4px;padding-bottom:3px}{\boldsymbol{\left( -a_1\cos \left( \dfrac{2\pi}{T_2}t \right)-R, \ -a_1\sin \left( \dfrac{2\pi}{T_2}t \right) \right)}}$$
⑶
⑴,⑵より、点 $\mathrm{X}$ は 半径 $a_1$ の円周上を速さ $v_1$ で円運動するので、
$$\begin{eqnarray}
f_c &=& m\dfrac{v_1^2}{a_1} = m\cdot \dfrac{GM_2^2}{(M_1+M_2)a}\cdot \dfrac{M_1+M_2}{M_2a} \\
&=& \style{border-bottom:double 4px;padding-bottom:3px}{\boldsymbol{G\dfrac{M_2m}{a^2}}}
\end{eqnarray}$$
⑷
質量 $m$ の質点を点 $\mathrm{P}$ に置いたときの、質点に働く遠心力および月からの万有引力の大きさをそれぞれ $f_{\mathrm{P}1}$、$f_{\mathrm{P}2}$ とし、点 $\mathrm{Q}$ に置いたときも同様にそれぞれ $f_{\mathrm{Q}1}$、$f_{\mathrm{Q}2}$ とする。
地球上のすべての点は、点 $\mathrm{X}$ と同じく半径 $a_1$ の円周上を速さ $v_1$ で円運動するので、⑶より
$$f_{\mathrm{P}1}=f_{\mathrm{Q}1}=f_c=G\dfrac{M_2m}{a^2}$$
点 $\mathrm{P}$ および 点 $\mathrm{Q}$ から月までの距離はそれぞれ $a+R$,$a-R$ であるから、
$$f_{\mathrm{P}2}=G\dfrac{M_2m}{(a+R)^2}, \quad f_{\mathrm{Q}2}=G\dfrac{M_2m}{(a-R)^2}$$
よって、月から遠ざかる方向を正とする合力は
$$\begin{eqnarray}
\text{点} \ \mathrm{P}\text{:}f_{\mathrm{P}1}-f_{\mathrm{P}2} &=& G\dfrac{M_2m}{a^2}-G\dfrac{M_2m}{(a+R)^2} \\
&=& GM_2m\left\{ \dfrac{1}{a^2}-\dfrac{1}{(a+R)^2} \right\}\gt 0 \\[0.5em]
\text{点} \ \mathrm{Q}\text{:}f_{\mathrm{Q}1}-f_{\mathrm{Q}2} &=& G\dfrac{M_2m}{a^2}-G\dfrac{M_2m}{(a-R)^2} \\
&=& GM_2m\left\{ \dfrac{1}{a^2}-\dfrac{1}{(a-R)^2} \right\}\lt 0
\end{eqnarray}$$
したがって、求める合力の大きさと向きは
$$\begin{align}
\text{点} \ \mathrm{P} \text{:}&\text{大きさは} \ \style{border-bottom:double 4px;padding-bottom:3px}{\boldsymbol{f_{\mathrm{P}}=GM_2m\left\{ \dfrac{1}{a^2}-\dfrac{1}{(a+R)^2} \right\}}}\text{、} \\
&\text{向きは}\style{border-bottom:double 4px;padding-bottom:3px}{\mathbf{\text{月から遠ざかる方向}}} \\[0.5em]
\text{点} \ \mathrm{Q} \text{:}&\text{大きさは} \ \style{border-bottom:double 4px;padding-bottom:3px}{\boldsymbol{f_{\mathrm{Q}}=GM_2m\left\{ \dfrac{1}{(a-R)^2}-\dfrac{1}{a^2} \right\}}}\text{、} \\
&\text{向きは}\style{border-bottom:double 4px;padding-bottom:3px}{\mathbf{\text{月に近づく方向}}}
\end{align}$$
Ⅲ
問題
さらに,太陽からの引力と,地球の公転運動によって発生する力について考える。これらの力についても設問Ⅱと同様に考えられるものとする。なお,地球と太陽の重心を点 $\mathrm{O}’$ とする。太陽は質量 $M_3$ の質点とし,地球の中心と太陽の距離を $b$ とする。
図 $1$ ― $3$ のように,ある時刻において地球表面上で太陽から最も遠い点を $\mathrm{S}$ とする。質量 $m$ の質点が点 $\mathrm{S}$ に置かれたとき,地球が点 $\mathrm{O}’$ を中心とした円運動をすることで生じる遠心力と太陽からの万有引力の合力の大きさを $f_{\mathrm{S}}$ とする。設問Ⅱ⑷で求めた $f_{\mathrm{P}}$ に対する $f_{\mathrm{S}}$ の比は以下のように見積もることができる。
$$0. \ \bbox[3px,border: 2px solid]{\text{ア}} \lt \dfrac{f_{\mathrm{S}}}{f_{\mathrm{P}}} \lt 0. \ \bbox[3px,border: 2px solid]{\text{イ}}$$$\bbox[3px,border: 2px solid]{\text{ア}}$ と $\bbox[3px,border: 2px solid]{\text{イ}}$ には連続する $1$ 桁の数字が入る。表 $1$ ― $1$ の中から必要な数値を用いて計算し,$\bbox[3px,border: 2px solid]{\text{ア}}$ に入る数字を答えよ。(東京大学)
解答
設問Ⅱより
$$f_{\mathrm{S}}=GM_3m\left\{ \dfrac{1}{b^2}-\dfrac{1}{(b+R)^2} \right\}$$
ここで、$a\gg R$ なので
$$\begin{eqnarray}
f_{\mathrm{P}}&=&GM_2m\left\{ \dfrac{1}{a^2}-\dfrac{1}{(a+R)^2} \right\} \\[0.5em]
&=&GM_2m\dfrac{2aR+R^2}{a^2(a+R)^2}\fallingdotseq GM_2m\dfrac{2aR}{a^2\cdot a^2} \\[0.5em]
&=&\dfrac{2GM_2mR}{a^3}
\end{eqnarray}$$と近似できる。
同様に、$b\gg R$ なので
$$f_{\mathrm{S}}\fallingdotseq \dfrac{2GM_3mR}{b^3}$$と近似できる。
よって、
$$\begin{eqnarray}
\dfrac{f_{\mathrm{S}}}{f_{\mathrm{P}}}&\fallingdotseq& \dfrac{2GM_3mR}{b^3}\cdot\dfrac{a^3}{2GM_2mR}=\dfrac{M_3}{M_2}\left(\dfrac{a}{b}\right)^3 \\[0.5em]
&=&\dfrac{2.0\times 10^{30}}{7.3\times 10^{22}}\cdot\left(\dfrac{3.8\times 10^8}{1.5\times 10^{11}}\right)^3=0.44\cdots
\end{eqnarray}$$
したがって、$\bbox[3px,border: 2px solid]{\text{ア}}$ に入る数字は $\style{border-bottom:double 4px;padding-bottom:3px}{\boldsymbol{4}}$ である。
答え一覧
Ⅰ
$$\begin{align}
\text{⑴}\quad & f_0=\dfrac{4\pi^2mR}{T_1^2} \\[0.5em]
& f_1=\dfrac{2\sqrt{2}\pi^2mR}{T_1^2} \\[0.5em]
\text{⑵}\quad & \dfrac{GM_1}{R^2}-\dfrac{4\pi^2R}{T_1^2}
\end{align}$$
Ⅱ
$$\begin{align}
\text{⑴}\quad & v_1=\sqrt{\dfrac{G}{(M_1+M_2)a}}M_2 \\[0.5em]
& v_2=\sqrt{\dfrac{G}{(M_1+M_2)a}}M_1 \\[0.5em]
\text{⑵}\quad & \left( -a_1\cos \left( \dfrac{2\pi}{T_2}t \right)-R, \ -a_1\sin \left( \dfrac{2\pi}{T_2}t \right) \right) \\[0.5em]
\text{⑶}\quad & G\dfrac{M_2m}{a^2} \\[0.5em]
\text{⑷}\quad & \text{点} \ \mathrm{P} \text{:}f_{\mathrm{P}}=GM_2m\left\{ \dfrac{1}{a^2}-\dfrac{1}{(a+R)^2} \right\}\text{、月から遠ざかる方向} \\[0.5em]
& \text{点} \ \mathrm{Q} \text{:}f_{\mathrm{Q}}=GM_2m\left\{ \dfrac{1}{(a-R)^2}-\dfrac{1}{a^2} \right\}\text{、月に近づく方向}
\end{align}$$
Ⅲ$\quad 4$
まとめ
今回は、東京大学物理(2022年 第1問)の解説をしました。