京都大学 物理 2021年 問題Ⅰ 解説

今回は、京都大学物理（2021年 問題Ⅰ）の解説をしたいと思います。

前文

　次の文章を読んで，$\bbox[3px,border: 2px solid]{~~~~\color{ #efefef }{\text{｜}}~~~~}$ に適した式または数値を，それぞれの解答欄に記入せよ。なお，$\bbox[1px,border: 4px double]{~~~~\color{ #efefef }{\text{｜}}~~~~}$ はすでに $\bbox[3px,border: 2px solid]{~~~~\color{ #efefef }{\text{｜}}~~~~}$ で与えられたものと同じものを表す。また，問１では，指示にしたがって，解答をそれぞれの解答欄に記入せよ。ただし，重力加速度の大きさは $g$ とする。

（京都大学）

⑴

問題

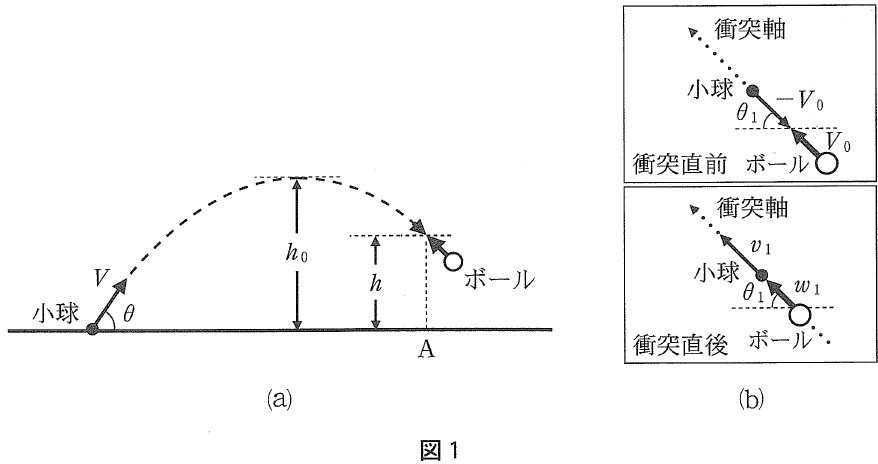
　図1⒜のように，質量 $m$ の小球を，初速度の大きさ $V$，地表から上向きに角度 $\theta$ で投げ上げる。小球は最大高度 $h_0$ に達した後，落下し始めるが，地点 $\mathrm{A}$ の高度 $h$ において，質量 $M$ のボールと一次元的に衝突させ，その反動を利用して小球を高く跳ね上げる。ここで一次元的に衝突するとは，図1⒝のように衝突直前直後の小球とボールが同一直線上に沿って運動することをさし，その直線に沿う衝突軸を定義する。衝突軸は衝突直前のボールの進行方向を正とし，衝突軸方向の速度成分を，以下略して「速度成分」と記載する。なお，衝突は瞬間的に起こるものとし，小球とボールの大きさ，および空気抵抗の影響は無視する。

　図1⒝のように，衝突直前の小球について，その速度の大きさを $V_0$，速度の方向と水平面とのなす角の大きさを $\theta_1$ とすると，$V$，$\theta$，$h$，$g$ を用いて $V_0=\bbox[3px,border: 2px solid]{~~~~\mathbf{\text{ア}}~~~~}$，$\sin\theta_1=\bbox[3px,border: 2px solid]{~~~~\mathbf{\text{イ}}~~~~}$ と表せる。衝突直後の小球，ボールの速度成分をそれぞれ $v_1$，$w_1$ と表し，衝突直前のボールの速度の大きさが小球と同様に $V_0$ だったとすると，運動量保存則は次式で表される。
$$mv_1+Mw_1=\bbox[3px,border: 2px solid]{~~~~\mathbf{\text{ウ}}~~~~}\tag{ⅰ}$$ここで、$\bbox[2px,border: 4px double]{~~~~\mathbf{\text{ウ}}~~~~}$ は $m$，$M$，および $V_0$ を用いて表される量である。衝突が弾性衝突であったとすると，
$$1=-\dfrac{v_1-w_1}{\bbox[3px,border: 2px solid]{~~~~\mathbf{\text{エ}}~~~~}}\tag{ⅱ}$$が成り立つので，式 $(\text{ⅰ})$，$(\text{ⅱ})$ より，衝突直後の速度成分 $v_1$，$w_1$ は，$V_0$，$m$，$M$ を用いて $v_1=\bbox[3px,border: 2px solid]{~~~~\mathbf{\text{オ}}~~~~}$，$w_1=\bbox[3px,border: 2px solid]{~~~~\mathbf{\text{カ}}~~~~}$ と表せる。これより，ボールの質量 $M$ が小球の質量 $m$ の $\bbox[3px,border: 2px solid]{~~~~\mathbf{\text{キ}}~~~~}$ 倍だった場合，衝突直後のボールの速度成分 $w_1$ は $0$ となり，衝突直後の小球の速度成分 $v_1$ の大きさは $V_0$ の $\bbox[3px,border: 2px solid]{~~~~\mathbf{\text{ク}}~~~~}$ 倍となる。このとき，跳ね上がった小球が到達する最大高度 $h_1$ は，$h$，$V$，$\theta$，$g$ を用いて $h_1=\bbox[3px,border: 2px solid]{~~~~\mathbf{\text{ケ}}~~~~}$ となる。

（京都大学）

解答

小球についての「投げ上げた直後」と「衝突直前」における力学的エネルギー保存則より
$$\begin{eqnarray}
\dfrac{1}{2}mV^2&=&\dfrac{1}{2}mV_0^2+mgh \\
V_0&=&\bbox[6px,border: 2px solid]{\sqrt{ V^2-2gh }}_\mathbf{\text{ ア}}\quad\cdots\text{①}\\
\end{eqnarray}$$

衝突するまでの小球の運動において、水平方向については速さ $V\cos\theta$ の等速運動であるから、
$V\cos\theta = V_0\cos\theta_1$ より $\cos\theta_1=\dfrac{V\cos\theta}{V_0}$

よって
$$\begin{eqnarray}
\sin\theta_1 &=& \sqrt{ 1-\cos^2\theta_1 } \\
&=& \sqrt{ 1-\dfrac{(V\cos\theta)^2}{V_0^2} } \\
&=& \sqrt{ 1-\dfrac{(V\cos\theta)^2}{V^2-2gh} } \quad(\because\text{①})\\
&=& \sqrt{\dfrac{V^2\left(1-\cos^2\theta\right)-2gh}{V^2-2gh}} \\
&=& \bbox[6px,border: 2px solid]{\sqrt{\dfrac{(V\sin\theta)^2-2gh}{V^2-2gh}}}_\mathbf{\text{ イ}} \quad\cdots\text{②}
\end{eqnarray}$$

衝突直前、小球とボールの速度成分はそれぞれ $-V_0$、$V_0$ であるから、衝突直前直後における運動量保存則より
$$mv_1+Mw_1=\bbox[6px,border: 2px solid]{-mV_0+MV_0}_\mathbf{\text{ ウ}}\tag{ⅰ}$$

さらに、衝突が弾性衝突であったとき、反発係数の式より
$$1=-\dfrac{v_1-w_1}{-V_0-V_0}=-\dfrac{v_1-w_1}{\bbox[6px,border: 2px solid]{-2V_0}_\mathbf{\text{ エ}}}\tag{ⅱ}$$

式 $(\text{ⅰ})$,$(\text{ⅱ})$ を解くと
$$\begin{eqnarray}
v_1&=&\bbox[6px,border: 2px solid]{\dfrac{3M-m}{m+M}V_0}_\mathbf{\text{ オ}}\quad\cdots\text{③} \\
w_1&=&\bbox[6px,border: 2px solid]{\dfrac{M-3m}{m+M}V_0}_\mathbf{\text{ カ}}\quad\cdots\text{④}
\end{eqnarray}$$

衝突直後のボールの速度成分 $w_1$ が $0$ となるとき、④より
$$\dfrac{M-3m}{m+M}V_0=0 \ \Longleftrightarrow \ M=3m\quad\cdots\text{⑤}$$となるから、$M$ は $m$ の $\bbox[6px,border: 2px solid]{3}_\mathbf{\text{ キ}}$ 倍である。

③に⑤を代入すると
$$v_1=\dfrac{3\cdot 3m-m}{m+3m}V_0=2V_0\quad\cdots\text{⑥}$$となるから、$v_1$ は $V_0$ の $\bbox[6px,border: 2px solid]{2}_\mathbf{\text{ ク}}$ 倍である。

衝突後の小球の運動において、水平方向については速さ $v_1\cos\theta_1$ の等速運動であり、最大高度 $h_1$ において速度の鉛直成分は $0$ であるから、小球についての「衝突直後」と「最大高度 $h_1$ 」における力学的エネルギー保存則より

$$\begin{array}{l}
\dfrac{1}{2}mv_1^2+mgh=\dfrac{1}{2}m(v_1\cos\theta_1)^2+mgh_1 \\
\begin{eqnarray}
h_1&=&\dfrac{v_1^2}{2g}\left(1-\cos^2\theta_1\right)+h \\
&=&\dfrac{(2V_0)^2}{2g}\sin^2\theta_1 +h \quad(\because\text{⑥})\\
&=&\dfrac{2\left(V^2-2gh\right)}{g}\cdot\dfrac{(V\sin\theta)^2-2gh}{V^2-2gh}+h \quad(\because\text{①},\text{②})\\
&=&\bbox[6px,border: 2px solid]{\dfrac{2(V\sin\theta)^2}{g}-3h}_\mathbf{\text{ ケ}}
\end{eqnarray}
\end{array}$$

⑵

問題

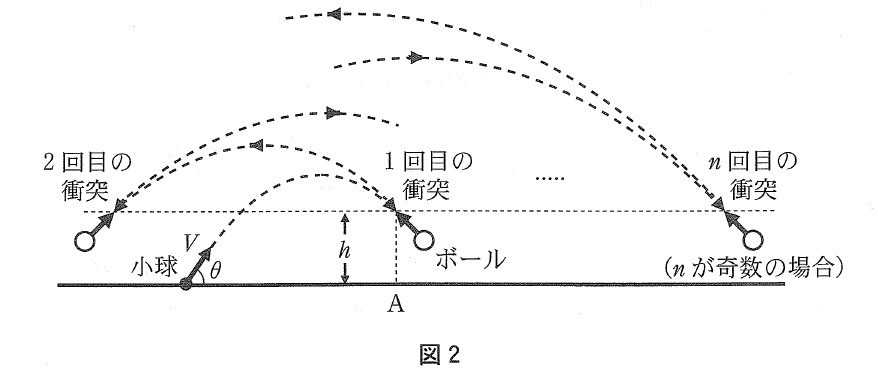
　⑴の小球をさらに高く跳ね上げるため，図2のように，最大高度に到達した後に落下してくる小球めがけて，高度 $h$ でボールを衝突させる，という過程を繰り返し行なったとしよう。ここで，⑴と同様に，小球とボールは一次元的に衝突し，図3のように衝突ごとに定義される衝突軸方向の速度成分を，以下略して「速度成分」と記載する。また $n$ 回目（ $n\geqq 1$ ）の衝突時のボールは，衝突直前の速度の大きさが $V_0$，衝突直後の速度成分 $w_n$ が $0$ となる質量 $M_n$ を有するものとする。

　このとき，$n$ 回目の衝突直後における小球の速度成分 $v_n$ を $a_nV_0$ と表し，衝突が弾性衝突であったとすると，$a_n$ と $a_{n-1}$ の間に，次の関係式が成り立つ。ただし，$n\geqq 2$ とする。
$$a_n=\bbox[3px,border: 2px solid]{~~~~\mathbf{\text{コ}}~~~~}\tag{ⅲ}$$⑴より，$a_1=\bbox[3px,border: 4px double]{~~~~\mathbf{\text{ク}}~~~~}$ であるため，式 $(\text{ⅲ})$ を解いて，$a_n=\bbox[3px,border: 2px solid]{~~~~\mathbf{\text{サ}}~~~~}$ と求まる。これより，$n+1$ 回目の衝突より前に小球が到達する最大高度 $h_n$ は，$h$，$V$，$\theta$，$g$，$n$ を用いて，$h_n=\bbox[3px,border: 2px solid]{~~~~\mathbf{\text{シ}}~~~~}$ となる。

（京都大学）

解答

$n$ 回目の衝突時、衝突直前における小球とボールの速度成分はそれぞれ $-a_{n-1}V_0$、$V_0$ であり、衝突直後における小球とボールの速度成分はそれぞれ $a_nV_0$、$w_n(=0)$ であるから、衝突が弾性衝突であったとき、反発係数の式より
$$\begin{eqnarray}
1&=&-\dfrac{a_nV_0-0}{-a_{n-1}V_0-V_0} \\[0.5em]
a_n&=&\bbox[6px,border: 2px solid]{a_{n-1}+1}_\mathbf{\text{ コ}}\tag{ⅲ}
\end{eqnarray}$$

⑴より $a_1=2$ であり、式 $(\text{ⅲ})$ より数列 $\{a_n\}$ は初項 $2$、公差 $1$ の等差数列となるから、
$$\begin{eqnarray}
a_n=2+(n-1)\cdot 1=\bbox[6px,border: 2px solid]{n+1}_\mathbf{\text{ サ}}\quad\cdots\text{⑦}
\end{eqnarray}$$

よって、$n-1$ 回目の衝突直後の小球の速度成分は $a_{n-1}V_0=nV_0$ であるから、$n-1$ 回目の衝突軸と水平面とのなす角の大きさを $\theta_{n-1}$ とすると、$n-1$ 回目の衝突後の小球の水平方向の速さは $nV_0\cos\theta_{n-1}$ となる。

一方、$n$ 回目の衝突直前の小球の速さを $V_n$ とすると、小球についての「 $n-1$ 回目の衝突直後」と「 $n$ 回目の衝突直前」における力学的エネルギー保存則より
$$\begin{eqnarray}
\dfrac{1}{2}m(nV_0)^2+mgh&=&\dfrac{1}{2}mV_n^2+mgh \\[0.5em]
V_n&=&nV_0\quad\cdots\text{⑧}
\end{eqnarray}$$とわかる。よって、$n$ 回目の衝突軸と水平面とのなす角の大きさを $\theta_n$ とすると、小球の水平方向の速さに関して、次の関係式が成り立つ。
$$\begin{eqnarray}
nV_0\cos\theta_n&=&nV_0\cos\theta_{n-1} \\[0.5em]
\theta_n&=&\theta_{n-1}
\end{eqnarray}$$したがって、帰納的に $\theta_n=\theta_1$ である。

したがって、$n$ 回目の衝突後の小球の運動において、水平方向については速さ $a_nV_0\cos\theta_n$ の等速運動であり、最大高度 $h_n$ において速度の鉛直成分は $0$ であるから、小球についての「 $n$ 回目の衝突直後」と「最大高度 $h_n$ 」における力学的エネルギー保存則より

$$\begin{array}{l}
\dfrac{1}{2}m(a_nV_0)^2+mgh=\dfrac{1}{2}m(a_nV_0\cos\theta_1)^2+mgh_n \\[0.5em]
\begin{eqnarray}
h_n&=&\dfrac{(a_nV_0)^2}{2g}\left(1-\cos^2\theta_1\right)+h \\
&=&\dfrac{(n+1)^2V_0^2}{2g}\sin^2\theta_1 +h \quad(\because\text{⑦})\\
&=&\dfrac{(n+1)^2\left(V^2-2gh\right)}{2g}\cdot\dfrac{(V\sin\theta)^2-2gh}{V^2-2gh}+h \quad(\because\text{①},\text{②})\\
&=&\dfrac{(n+1)^2(V\sin\theta)^2}{2g}-(n+1)^2h+h \\
&=&\bbox[6px,border: 2px solid]{\dfrac{\{(n+1)V\sin\theta\}^2}{2g}-n(n+2)h}_\mathbf{\text{ シ}}\quad\cdots\text{⑨}
\end{eqnarray}
\end{array}$$

問１

問題

　⑵における衝突過程について，以下の問いに答えよ。

(ⅰ)　$n$ 回目に衝突させるボールの質量 $M_n$ は，小球の質量 $m$ の何倍にすればよいか。$n$ を用いて表せ。導出過程も示せ。

(ⅱ)　衝突させるボールの質量に上限があると，衝突直後のボールの速度成分が $0$ となる衝突回数に上限ができる。ボールの質量の上限が小球の質量 $m$ の $10$ 倍である場合，衝突回数が上限に達したときの小球が到達する最大高度は，ボールと衝突する前の最大高度 $h_0$ に比べて何倍になるか，$h=0$ の場合について答えよ。

（京都大学）

解答

(ⅰ)

$n$ 回目の衝突時、衝突直前における小球とボールの速度成分はそれぞれ $-V_n$、$V_0$ であり、衝突直後における小球とボールの速度成分はそれぞれ $a_nV_0$、$0$ であるから、衝突直前直後における運動量保存則より
$$\begin{array}{l}
-mV_n+M_nV_0=ma_nV_0 \\[0.5em]
\begin{eqnarray}
M_n&=&\dfrac{mnV_0}{V_0}+m(n+1)\quad(\because\text{⑦},\text{⑧}) \\
&=& (2n+1)m
\end{eqnarray}
\end{array}$$となるから、$M_n$ は $m$ の $\style{border-bottom:double 4px;padding-bottom:3px}{\boldsymbol{2n+1} \ \mathbf{\text{倍}}}$ にすればよい。

(ⅱ)

(ⅰ)より
$$M_n=(2n+1)m\leqq 10m \quad \Longleftrightarrow \quad n\leqq 4.5$$となるから、衝突回数の上限は $4$ 回である。

ここで、ボールと衝突する前において、小球の「投げ上げた直後」と「最大高度 $h_0$ に達したとき」の鉛直方向の速度はそれぞれ $V\sin\theta$、$0$ であるから、等加速度直線運動の公式より
$$\begin{eqnarray}
0^2-(V\sin\theta)^2&=&-2gh_0 \\
h_0 &=& \dfrac{(V\sin\theta)^2}{2g}
\end{eqnarray}$$とわかる。

また $\text{⑨}$ と $h=0$ より、$n+1$ 回目の衝突より前に小球が到達する最大高度 $h_n$ は
$$h_n=\dfrac{\{(n+1)V\sin\theta\}^2}{2g}=(n+1)^2h_0$$となるから、$5$ 回目の衝突より前に小球が到達する最大高度 $h_4$ は
$$h_4=25h_0$$となる。

したがって、衝突回数が上限に達したときの小球が到達する最大高度は $h_0$ の $\style{border-bottom:double 4px;padding-bottom:3px}{\mathbf{25} \ \mathbf{\text{倍}}}$ である。

答え一覧

⑴
$$\begin{array}{l}
\bbox[3px,border: 2px solid]{~~~~\mathbf{\text{ア}}~~~~}\cdots \sqrt{ V^2-2gh }\\[0.5em]
\bbox[3px,border: 2px solid]{~~~~\mathbf{\text{イ}}~~~~}\cdots \sqrt{\dfrac{(V\sin\theta)^2-2gh}{V^2-2gh}}\\[0.5em]
\bbox[3px,border: 2px solid]{~~~~\mathbf{\text{ウ}}~~~~}\cdots -mV_0+MV_0\\[0.5em]
\bbox[3px,border: 2px solid]{~~~~\mathbf{\text{エ}}~~~~}\cdots -2V_0\\[0.5em]
\bbox[3px,border: 2px solid]{~~~~\mathbf{\text{オ}}~~~~}\cdots \dfrac{3M-m}{m+M}V_0\\[0.5em]
\bbox[3px,border: 2px solid]{~~~~\mathbf{\text{カ}}~~~~}\cdots \dfrac{M-3m}{m+M}V_0\\[0.5em]
\bbox[3px,border: 2px solid]{~~~~\mathbf{\text{キ}}~~~~}\cdots 3\\[0.5em]
\bbox[3px,border: 2px solid]{~~~~\mathbf{\text{ク}}~~~~}\cdots 2\\[0.5em]
\bbox[3px,border: 2px solid]{~~~~\mathbf{\text{ケ}}~~~~}\cdots \dfrac{2(V\sin\theta)^2}{g}-3h
\end{array}$$

⑵
$$\begin{array}{l}
\bbox[3px,border: 2px solid]{~~~~\mathbf{\text{コ}}~~~~}\cdots a_{n-1}+1\\[0.5em]
\bbox[3px,border: 2px solid]{~~~~\mathbf{\text{サ}}~~~~}\cdots n+1\\[0.5em]
\bbox[3px,border: 2px solid]{~~~~\mathbf{\text{シ}}~~~~}\cdots \dfrac{\{(n+1)V\sin\theta\}^2}{2g}-n(n+2)h
\end{array}$$

問１
(ⅰ)
運動量保存則より
$$\begin{eqnarray}
-mnV_0+M_nV_0&=&m(n+1)V_0 \\
M_n&=&(2n+1)m
\end{eqnarray}$$よって、$\style{border-bottom:double 4px;padding-bottom:3px}{\boldsymbol{2n+1} \ \mathbf{\text{倍}}}$
(ⅱ)
$$(2n+1)m\leqq 10m \quad \Longleftrightarrow \quad n\leqq 4.5$$より、衝突回数の上限は $4$ 回である。
ここで $h_0=\dfrac{(V\sin\theta)^2}{2g}$ であり、$h=0$ のとき
$$h_n=\dfrac{\{(n+1)V\sin\theta\}^2}{2g}=(n+1)^2h_0$$ より、最大高度 $h_4$ は
$$h_4=25h_0$$よって、$\style{border-bottom:double 4px;padding-bottom:3px}{\boldsymbol{25} \ \mathbf{\text{倍}}}$

まとめ

今回は、京都大学理系数学（2021年 問題Ⅰ）の解説をしました。