今回は、大阪大学理系数学(2022年 第3問)の解説をしたいと思います。
問題
正の実数 $t$ に対し,座標平面上の $2$ 点 $\mathrm{P}(0,t)$ と $\mathrm{Q}\left(\dfrac{1}{t},0\right)$ を考える.$t$ が $1 \leqq t\leqq 2$ の範囲を動くとき,座標平面内で線分 $\mathrm{PQ}$ が通過する部分を図示せよ.
(大阪大学)
解答
線分 $\mathrm{PQ}$ の方程式は
$$y=\dfrac{0-t}{\dfrac{1}{t}-0}x+t \quad (x\geqq 0, \ y\geqq 0)$$より
$$y=-t^2x+t \quad (x\geqq 0, \ y\geqq 0) \quad \cdots \text{①}$$
$x \ (\geqq 0)$ を固定し、$t$ を $1 \leqq t\leqq 2$ の範囲で動かしたときの $y$ の値域を調べる。
(ⅰ) $x=0$ のとき
①より $y=x$ であり、$1 \leqq t\leqq 2$ より
$$1 \leqq y\leqq 2$$
(ⅱ) $x\gt 0$ のとき
①より $y=-x\left(t-\dfrac{1}{2x}\right)^2+\dfrac{1}{4x}$($=f(t)$ とおく)
(ア) $2\leqq\dfrac{1}{2x}$ すなわち $x\leqq\dfrac{1}{4}$ のとき
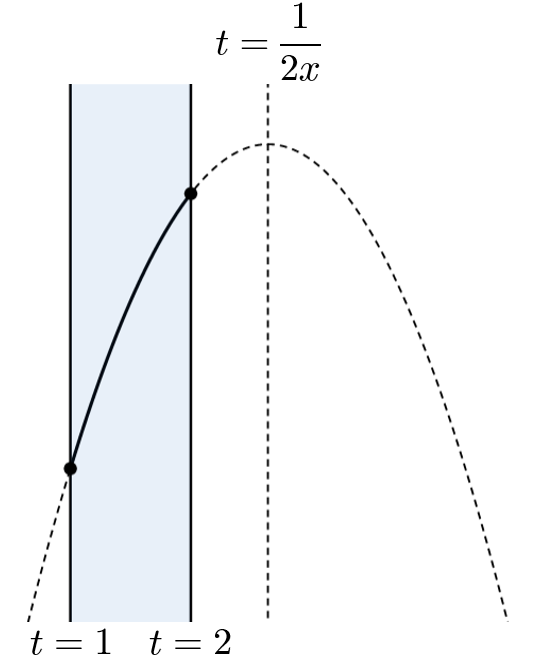
$f(1)\leqq y\leqq f(2)$ より
$$-x+1\leqq y\leqq -4x+2$$
(イ) $\dfrac{3}{2}\leqq\dfrac{1}{2x}\lt 2$ すなわち $\dfrac{1}{4}\lt x\leqq\dfrac{1}{3}$ のとき
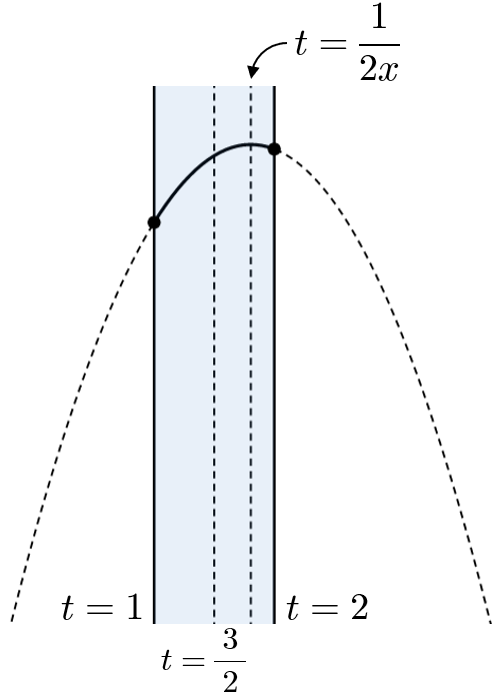
$f(1)\leqq y\leqq f\left(\dfrac{1}{2x}\right)$ より
$$-x+1\leqq y\leqq \dfrac{1}{4x}$$
(ウ) $1\leqq\dfrac{1}{2x}\lt \dfrac{3}{2}$ すなわち $\dfrac{1}{3}\lt x\leqq\dfrac{1}{2}$ のとき
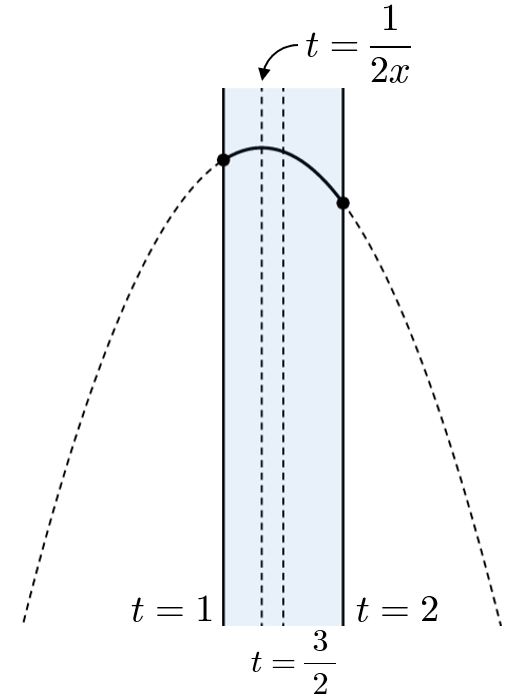
$f(2)\leqq y\leqq f\left(\dfrac{1}{2x}\right)$ より
$$-4x+2\leqq y\leqq \dfrac{1}{4x}$$
(エ) $\dfrac{1}{2x}\lt 1$ すなわち $\dfrac{1}{2}\lt x$ のとき
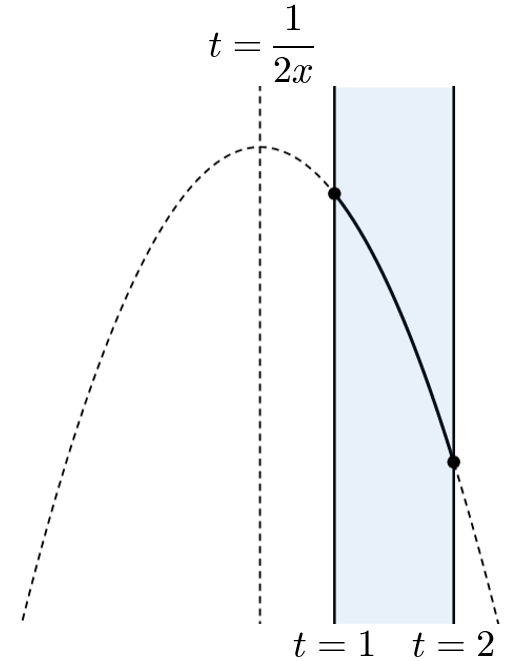
$f(2)\leqq y\leqq f(1)$ より
$$-4x+2\leqq y\leqq -x+1$$
(ⅰ),(ⅱ)と $y \geqq 0$ より、求める領域は下図の網掛け部分である。ただし、境界線を含む。
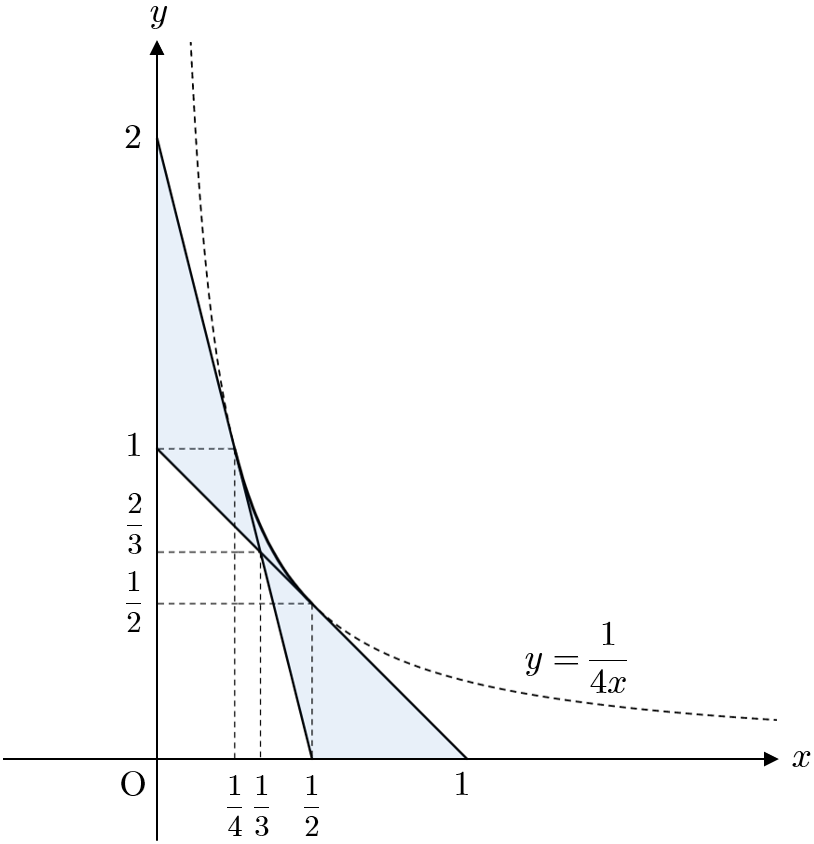
下図の網掛け部分(境界線を含む)

解説
いわゆる「ファクシミリの原理」を使って解く通過領域の問題です。
どの文字を固定し、どの文字を(どこからどこまで)動かすのかをしっかりと確認しながら解き進めましょう。
2次関数の最大・最小は軸と定義域に注意しましょう。
まとめ
今回は、大阪大学理系数学(2022年 第3問)の解説をしました。
ほかの問題にもチャレンジしよう!
大阪大学 理系数学 2022年 第1問 解説
大阪大学 理系数学 2022年 第2問 解説
大阪大学 理系数学 2022年 第3問 解説
大阪大学 理系数学 2022年 第4問 解説
大阪大学 理系数学 2022年 第5問 解説













