今回は、東京大学理系数学(2020年 第5問)の解説をしたいと思います。
問題
座標空間において,$xy$ 平面上の原点を中心とする半径 $1$ の円を考える。この円を底面とし,点 $(0,0,2)$ を原点とする円錐(内部を含む)を $S$ とする。また,点 $\mathrm{A}(1,0,2)$ を考える。
⑴ 点 $\mathrm{P}$ が $S$ の底面を動くとき,線分 $\mathrm{AP}$ が通過する部分を $T$ とする。平面 $z=1$ による $S$ の切り口および,平面 $z=1$ による $T$ の切り口を同一平面上に図示せよ。
⑵ 点 $\mathrm{P}$ が $S$ を動くとき,線分 $\mathrm{AP}$ が通過する部分の体積を求めよ。
(東京大学)
解答
⑴
原点を $\mathrm{O}$ とし、$(0,0,2)$ の点を $\mathrm{B}$ とする。
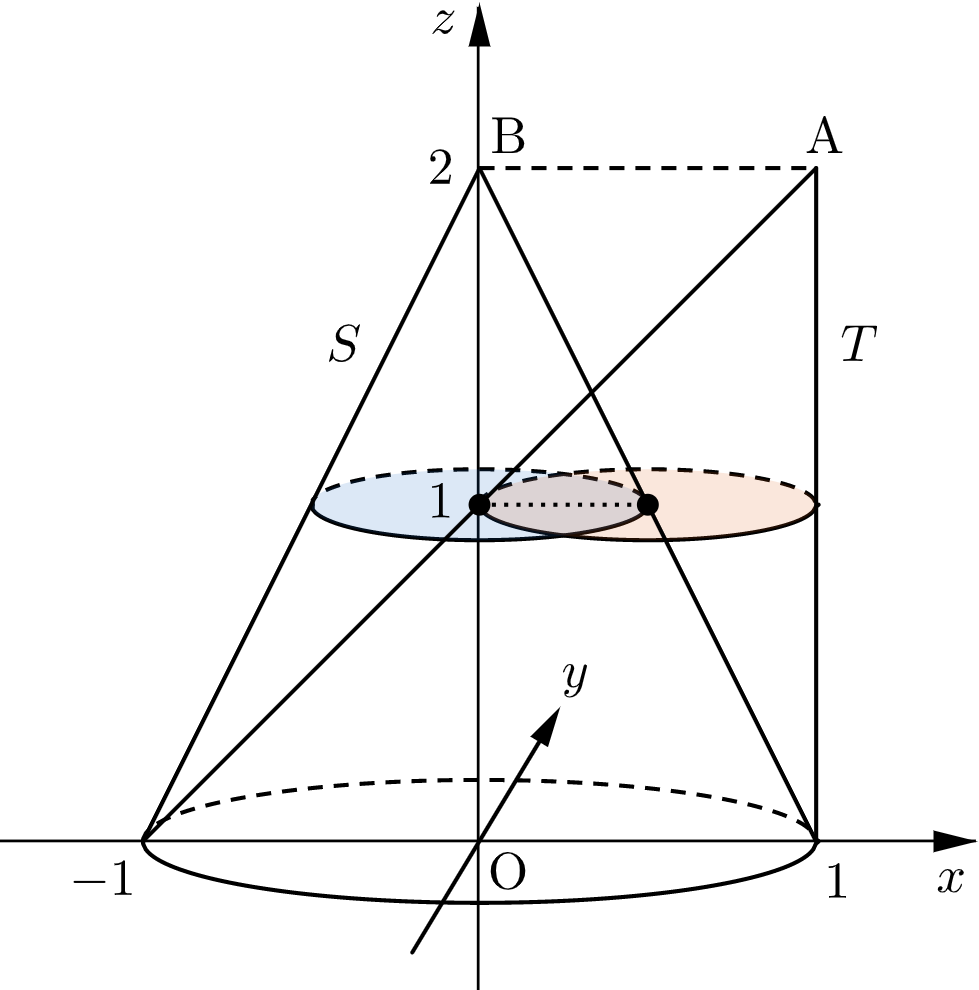
点 $\mathrm{P}$ が $S$ の底面の原点を除く範囲を動くとき、$\mathrm{P}$ の座標は $0\leqq r\leqq 1, \ $$0\leqq\theta\leqq 2\pi$ を満たす実数 $r,\theta$ を用いて $(r\cos\theta, \ r\sin\theta , \ 0)$ と表せる。
ここで、線分 $\mathrm{BP}$ 上の点を $\mathrm{Q}$ とすると、$0\leqq s\leqq 1$ を満たす実数 $s$ を用いて
$$\begin{align}
\overrightarrow{\mathrm{OQ}} &= \overrightarrow{\mathrm{OB}} +s\overrightarrow{\mathrm{BQ}} \\
&=
\begin{pmatrix}
0 \\ 0 \\ 2
\end{pmatrix}
+s
\begin{pmatrix}
r\cos\theta \\ r\sin\theta \\ -2
\end{pmatrix}\quad\cdots\text{①}
\end{align}$$と表せる。$\mathrm{Q}$ が平面 $z=1$ 上の点となるのは $2-2s=1$ すなわち $s=\dfrac{1}{2}$ のときであり、このとき
$$\overrightarrow{\mathrm{OQ}} =
\begin{pmatrix}
0 \\ 0 \\ 1
\end{pmatrix}
+\dfrac{r}{2}
\begin{pmatrix}
\cos\theta \\ \sin\theta \\ 0
\end{pmatrix}$$となるので、点 $\mathrm{Q}$ は平面 $z=1$ 上で点 $(0,0,1)$ を中心とする半径 $\dfrac{1}{2}$ の円の周および内部を動き、これが平面 $z=1$ による $S$ の切り口 $S’$ である。
また、線分 $\mathrm{AP}$ 上の点を $\mathrm{R}$ とすると、$0\leqq t\leqq 1$ を満たす実数 $t$ を用いて
$$\begin{align}
\overrightarrow{\mathrm{OR}} &= \overrightarrow{\mathrm{OA}} +t\overrightarrow{\mathrm{AR}} \\
&=
\begin{pmatrix}
1 \\ 0 \\ 2
\end{pmatrix}
+t
\begin{pmatrix}
r\cos\theta-1 \\ r\sin\theta \\ -2
\end{pmatrix}
\end{align}$$と表せる。$\mathrm{R}$ が平面 $z=1$ 上の点となるのは $2-2t=1$ すなわち $t=\dfrac{1}{2}$ のときであり、このとき
$$\overrightarrow{\mathrm{OR}} =
\begin{pmatrix}
\dfrac{1}{2} \\ 0 \\ 1
\end{pmatrix}
+\dfrac{r}{2}
\begin{pmatrix}
\cos\theta \\ \sin\theta \\ 0
\end{pmatrix}$$となるので、点 $\mathrm{R}$ は平面 $z=1$ 上で点 $\left(\dfrac{1}{2}, \ 0, \ 1\right)$ を中心とする半径 $\dfrac{1}{2}$ の円の周および内部を動き、これが平面 $z=1$ による $T$ の切り口 $T’$ である。
したがって、$(0,0,1)$ の点を $\mathrm{O}’$ とすると、$S’,T’$ は下図の網掛け部分となる。ただし、境界を含む。
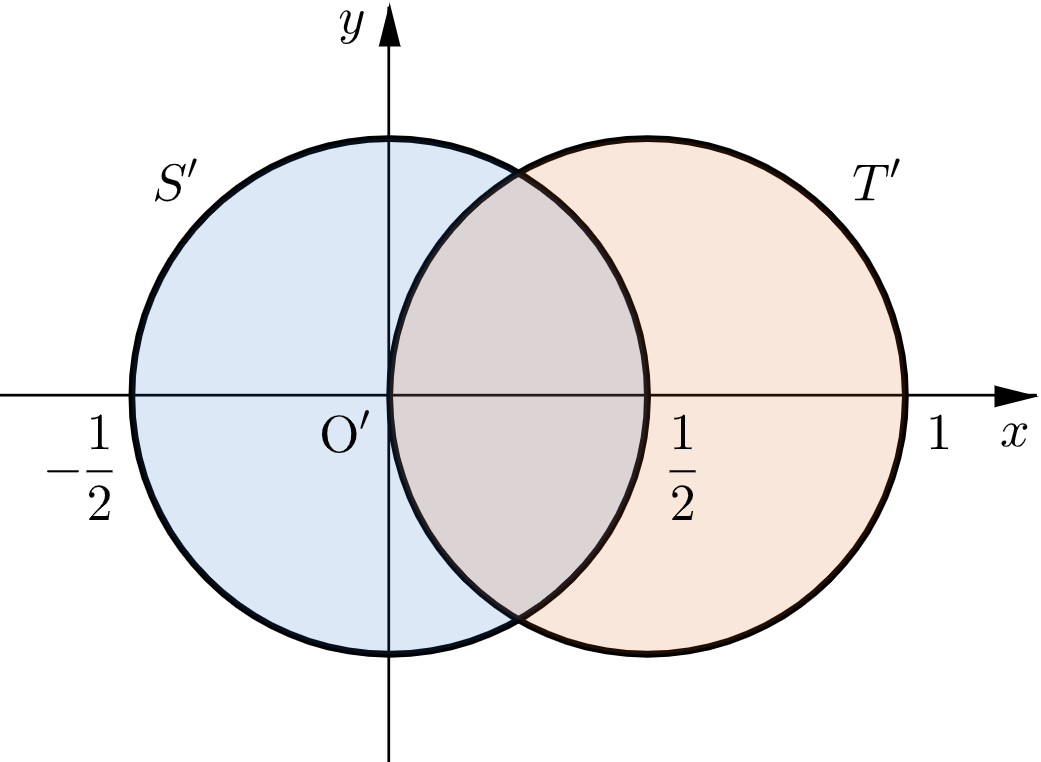
下図の網掛け部分(境界を含む)

⑵
点 $\mathrm{P}$ が $S$ を動くとき、線分 $\mathrm{AP}$ が通過する部分を $W$ とおく。
平面 $z=k$( $0\leqq k \lt 2$ )による $S$ の切り口 $S_k$ について考える。
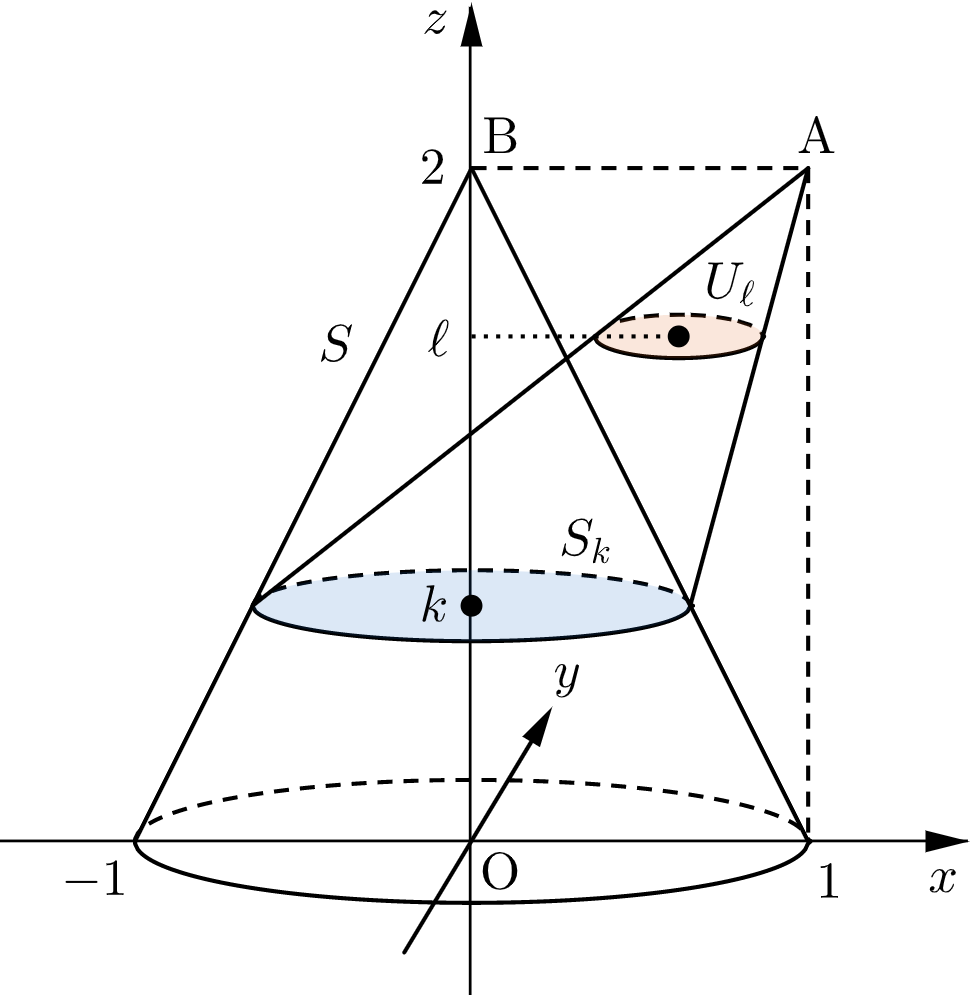
線分 $\mathrm{BP}$ 上の点 $\mathrm{Q}$ が平面 $z=k$ 上の点となるのは、①より $2-2s=k$ すなわち $s=\dfrac{2-k}{2}$ のときであり、このとき
$$\overrightarrow{\mathrm{OQ}} =
\begin{pmatrix}
0 \\ 0 \\ k
\end{pmatrix}
+\dfrac{2-k}{2}r
\begin{pmatrix}
\cos\theta \\ \sin\theta \\ 0
\end{pmatrix}$$となるので、点 $\mathrm{Q}$ は平面 $z=k$ 上で点 $(0,0,k)$ を中心とする半径 $\dfrac{2-k}{2}$ の円の周および内部を動き、これが $S_k$ である。
すなわち、$S_k$ 上の点 $\mathrm{P}$ の座標は $0\leqq r’\leqq \dfrac{2-k}{2}, \ $$0\leqq\theta’\leqq 2\pi$ を満たす実数 $r’,\theta’$ を用いて $(r’\cos\theta’, \ r’\sin\theta’ , \ k)$ と表せる。
点 $\mathrm{P}$ が $S_k$ を動くとき、線分 $\mathrm{AP}$ が通過する部分の平面 $z=\ell$( $k\leqq \ell \leqq 2$ )による切り口 $U_\ell$ について考える。
線分 $\mathrm{AP}$ 上の点を $\mathrm{R}’$ とすると、$0\leqq u\leqq 1$ を満たす実数 $u$ を用いて
$$\begin{align}
\overrightarrow{\mathrm{OR}’} &= \overrightarrow{\mathrm{OA}} +u\overrightarrow{\mathrm{AR}’} \\
&=
\begin{pmatrix}
1 \\ 0 \\ 2
\end{pmatrix}
+u
\begin{pmatrix}
r’\cos\theta’-1 \\ r’\sin\theta’ \\ k-2
\end{pmatrix}
\end{align}$$と表せる。$\mathrm{R}’$ が平面 $z=\ell$ 上の点となるのは $2+u(k-2)=\ell$ すなわち $u=\dfrac{2-\ell}{2-k}$ のときであり、このとき
$$\overrightarrow{\mathrm{OR}’} =
\begin{pmatrix}
\dfrac{\ell-k}{2-k} \\ 0 \\ \ell
\end{pmatrix}
+\dfrac{2-\ell}{2-k}r’
\begin{pmatrix}
\cos\theta’ \\ \sin\theta’ \\ 0
\end{pmatrix}$$となる。
$0\leqq r’\leqq \dfrac{2-k}{2}$ より $0\leqq \dfrac{2-\ell}{2-k}r’ \leqq \dfrac{2-\ell}{2}$ なので、点 $\mathrm{R}’$ は平面 $z=\ell$ 上で点 $\left(\dfrac{\ell-k}{2-k}, \ 0, \ \ell\right)$ を中心とする半径 $\dfrac{2-\ell}{2}$ の円の周および内部を動き、これが $U_\ell$ である。
$k$ が $0\leqq k \leqq \ell$ の範囲を動くとき、$U_\ell$ の中心の $x$ 座標は $0\leqq \dfrac{\ell-k}{2-k} \leqq \dfrac{\ell}{2}$ の範囲を動く。また $y$ 座標、$z$ 座標についてはそれぞれ $0,\ell$ で一定であり、半径も $\dfrac{2-\ell}{2}$ で一定である。
したがって、$(0,0,\ell)$ の点を $\mathrm{O}_\ell$ とすると、$0\leqq k \leqq \ell$ において点 $\mathrm{P}$ が $S_k$ を動くとき、$U_\ell$ は下図の網掛け部分を動く。
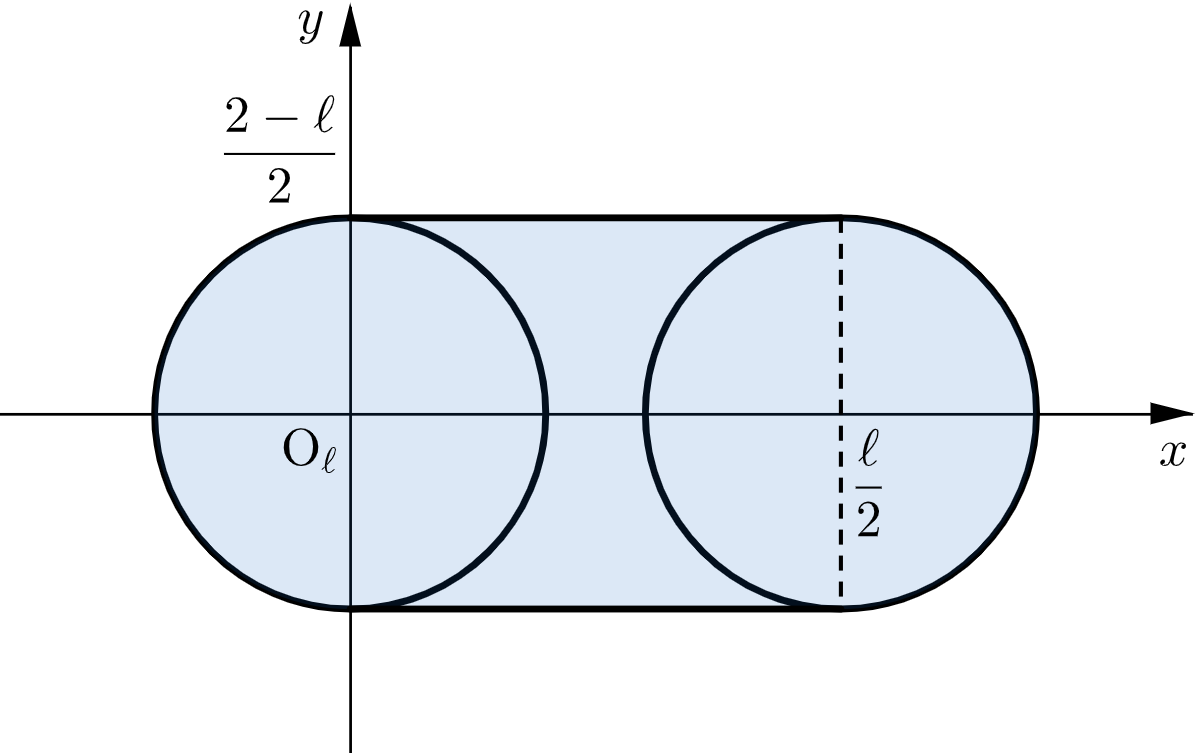
これが平面 $z=\ell$ による $W$ の切り口であり、その面積 $f(\ell)$ は、長方形と円の面積を足せばよいので
$$\begin{align}
f(\ell) &= 2 \cdot \dfrac{2-\ell}{2} \cdot \dfrac{\ell}{2} + \pi\left( \dfrac{2-\ell}{2} \right)^2 \\
&= \dfrac{\ell(2-\ell)}{2} + \dfrac{\pi(2-\ell)^2}{4} \ \text{(} \ 0\leqq\ell\leqq 2 \ \text{)}
\end{align}$$
したがって、求める体積 $V$ は
$$\begin{align}
V &= \displaystyle\int_{0}^{2}f(\ell)d\ell \\
&= \displaystyle\int_{0}^{2} \left\{ \dfrac{\ell(2-\ell)}{2} + \dfrac{\pi(2-\ell)^2}{4} \right\} d\ell \\
&= \dfrac{1}{2}\cdot\dfrac{(2-0)^3}{6}+\dfrac{\pi}{4}\left[ -\dfrac{(2-\ell)^3}{3} \right]_0^2 \\
&= \boldsymbol{ \dfrac{2}{3} + \dfrac{2}{3}\pi }
\end{align}$$
$$\boldsymbol{ \dfrac{2}{3} + \dfrac{2}{3}\pi }$$
解説
⑴は答えだけ求めればよいなら簡単ですが、過程を記述しなければならないので面倒です。
解答のようにベクトルで処理するか、三角形の相似に着目するのがベターです。
図示問題なので、図さえ合っていれば記述はほどほどで大丈夫です。
⑵は、まず「 $S$ を動く」を「 $S$ の底面を動く」と誤読しないよう注意しましょう。
また、よく分からない立体の体積を求めるときは、ある平面で切って断面積を求めて積分するという流れが定番です。
今回の問題では、その「ある平面で切った断面」が別の変数(解答では $k$ )が動くことでややこしくなっています。
「平面 $z=\ell$ で切った断面」を求めるために、平面 $z=\ell$ より下側の $S$ を点 $\mathrm{P}$ が動くときの「線分 $\mathrm{AP}$ と平面 $z=\ell$ の交点」が動く範囲を考えなければならない、という流れです。
まとめ
今回は、東京大学理系数学(2020年 第5問)の解説をしました。
ほかの問題にもチャレンジしよう!
東京大学 理系数学 2020年 第1問 解説
東京大学 理系数学 2020年 第2問 解説
東京大学 理系数学 2020年 第3問 解説
東京大学 理系数学 2020年 第4問 解説
東京大学 理系数学 2020年 第5問 解説
東京大学 理系数学 2020年 第6問 解説













