東京大学 理系数学 2020年 第2問 解説

今回は、東京大学理系数学（2020年 第2問）の解説をしたいと思います。

問題

　平面上の点 $\mathrm{P},\mathrm{Q},\mathrm{R}$ が同一直線上にないとき，それらを $3$ 頂点とする三角形の面積を $\triangle\mathrm{PQR}$ で表す。また，$\mathrm{P},\mathrm{Q},\mathrm{R}$ が同一直線上にあるときは，$\triangle\mathrm{PQR}=0$ とする。

　$\mathrm{A},\mathrm{B},\mathrm{C}$ を平面上の $3$ 点とし，$\triangle\mathrm{ABC}=1$ とする。この平面上の点 $\mathrm{X}$ が
$$2 \leqq \triangle\mathrm{ABX} + \triangle\mathrm{BCX} + \triangle\mathrm{CAX} \leqq 3$$を満たしながら動くとき，$\mathrm{X}$ の動きうる範囲の面積を求めよ。

（東京大学）

解答

$$S=\triangle\mathrm{ABX} + \triangle\mathrm{BCX} + \triangle\mathrm{CAX}$$とおくと、点 $\mathrm{X}$ は
$$2\leqq S \leqq 3$$ を満たしながら動く。

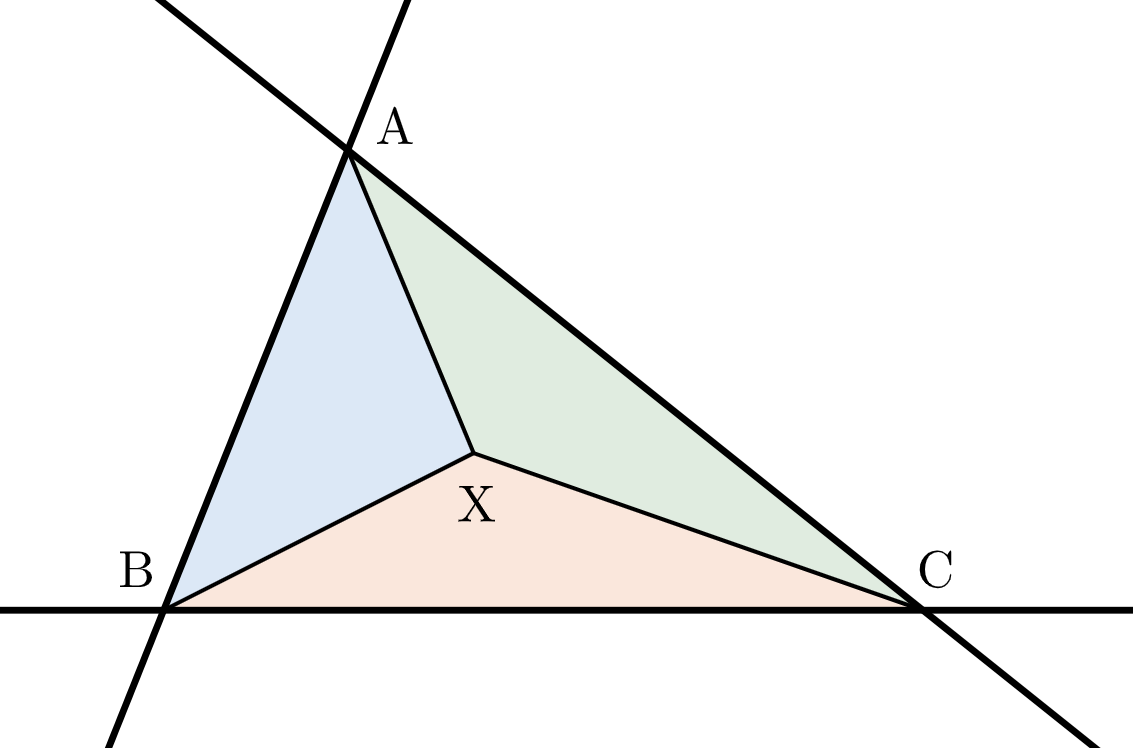
点 $\mathrm{X}$ が三角形 $\mathrm{ABC}$ の周および内部にある場合
$$S=\triangle\mathrm{ABC}=1$$より、$2 \leqq S \leqq 3$ を満たさない。

よって、点 $\mathrm{X}$ が三角形 $\mathrm{ABC}$ の外部にある場合を考える。

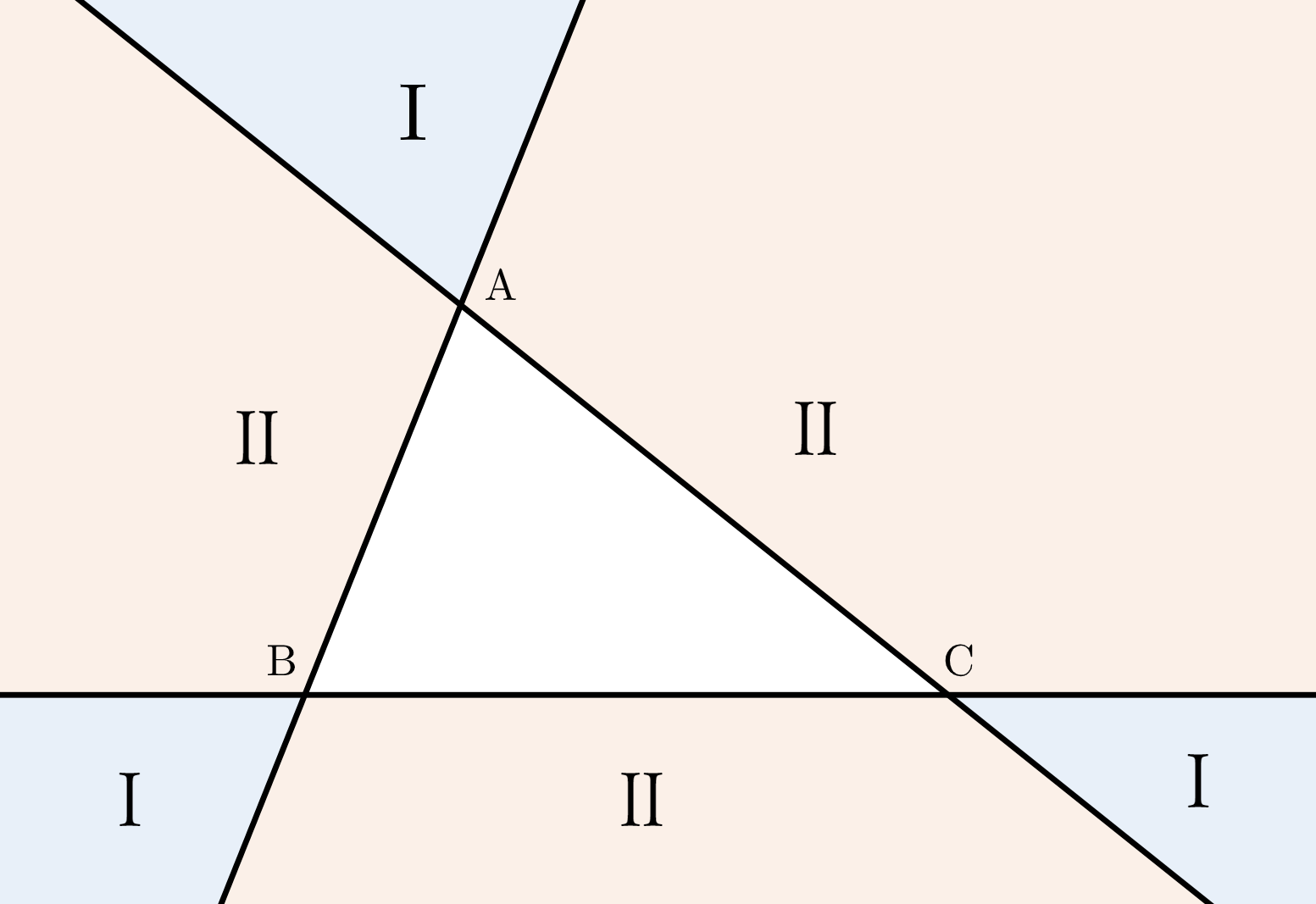
このとき、図のように、三角形 $\mathrm{ABC}$ の外部を直線 $\mathrm{AB},\mathrm{BC},\mathrm{CA}$ で区切られた $6$ 個の領域に分け、これらを
$$\left\{\begin{align}
\text{領域Ⅰ} &\cdots \ 2 \ \text{本の直線で形成される領域} \\
\text{領域Ⅱ} &\cdots \ 3 \ \text{本の直線で形成される領域}
\end{align}\right.$$の $2$ つに分類する。ただし、境界は両方の領域に属するものとする。

(ⅰ)　点 $\mathrm{X}$ が領域Ⅰにある場合

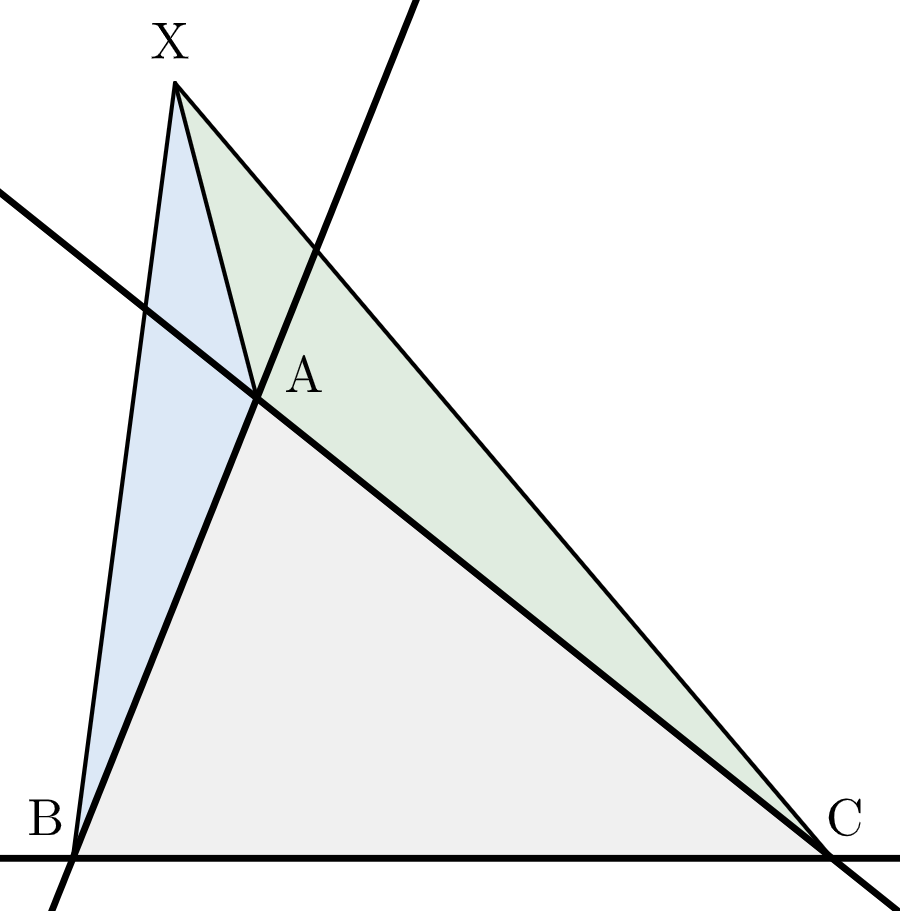
図のように、$\mathrm{A}$ を頂点とする領域Ⅰにある場合を考えると
$$S+\triangle\mathrm{ABC} = 2\triangle\mathrm{BCX}$$が成り立つ。$\triangle\mathrm{ABC}=1$ より、点 $\mathrm{X}$ は
$$\dfrac{3}{2} \leqq \triangle\mathrm{BCX} \leqq 2$$を満たしながら動く。

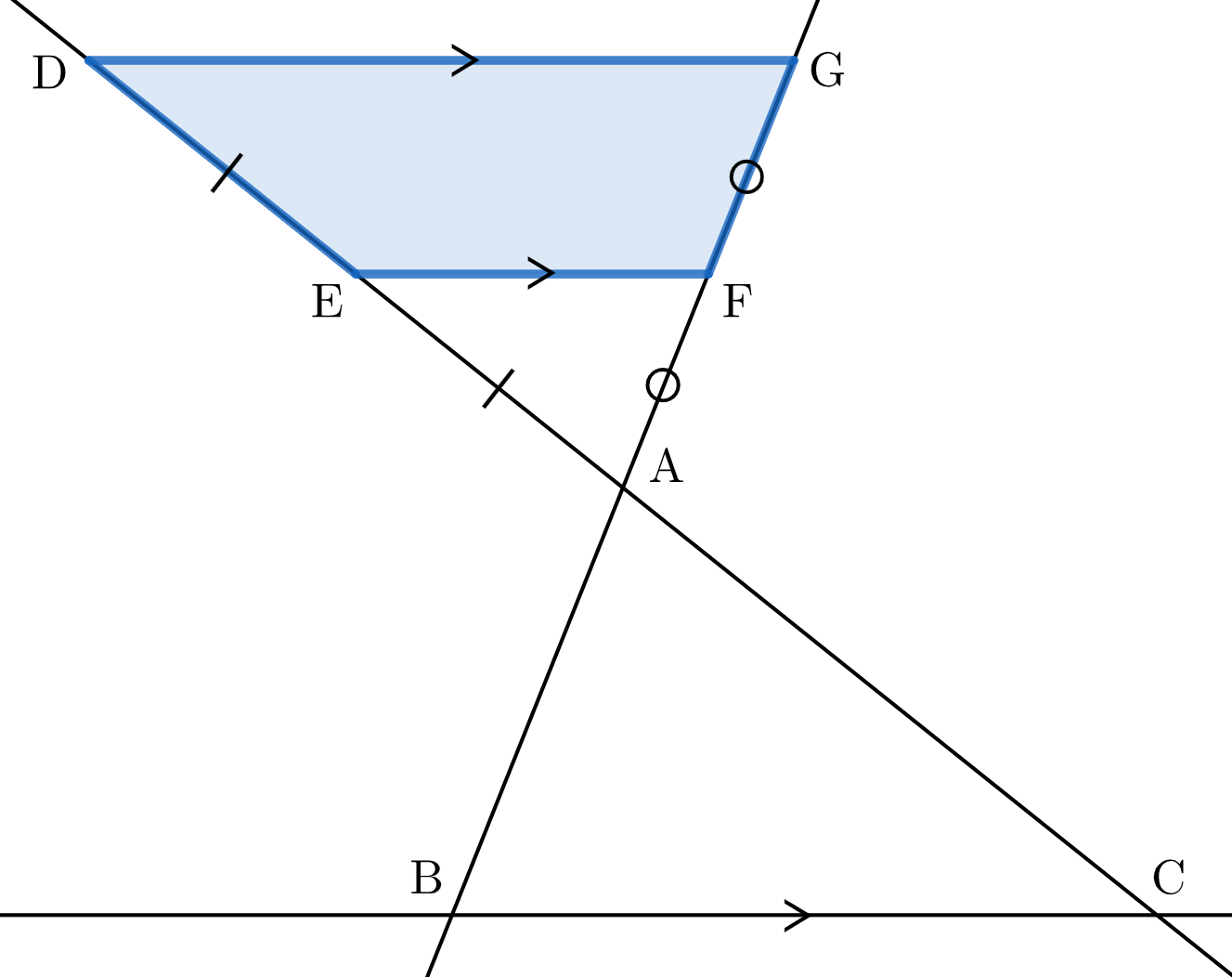
このとき、三角形 $\mathrm{BCX}$ の辺 $\mathrm{BC}$ からの高さを考えると、点 $\mathrm{X}$ は図の台形 $\mathrm{DEFG}$ の周および内部を動く。ただし
$$\left\{\begin{array}{l}
\mathrm{DE}=\mathrm{EA}=\dfrac{1}{2}\mathrm{CA} \\
\mathrm{GF}=\mathrm{FA}=\dfrac{1}{2}\mathrm{AB}
\end{array}\right.$$を満たす。

$\triangle\mathrm{AGD}=\triangle\mathrm{ABC}=1$ であり、$\triangle\mathrm{AGD}$ と $\triangle\mathrm{AFE}$ の相似比は $2:1$ なので
$$\begin{align}
(\text{台形} \ \mathrm{DEFG} \ \text{の面積}) &= \triangle\mathrm{AGD}-\triangle\mathrm{AFE} \\
&= 1-\dfrac{1}{2^2} = \dfrac{3}{4}
\end{align}$$

同様に、他の $2$ 個の領域Ⅰにおける点 $\mathrm{X}$ の存在範囲の面積もそれぞれ $\dfrac{3}{4}$ である。

(ⅱ)　点 $\mathrm{X}$ が領域Ⅱにある場合

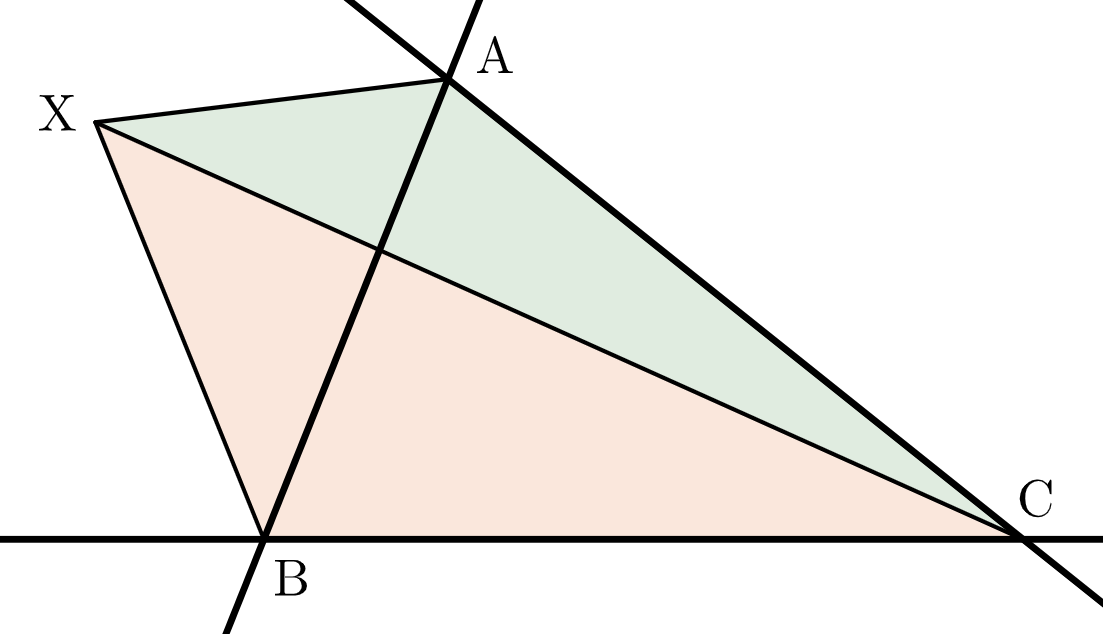
図のように、辺 $\mathrm{AB}$ を境界とする領域Ⅱにある場合を考えると
$$S-\triangle\mathrm{ABC} = 2\triangle\mathrm{ABX}$$が成り立つ。$\triangle\mathrm{ABC}=1$ より、点 $\mathrm{X}$ は
$$\dfrac{1}{2} \leqq \triangle\mathrm{ABX} \leqq 1$$を満たしながら動く。

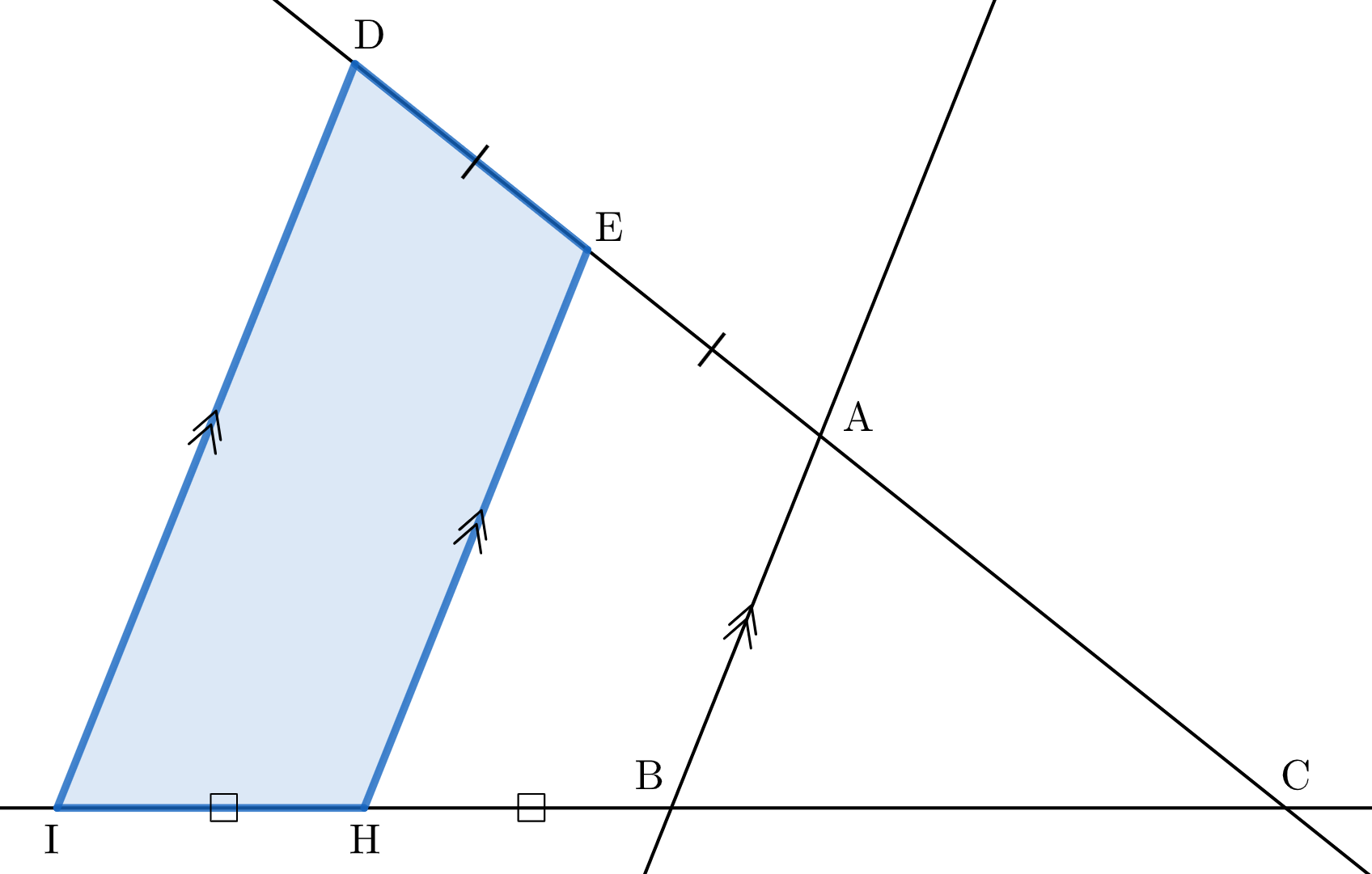
このとき、三角形 $\mathrm{ABX}$ の辺 $\mathrm{AB}$ からの高さを考えると、点 $\mathrm{X}$ は図の台形 $\mathrm{DEHI}$ の周および内部を動く。ただし、$\mathrm{D},\mathrm{E}$ は(ⅰ)と同じ点であり
$$\mathrm{IH}=\mathrm{HB}=\dfrac{1}{2}\mathrm{BC}$$を満たす。

$\triangle\mathrm{CAB}$ と $\triangle\mathrm{CEH}$ と $\triangle\mathrm{CDI}$ の相似比は $1:\dfrac{3}{2}:2$ なので
$$\begin{align}
(\text{台形} \ \mathrm{DEHI} \ \text{の面積}) &= \triangle\mathrm{CDI}-\triangle\mathrm{CEH} \\
&= 2^2-\left(\dfrac{3}{2}\right)^2 = \dfrac{7}{4}
\end{align}$$

同様に、他の $2$ 個の領域Ⅱにおける点 $\mathrm{X}$ の存在範囲の面積もそれぞれ $\dfrac{7}{4}$ である。

(ⅰ),(ⅱ)より、$\mathrm{X}$ の動きうる範囲の面積は
$$3\cdot\left( \dfrac{3}{4}+\dfrac{7}{4} \right) = \boldsymbol{\dfrac{15}{2}}$$

解説

設定が抽象的なので、座標平面で解きたい気持ちも出てきますが、点の座標を文字で表したうえで、面積について考察しなければならないので、だいぶ煩雑です。
また、ベクトルや三角比なども頭をよぎりますが、ここは幾何で解ききる覚悟を決めましょう。

点 $\mathrm{X}$ の存在範囲に領域Ⅰ・Ⅱの $2$ パターンがあると気づければ、相似・平行を利用して面積を求めましょう。

ちなみに、点 $\mathrm{X}$ の存在範囲を図示すると、下図の網掛け部分（境界を含む）のようになります。

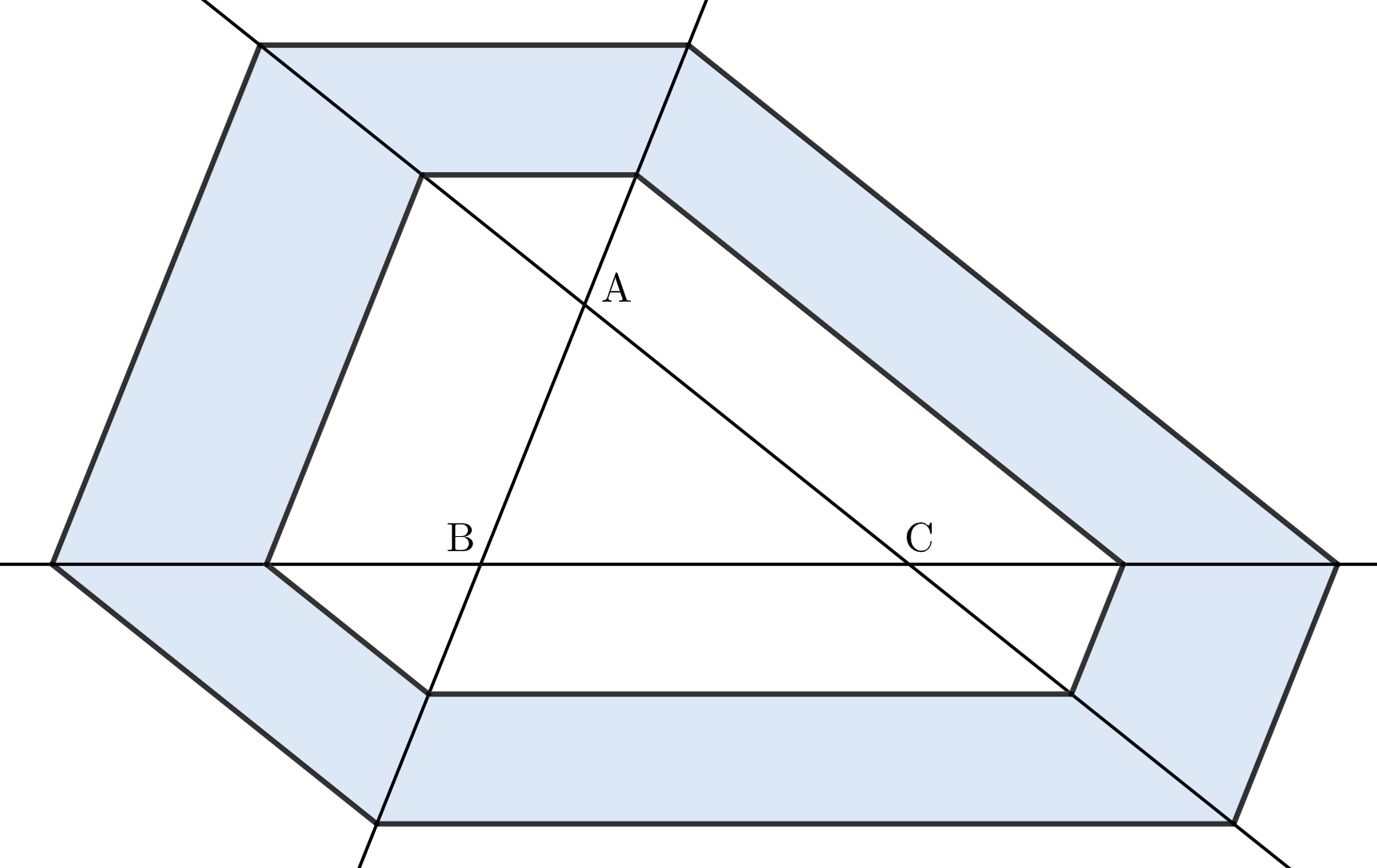
まとめ

今回は、東京大学理系数学（2020年 第2問）の解説をしました。