大阪大学 理系数学 2020年 第4問 解説

今回は、大阪大学理系数学（2020年 第4問）の解説をしたいと思います。

問題

　$t$ を正の実数とする．$xy$ 平面において，連立不等式
$$x\geqq0,\quad y\geqq0,\quad xy\leqq1,\quad x+y\leqq t$$の表す領域の面積を $S(t)$ とおく．極限 $\displaystyle\lim_{t\to\infty}\big(S(t)-2\log t\big)$ を求めよ．

（大阪大学）

解答

与連立不等式が表す領域は下図の網掛け部分である。

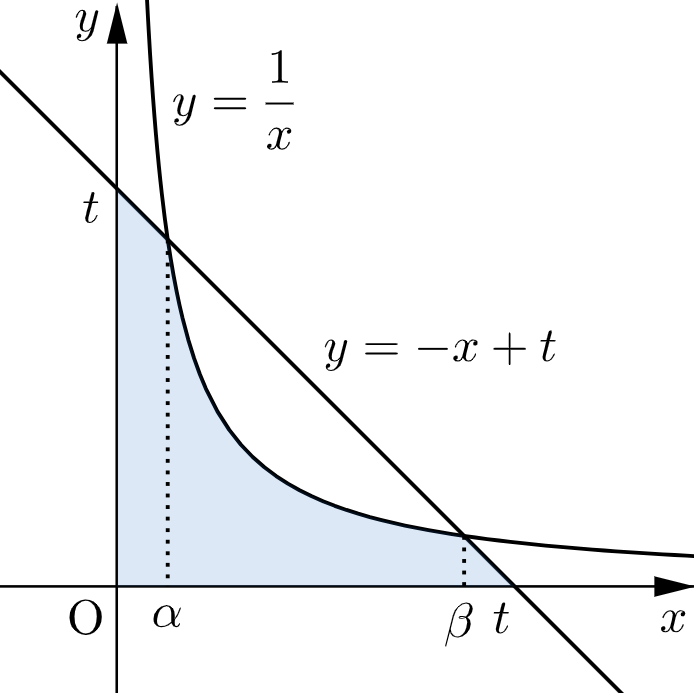
$y=\dfrac{1}{x}$ と $y=-x+t$ から $y$ を消去して整理すると
$$x^2-tx+1=0$$となり、この解を $\alpha,\,\beta \ $$(\alpha\lt\beta)$ とすると
$$\alpha=\dfrac{t-\sqrt{t^2-4}}{2},\quad\beta=\dfrac{t+\sqrt{t^2-4}}{2}$$となる。

よって
$$\begin{align}
S(t) &= \dfrac{1}{2}\cdot t\cdot t-\displaystyle\int_{\alpha}^{\beta}\left(-x+t-\dfrac{1}{x}\right)dx \\
&= \dfrac{t^2}{2}-\left[-\dfrac{x^2}{2}+tx-\log x\right]_{\alpha}^{\beta} \\
&= \dfrac{t^2}{2}+\dfrac{1}{2}(\beta^2-\alpha^2)-t(\beta-\alpha)+\log\beta-\log\alpha \\
&= \dfrac{t^2}{2}+\dfrac{1}{2}(\beta+\alpha)(\beta-\alpha)-t(\beta-\alpha)+\log\dfrac{\beta}{\alpha} \\
&= \dfrac{t^2}{2}+\dfrac{1}{2}t\sqrt{t^2-4}-t\sqrt{t^2-4}+\log\dfrac{t+\sqrt{t^2-4}}{t-\sqrt{t^2-4}} \\
&= \dfrac{t^2}{2}-\dfrac{1}{2}t\sqrt{t^2-4}+\log\dfrac{\left(t+\sqrt{t^2-4}\right)^2}{4} \\
&= \dfrac{t\left(t-\sqrt{t^2-4}\right)}{2}+2\log\dfrac{t+\sqrt{t^2-4}}{2}
\end{align}$$となるので
$$\begin{eqnarray}
&& \displaystyle\lim_{t\to\infty}\big(S(t)-2\log t\big) \\
&=& \displaystyle\lim_{t\to\infty}\left\{\dfrac{4t}{2\left(t+\sqrt{t^2-4}\right)}+2\log\dfrac{t+\sqrt{t^2-4}}{2t}\right\} \\
&=& \displaystyle\lim_{t\to\infty}\left(\dfrac{2}{1+\sqrt{1-\dfrac{4}{t^2}}}+2\log\dfrac{1+\sqrt{1-\dfrac{4}{t^2}}}{2}\right) \\
&=& \dfrac{2}{1+1}+2\log\dfrac{1+1}{2} \\[0.3em]
&=& \mathbf{1}
\end{eqnarray}$$

解説

メインは積分計算・極限計算なので、領域の図示に関する説明はさらっと書いて大丈夫です。

積分自体は簡単ですが、代入する際に計算ミスしないよう注意しましょう。

分子の有理化や、最高次数で除すなど、極限の計算は基本的なものの組み合わせなので、しっかり確認しておきましょう。

まとめ

今回は、大阪大学理系数学（2020年 第4問）の解説をしました。