一橋大学 数学 2022年 第4問 解説

今回は、一橋大学数学（2022年 第4問）の解説をしたいと思います。

問題

　$t$ を実数とし，座標空間に点 $\mathrm{A}(t-1,\,t,\,t+1)$ をとる。また，$(0,\,0,\,0), \ $$(1,\,0,\,0), \ $$(0,\,1,\,0), \ $$(1,\,1,\,0), \ $$(0,\,0,\,1), \ $$(1,\,0,\,1), \ $$(0,\,1,\,1), \ $$(1,\,1,\,1)$ を頂点とする立方体を $D$ とする。点 $\mathrm{P}$ が $D$ の内部およびすべての面上を動くとき，線分 $\mathrm{AP}$ の動く範囲を $W$ とし，$W$ の体積を $f(t)$ とする。

⑴　$f(-1)$ を求めよ。

⑵　$f(t)$ のグラフを描き，$f(t)$ の最小値を求めよ。

（一橋大学）

解答

⑴

立方体 $D$ を構成する $6$ つの面について、平面 $x=0$，$x=1$，$y=0$，$y=1$，$z=0$，$z=1$ 上にあるものをそれぞれ $S_1,\,$$S_2,\,$$S_3,\,$$S_4,\,$$S_5,\,$$S_6$ とする。

$t=-1$ のとき $\mathrm{A}(-2,\,-1,\,0)$ である。

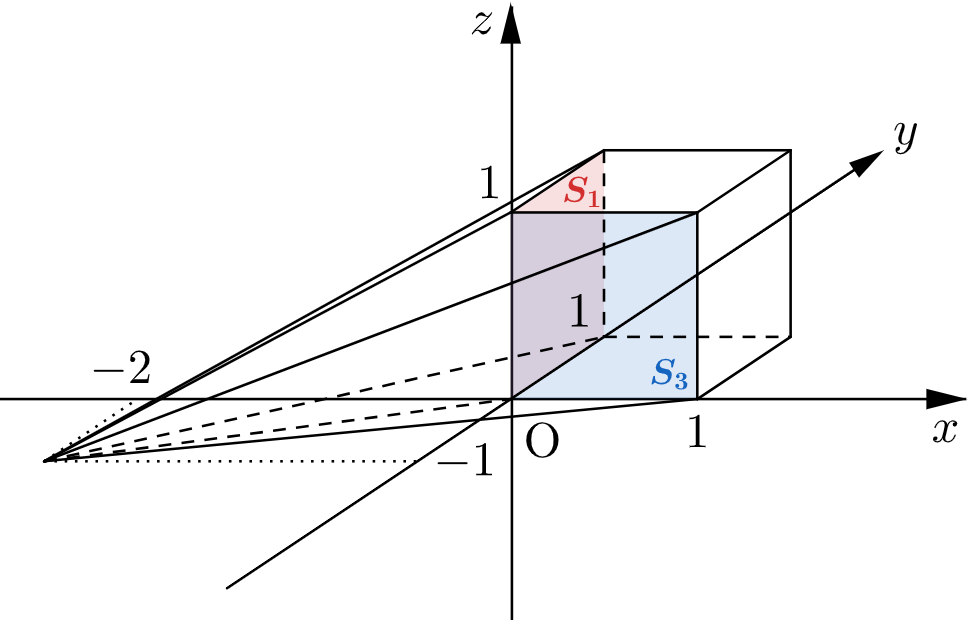
ここで、「頂点が $\mathrm{A}$ で底面が $S_n$ の四角錐」を $Q(S_n)$ と表す。

$t=-1$ のとき、$W$ は $D$ と $Q(S_1)$ と $Q(S_3)$ を合わせたものなので、その体積 $f(-1)$ は
$$f(-1)=1^3+\dfrac{1}{3}\cdot1\cdot1+\dfrac{1}{3}\cdot1\cdot2=\mathbf{2}$$

⑵

解法1（まとめて）

$W$ は $D,\,$$Q(S_1),\,$$Q(S_2),\,$$Q(S_3),\,$$Q(S_4),\,$$Q(S_5),\,$$Q(S_6)$ を合わせたものの半分なので
$$\begin{align}
f(t) &= \dfrac{1}{2}\cdot\left\{1^3+\dfrac{1}{3}\cdot1\cdot(|\,t-1\,|+|\,t-1-1\,|+|\,t\,|+|\,t-1\,|+|\,t+1\,|+|\,t+1-1\,|)\right\} \\
&= \dfrac{1}{6}(|\,t-2\,|+2|\,t-1\,|+2|\,t\,|+|\,t+1\,|)+\dfrac{1}{2}
\end{align}$$

(ⅰ)　$t\leqq-1$ のとき
$$\begin{align}
f(t) &= \dfrac{1}{6}(-t+2-2t+2-2t-t-1)+\dfrac{1}{2} \\
&= -t+1
\end{align}$$

(ⅱ)　$-1\lt t\leqq0$ のとき
$$\begin{align}
f(t) &= \dfrac{1}{6}(-t+2-2t+2-2t+t+1)+\dfrac{1}{2} \\
&= -\dfrac{2}{3}t+\dfrac{4}{3}
\end{align}$$

(ⅲ)　$0\lt t\leqq1$ のとき
$$\begin{align}
f(t) &= \dfrac{1}{6}(-t+2-2t+2+2t+t+1)+\dfrac{1}{2} \\
&= \dfrac{4}{3}
\end{align}$$

(ⅳ)　$1\lt t\leqq2$ のとき
$$\begin{align}
f(t) &= \dfrac{1}{6}(-t+2+2t-2+2t+t+1)+\dfrac{1}{2} \\
&= \dfrac{2}{3}t+\dfrac{2}{3}
\end{align}$$

(ⅴ)　$2\lt t$ のとき
$$\begin{align}
f(t) &= \dfrac{1}{6}(t-2+2t-2+2t+t+1)+\dfrac{1}{2} \\
&= t
\end{align}$$

(ⅰ)～(ⅴ)より、$f(t)$ のグラフは下図のようになる。

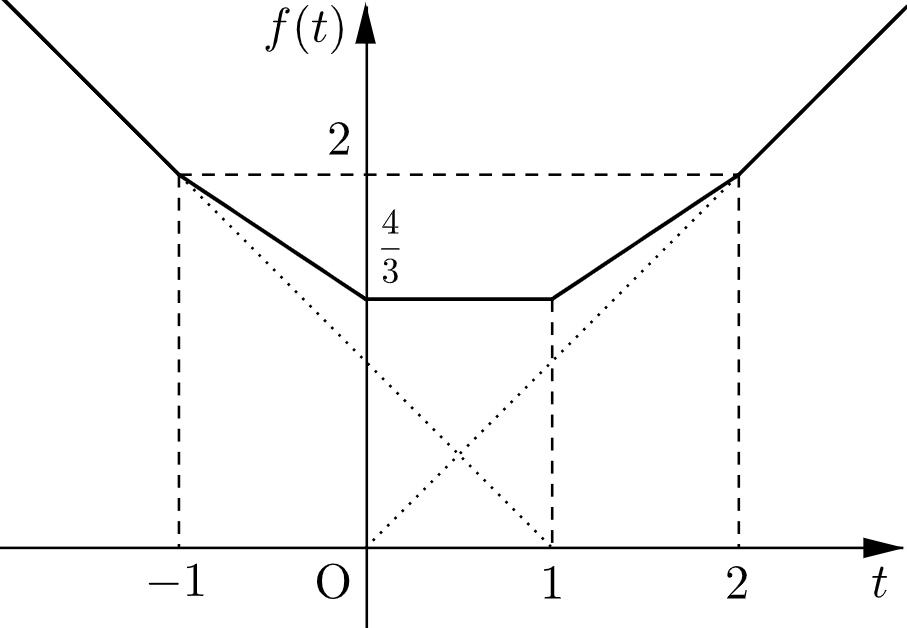
また、$f(t)$ の最小値は $\boldsymbol{\dfrac{4}{3}}$ である。

解法2（個別に）

座標空間の原点を $\mathrm{O}$ とすると
$$\overrightarrow{\mathrm{OA}}=(-1,\,0,\,1)+t(1,\,1,\,1)$$となるので、点 $\mathrm{A}$ は、点 $(-1,\,0,\,1)$ を通り $(1,\,1,\,1)$ を方向ベクトルとする直線上を動く。

この直線は $(-2,\,-1,\,0)$，$(-1,\,0,\,1)$ を通るので、$0\leqq z\leqq1$ において $0\leqq x\leqq1$，$0\leqq y\leqq1$ を満たす $D$ とは共有点をもたない。

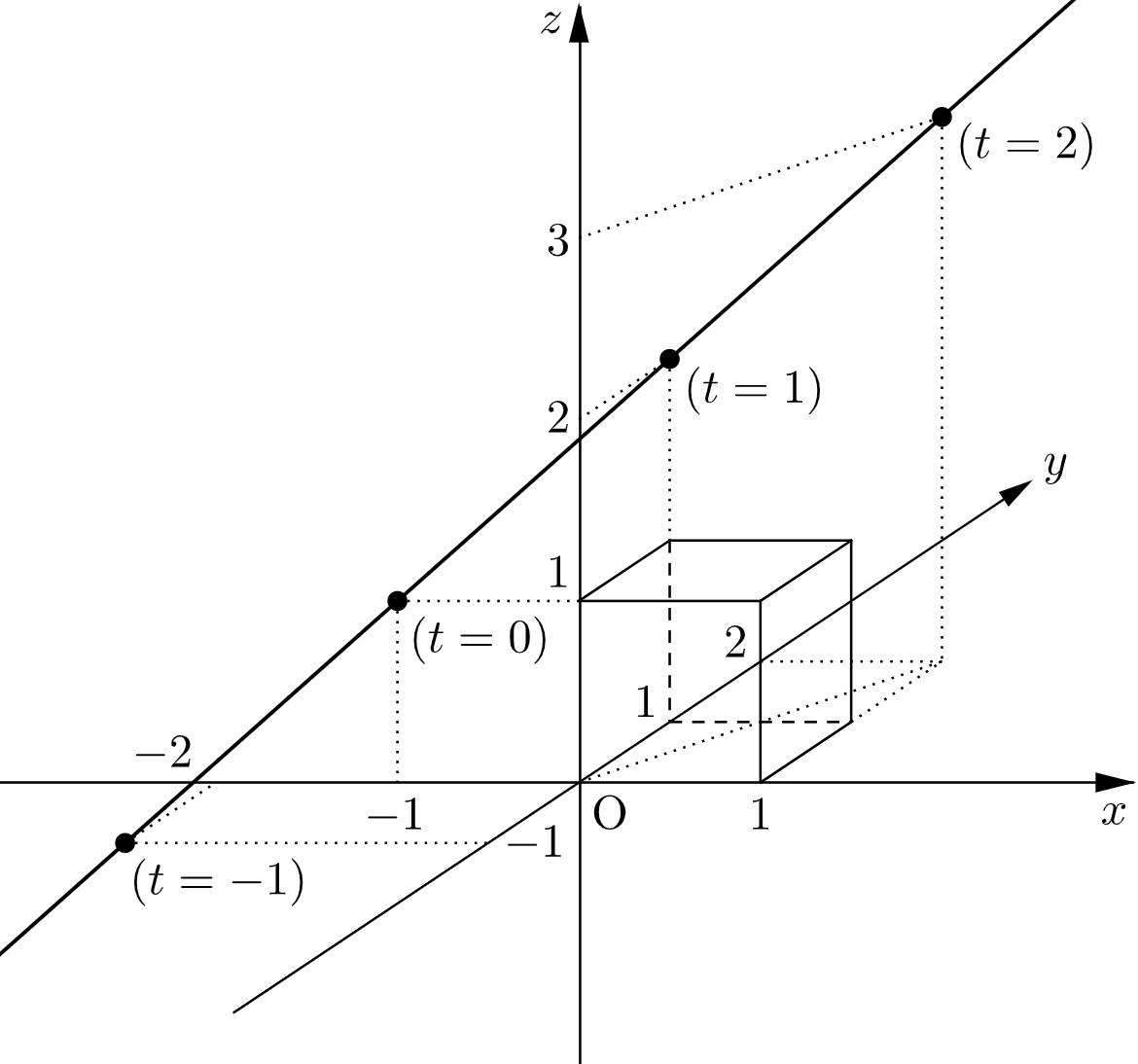
(ⅰ)　$t\leqq-1$ のとき
$W$ は $D$ と $Q(S_1)$ と $Q(S_3)$ と $Q(S_5)$ を合わせたものなので
$$\begin{align}
f(t) &= 1^3+\dfrac{1}{3}\cdot1\cdot(|\,t-1\,|+|\,t\,|+|\,t+1\,|) \\
&= 1+\dfrac{1}{3}\cdot(-t+1-t-t-1) \\[0.2em]
&= -t+1
\end{align}$$

(ⅱ)　$-1\lt t\leqq0$ のとき
$W$ は $D$ と $Q(S_1)$ と $Q(S_3)$ を合わせたものなので
$$\begin{align}
f(t) &= 1^3+\dfrac{1}{3}\cdot1\cdot(|\,t-1\,|+|\,t\,|) \\
&= 1+\dfrac{1}{3}\cdot(-t+1-t) \\
&= -\dfrac{2}{3}t+\dfrac{4}{3}
\end{align}$$

(ⅲ)　$0\lt t\leqq1$ のとき
$W$ は $D$ と $Q(S_1)$ と $Q(S_6)$ を合わせたものなので
$$\begin{align}
f(t) &= 1^3+\dfrac{1}{3}\cdot1\cdot(|\,t-1\,|+|\,t+1-1\,|) \\
&= 1+\dfrac{1}{3}\cdot(-t+1+t) \\
&= \dfrac{4}{3}
\end{align}$$

(ⅳ)　$1\lt t\leqq2$ のとき
$W$ は $D$ と $Q(S_4)$ と $Q(S_6)$ を合わせたものなので
$$\begin{align}
f(t) &= 1^3+\dfrac{1}{3}\cdot1\cdot(|\,t-1\,|+|\,t+1-1\,|) \\
&= 1+\dfrac{1}{3}\cdot(t-1+t) \\
&= \dfrac{2}{3}t+\dfrac{2}{3}
\end{align}$$

(ⅴ)　$2\lt t$ のとき
$W$ は $D$ と $Q(S_2)$ と $Q(S_4)$ と $Q(S_6)$ を合わせたものなので
$$\begin{align}
f(t) &= 1^3+\dfrac{1}{3}\cdot1\cdot(|\,t-1-1\,|+|\,t-1\,|+|\,t+1-1\,|) \\
&= 1+\dfrac{1}{3}\cdot(t-2+t-1+t) \\[0.2em]
&= t
\end{align}$$

(ⅰ)～(ⅴ)より、$f(t)$ のグラフは下図のようになる。

また、$f(t)$ の最小値は $\boldsymbol{\dfrac{4}{3}}$ である。

解説

$t$ の値によって立方体 $D$ と点 $\mathrm{A}$ の位置関係がどう変化するのかを問う、空間把握の力が必要な問題です。

⑴は、問題設定を具体的な値で把握するための問題です。$W$ が $D$ と $2$ つの四角錐を合わせたものだと気づくことがポイントです。

⑵は、解法2を想定した人が多いと思いますが、実は解法1のように、絶対値を使って $f(t)$ を $1$ つの式で表現することができます。

$D$ と $Q(S_1)\,$～$\,Q(S_6)$ をすべて足すと、$W \ 2$ 個分となります。空間図形なので簡単には分かりづらいですが、冷静に考えると確かにそうなっていることが分かります。

どちらの解法を選んだとしても場合分けが多く面倒くさいですが、$1$ つずつ丁寧に処理しましょう。

まとめ

今回は、一橋大学数学（2022年 第4問）の解説をしました。