今回は、一橋大学数学(2022年 第3問)の解説をしたいと思います。
問題
次の問いに答えよ。
⑴ 実数 $x,\,y$ について,「$\,|\,x-y\,|\leqq x+y\,$」であることの必要十分条件は「$\,x\geqq0$ かつ $y\geqq0\,$」であることを示せ。
⑵ 次の不等式で定まる $xy$ 平面上の領域を図示せよ。
(一橋大学)
$$|\,1+y-2x^2-y^2\,|\leqq1-y-y^2$$
解答
⑴
$$\begin{align}
&\hphantom{\Longleftrightarrow}\quad|\,x-y\,|\leqq x+y \\[0,3em]
&\Longleftrightarrow \ -(x+y)\leqq x-y\leqq x+y \\[0.3em]
&\Longleftrightarrow \
\left\{\begin{array}{l}
-(x+y)\leqq x-y \\
x-y\leqq x+y
\end{array}\right. \\[0.3em]
&\Longleftrightarrow \
\left\{\begin{array}{l}
0\leqq x \\
0\leqq y
\end{array}\right.
\end{align}$$より、題意は示された。$$\tag{証明終}$$
⑵
与式より
$$|\,(1-x^2-y^2)-(x^2-y)\,|\leqq(1-x^2-y^2)+(x^2-y)$$であり、これは⑴より
$$1-x^2-y^2\geqq0 \ \text{かつ} \ x^2-y\geqq0$$すなわち
$$x^2+y^2\leqq1 \ \text{かつ} \ y\leqq x^2$$と同値である。
円 $x^2+y^2=1$ と放物線 $y=x^2$ の共有点の $y$ 座標は、$y^2+y=1$ の解のうち $y\geqq0$ を満たすものなので $y=\dfrac{\sqrt{5}-1}{2}$ である。
よって、求める領域は、下図の網掛け部分である。ただし、境界を含む。
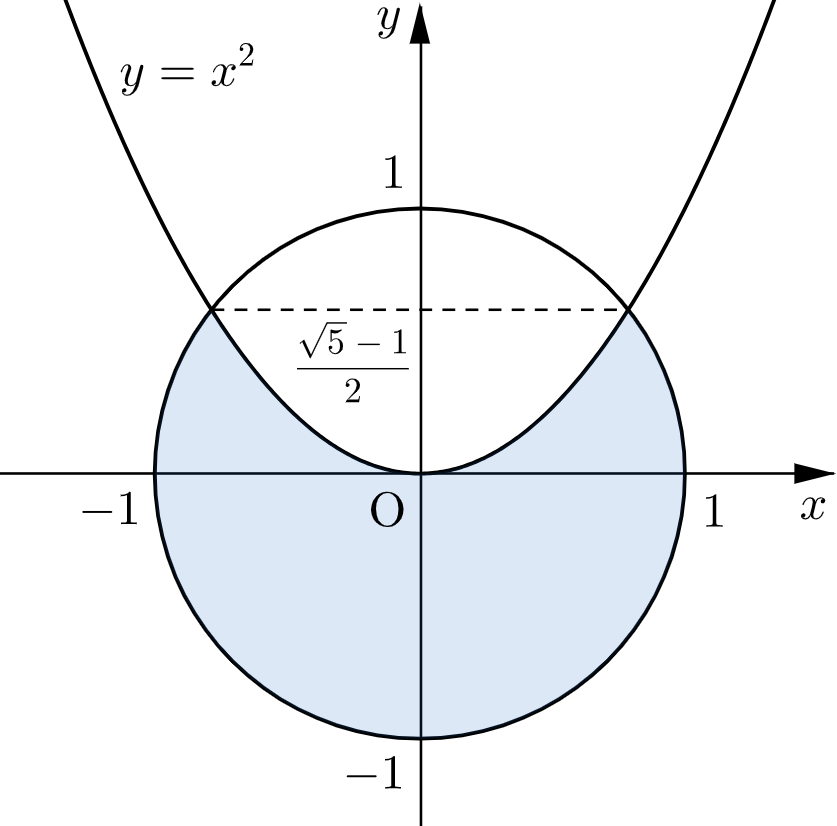
下図の網掛け部分(境界を含む)

解説
⑴は、絶対値の入った不等式の基本的な変形ができるかを問う問題です。文字が $2$ つありますが、$1$ 変数のときとすることは変わりません。
⑵は、⑴がなくても解けますが、本解答では⑴を利用した解き方としました。
まとめ
今回は、一橋大学数学(2022年 第3問)の解説をしました。
ほかの問題にもチャレンジしよう!
一橋大学 数学 2022年 第1問 解説
一橋大学 数学 2022年 第2問 解説
一橋大学 数学 2022年 第3問 解説
一橋大学 数学 2022年 第4問 解説
一橋大学 数学 2022年 第5問 解説













