東京大学 理系数学 2019年 第6問 解説

今回は、東京大学理系数学（2019年 第6問）の解説をしたいと思います。

問題

　複素数 $\alpha,\,\beta,\,\gamma,\,\delta$ および実数 $a,\,b$ が，次の $3$ 条件をみたしながら動く。

条件１：$\alpha,\,\beta,\,\gamma,\,\delta$ は相異なる。

条件２：$\alpha,\,\beta,\,\gamma,\,\delta$ は $4$ 次方程式 $z^4-2z^3-2az+b=0$ の解である。

条件３：複素数 $\alpha\beta+\gamma\delta$ の実部は $0$ であり，虚部は $0$ でない。

⑴　$\alpha,\,\beta,\,\gamma,\,\delta$ のうち，ちょうど $2$ つが実数であり，残りの $2$ つは互いに共役な複素数であることを示せ。

⑵　$b$ を $a$ で表せ。

⑶　複素数 $\alpha+\beta$ がとりうる範囲を複素数平面上に図示せよ。

（東京大学）

解答

⑴

$4$ 次方程式
$$z^4-2z^3-2az+b=0 \quad\cdots\text{①}$$の係数はすべて実数なので、その解は「すべて実数」「$\,2$ つの実数解と $2$ つの互いに共役な複素数」「$\,2$ 組の共役な複素数」のいずれかとなる。

(ⅰ)　①の解が「すべて実数」のとき

$\alpha\beta+\gamma\delta$ は実数となるので条件３に反する。

(ⅱ)　①の解が「$\,2$ 組の共役な複素数」のとき

①の解は、虚数 $w_1,\,$$w_2$ を用いて $z=w_1,\,\overline{w_1},\,w_2,\,\overline{w_2}$ と表せる。

対称性から $\alpha=w_1$ としても一般性を失わず、さらに $\beta=\overline{w_1}$ または $\gamma=\overline{w_1}$ のときを考えればよい。

・$\alpha=w_1$，$\beta=\overline{w_1}$ のとき
$$\alpha\beta+\gamma\delta=w_1\overline{w_1}+w_2\overline{w_2}=|\,w_1\,|^2+|\,w_2\,|^2$$より、$\alpha\beta+\gamma\delta$ は実数となるので条件３に反する。

・$\alpha=w_1$，$\gamma=\overline{w_1}$ のとき
対称性から $\beta=w_2$，$\delta=\overline{w_2}$ としてよく
$$\begin{align}
\overline{\alpha\beta+\gamma\delta} &= \overline{w_1w_2+\overline{w_1}\overline{w_2}} \\
&= \overline{w_1}\overline{w_2}+w_1w_2 \\
&= \alpha\beta+\gamma\delta
\end{align}$$より、$\alpha\beta+\gamma\delta$ は実数となるので条件３に反する。

(ⅰ),(ⅱ)より、$\alpha,\,\beta,\,\gamma,\,\delta$ のうち、ちょうど $2$ つが実数であり、残りの $2$ つは互いに共役な複素数である。$$\tag{証明終}$$

⑵

⑴より、実数 $k,\,$$\ell,\,$$p,\,$$q$ を用いて、①の解を $z=k,\,\ell,\,p+qi,\,p-qi$ と表せる。条件１より $k\ne\ell$，$q\ne0$ である。

条件２より、①の左辺は
$$z^4-2z^3-2az+b=(z-k)(z-\ell)\{z-(p+qi)\}\{z-(p-qi)\}$$と因数分解できる。

右辺を展開して、同じ次数の係数を比較すると
$$\left\{\begin{array}{l}
-(k+\ell+2p)=-2 \\
k\ell+2(k+\ell)p+p^2+q^2=0 \\
-\{2k\ell p+(k+\ell)(p^2+q^2)\}=-2a \\
k\ell(p^2+q^2)=b
\end{array}\right. \ \cdots\text{②}$$

$k,\,\ell,\,p+qi,\,p-qi$ と $\alpha,\,\beta,\,\gamma,\,\delta$ の対応として、対称性から次の(ⅰ),(ⅱ)が考えられる。

(ⅰ)　$\{\alpha,\,\beta\}=\{k,\,\ell\}$，$\{\gamma,\,\delta\}=\{p+qi,\,p-qi\}$
(ⅱ)　$\{\alpha,\,\beta\}=\{k,\,p+qi\}$，$\{\gamma,\,\delta\}=\{\ell,\,p-qi\}$

(ⅰ)のとき
$$\alpha\beta+\gamma\delta=k\ell+p^2+q^2$$より、虚部が $0$ となるので条件３に反する。

(ⅱ)のとき
$$\alpha\beta+\gamma\delta=(k+\ell)p+(k-\ell)qi$$より、$k\ne\ell$，$q\ne0$ に注意すると虚部は $0$ でない。よって実部が $0$，すなわち
$$(k+\ell)p=0 \ \Longleftrightarrow \ \ell=-k \ \text{または} \ p=0$$のとき条件３を満たす。

・$\ell=-k$ のとき
$$\begin{align}
\text{②} \ &\Longleftrightarrow \ \left\{\begin{array}{l}
p=1 \\
-k^2+p^2+q^2=0 \\
-k^2p=a \\
-k^2(p^2+q^2)=b
\end{array}\right. \\[0.3em]
&\Longleftrightarrow \ \left\{\begin{aligned}
p &= 1 \\
q &= \pm\sqrt{k^2-1} \\
a &= -k^2 \\
b &= -k^4
\end{aligned}\right. \ \cdots\text{③}
\end{align}$$より、$b=-a^2.$

・$p=0$ のとき
$$\begin{align}
\text{②} \ &\Longleftrightarrow \ \left\{\begin{array}{l}
k+\ell=2 \\
k\ell+q^2=0 \\
(k+\ell)q^2=2a \\
k\ell q^2=b
\end{array}\right. \\[0.3em]
&\Longleftrightarrow \ \left\{\begin{aligned}
\ell &= 2-k \\
q &= \pm\sqrt{k(k-2)} \\
a &= k(k-2) \\
b &= -k^2(k-2)^2
\end{aligned}\right. \ \cdots\text{④}
\end{align}$$より、$b=-a^2.$

以上より
$$b=\boldsymbol{-a^2}.$$

⑶

⑵の(ⅱ)について考える。

・$\ell=-k$ のとき

③より、$k\ne\ell$，$q\ne0$ に注意すると
$$|\,k\,|\gt1 \quad\cdots\text{⑤}$$の範囲の $k$ に対して実数 $p, \ $$q, \ $$a, \ $$b$ が定まる。

このとき
$$\begin{align}
\alpha+\beta &= k+p+qi \\
&= k+1\pm\sqrt{k^2-1}\,i
\end{align}$$となるので、実数 $X,\,Y$ を用いて $\alpha+\beta=X+Yi$ とおくと
$$X=k+1,\quad Y=\pm\sqrt{k^2-1}.$$$2$ 式から $k$ を消去すると
$$(X-1)^2-Y^2=1.$$また、⑤より $X\lt0, \ 2\lt X.$

・$p=0$ のとき

④より、$k\ne\ell$，$q\ne0$ に注意すると
$$k\lt0, \ 2\lt k \quad\cdots\text{⑥}$$の範囲の $k$ に対して実数 $\ell, \ $$q, \ $$a, \ $$b$ が定まる。

このとき
$$\begin{align}
\alpha+\beta &= k+p+qi \\
&= k\pm\sqrt{k(k-2)}\,i
\end{align}$$となるので、実数 $X,\,Y$ を用いて $\alpha+\beta=X+Yi$ とおくと
$$X=k,\quad Y=\pm\sqrt{k(k-2)}.$$$2$ 式から $k$ を消去すると
$$(X-1)^2-Y^2=1.$$また、⑥より $X\lt0, \ 2\lt X.$

以上より、どちらの場合でも、$\alpha+\beta$ がとりうる範囲は 双曲線 $(x-1)^2-y^2=1$ から $2$ 点 $(0,0),\,$$(2,0)$ を除いたものとなり、これを複素数平面上に図示すると下図のようになる。

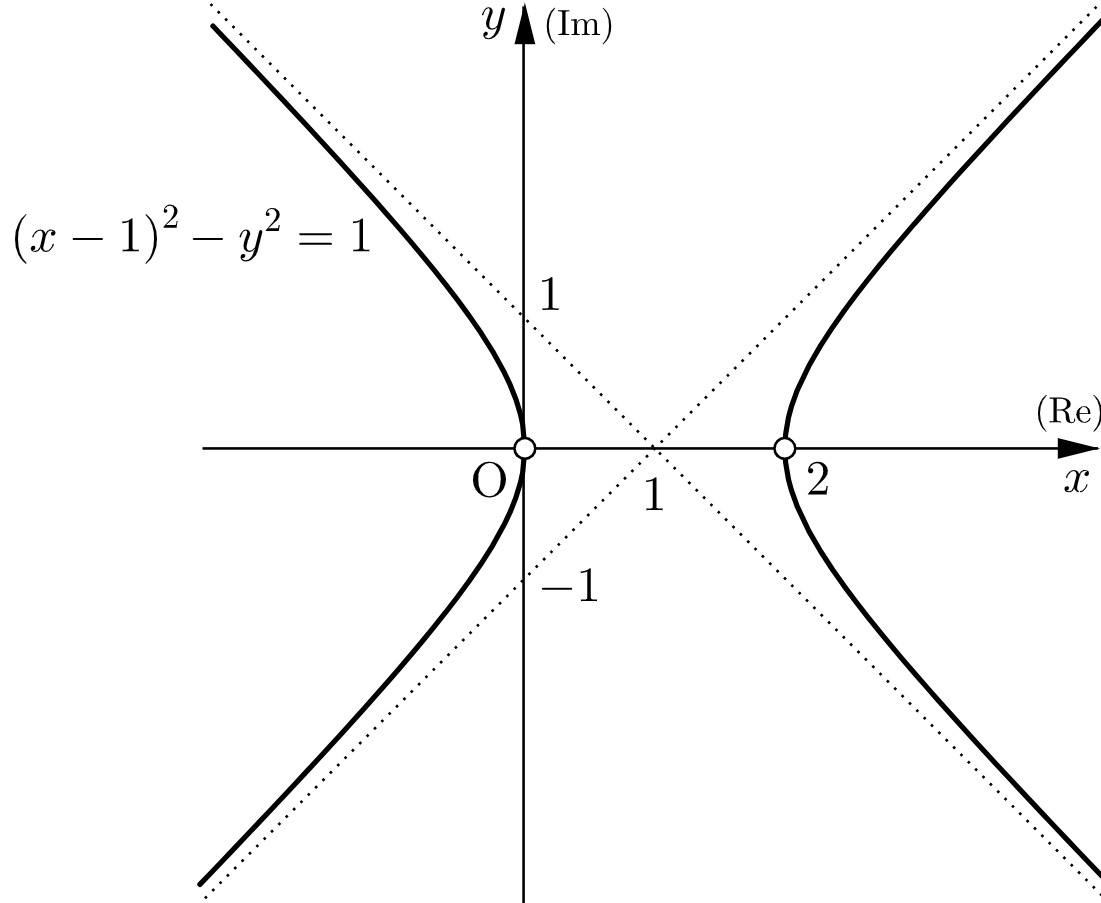
解説

⑴は、「実数係数多項式が虚数解をもつ場合、その共役な複素数も解となる」という性質を使いましょう。対称性と条件３を用いて、題意を示していきます。

⑵は、⑴で示したことを用いるために、実数を $4$ つ使って解を表します。$4$ つの解と $\alpha, \ $$\beta, \ $$\gamma, \ $$\delta$ の対応については、ここでも対称性からパターンを絞っていきます。

その後は、$4$ 次方程式バージョンの解と係数の関係（もちろん暗記しておくべきものではなく、その場で導きます。）を用いて、$b$ と $a$ の関係を導きます。
計算ミスが無ければ、立てた式から $b=-a^2$ は容易に分かります。

⑶は、⑵で使った連立方程式を用いて、$\alpha+\beta$ の軌跡を求める問題です。
軌跡上の点がすべて条件を満たすかきちんと吟味しましょう。

まとめ

今回は、東京大学理系数学（2019年 第6問）の解説をしました。