今回は、東京大学理系数学(2019年 第3問)の解説をしたいと思います。
問題
座標空間内に $5$ 点 $\mathrm{A}(2,\,0,\,0), \ $$\mathrm{B}(0,\,2,\,0), \ $$\mathrm{C}(-2,\,0,\,0), \ $$\mathrm{D}(0,\,-2,\,0), \ $$\mathrm{E}(0,\,0,\,-2)$ を考える。線分 $\mathrm{AB}$ の中点 $\mathrm{M}$ と線分 $\mathrm{AD}$ の中点 $\mathrm{N}$ を通り,直線 $\mathrm{AE}$ に平行な平面を $\alpha$ とする。さらに,$p$ は $2\lt p\lt4$ をみたす実数とし,点 $\mathrm{P}(p,\,0,\,2)$ を考える。
⑴ 八面体 $\mathrm{PABCDE}$ の平面 $y=0$ による切り口および,平面 $\alpha$ の平面 $y=0$ による切り口を同一平面上に図示せよ。
⑵ 八面体 $\mathrm{PABCDE}$ の平面 $\alpha$ による切り口が八角形となる $p$ の範囲を求めよ。
⑶ 実数 $p$ が⑵で定まる範囲にあるとする。八面体 $\mathrm{PABCDE}$ の平面 $\alpha$ による切り口のうち $y\geqq0$,$z\geqq0$ の部分を点 $(x,\,y,\,z)$ が動くとき,座標平面上で点 $(y,z)$ が動く範囲の面積を求めよ。
(東京大学)
解答
⑴
平面 $y=0$ による八面体 $\mathrm{PABCDE}$ と平面 $\alpha$ の切り口をそれぞれ $S,\,$$T$ とする。
$S$ は四角形 $\mathrm{PAEC}$ となる。
$T$ について考える。
$\mathrm{M}(1,\,1,\,0)$,$\mathrm{N}(1,\,-1,\,0)$ より、直線 $\mathrm{MN}$ と平面 $y=0$ の交点を $\mathrm{F}$ とすると、$\mathrm{F}(1,\,0,\,0)$ である。
直線 $\mathrm{AE}$ の式は
$$y=0,\quad z=x-2$$なので、$T$ は点 $\mathrm{F}$ を通り直線 $\mathrm{AE}$ に平行な直線、すなわち
$$y=0,\quad z=x-1 \quad\cdots\text{①}$$となる。
点 $\mathrm{P}$ が $T$ 上にあるとき
$$2=p-1 \ \Longleftrightarrow \ p=3.$$
したがって、$S,\,T$ を図示すると下図のようになる。
$2\lt p\lt 3$ のとき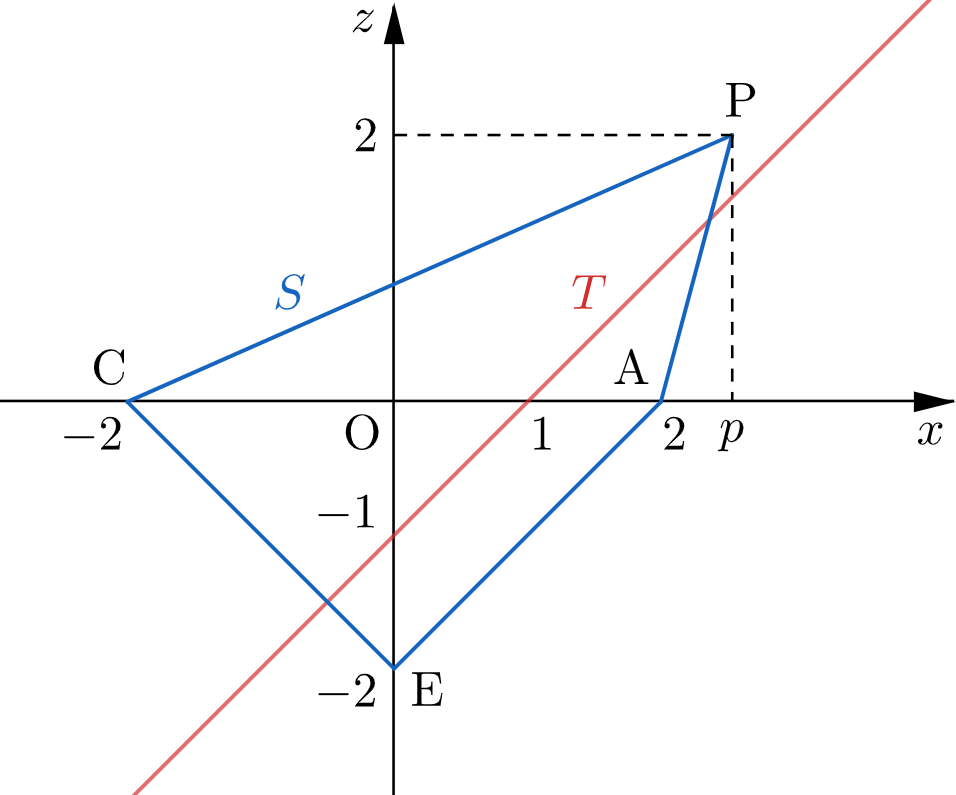
$p=3$ のとき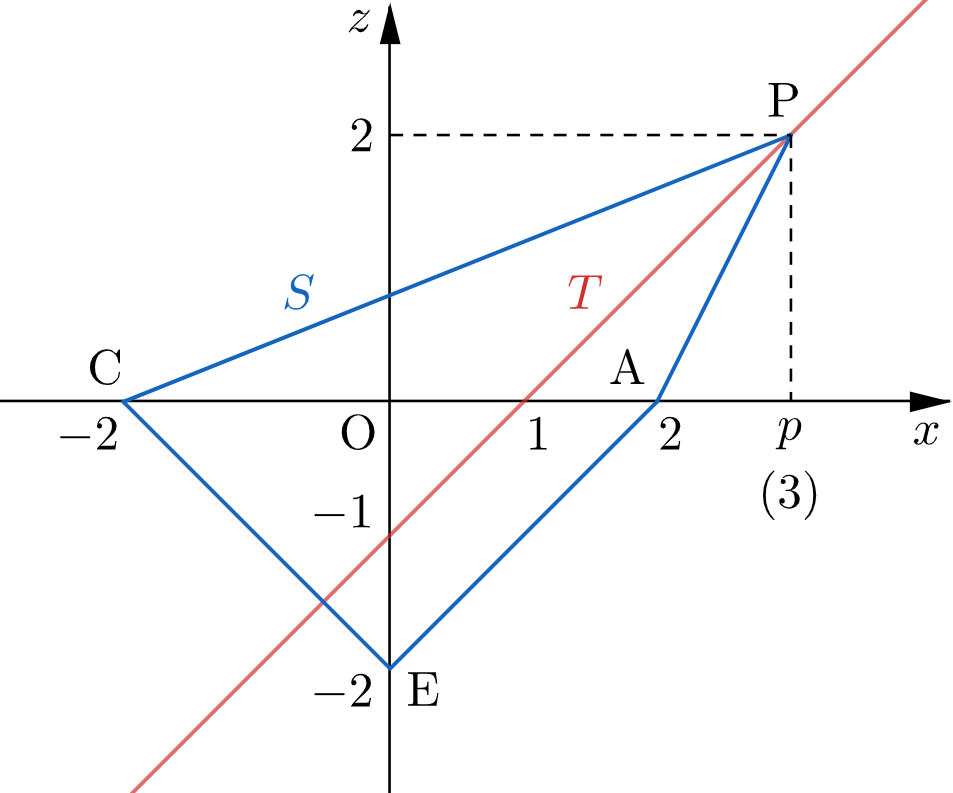
$3\lt p\lt 4$ のとき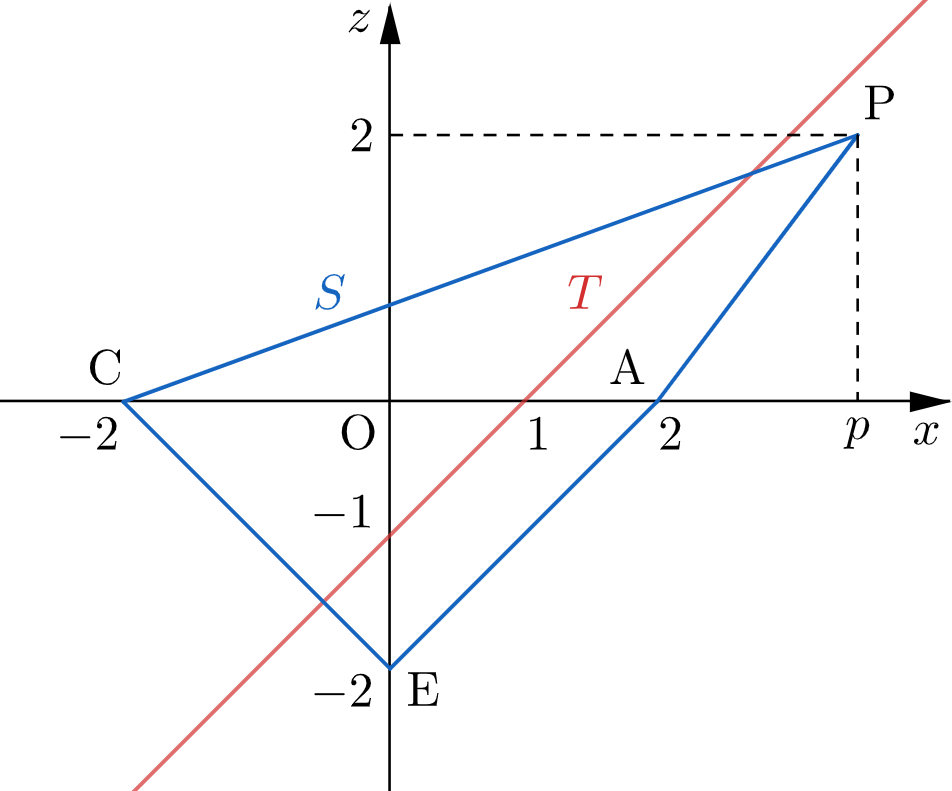
$2\lt p\lt 3$ のとき
$p=3$ のとき
$3\lt p\lt 4$ のとき
⑵
⑴より、$2\lt p\leqq3$ のとき、平面 $\alpha$ は八面体 $\mathrm{PABCDE}$ の辺 $\mathrm{AB}, \ $$\mathrm{AP}, \ $$\mathrm{AD}, \ $$\mathrm{ED}, \ $$\mathrm{EC}, \ $$\mathrm{EB}$ と交わるので、題意の切り口は六角形となる(下図参照)。
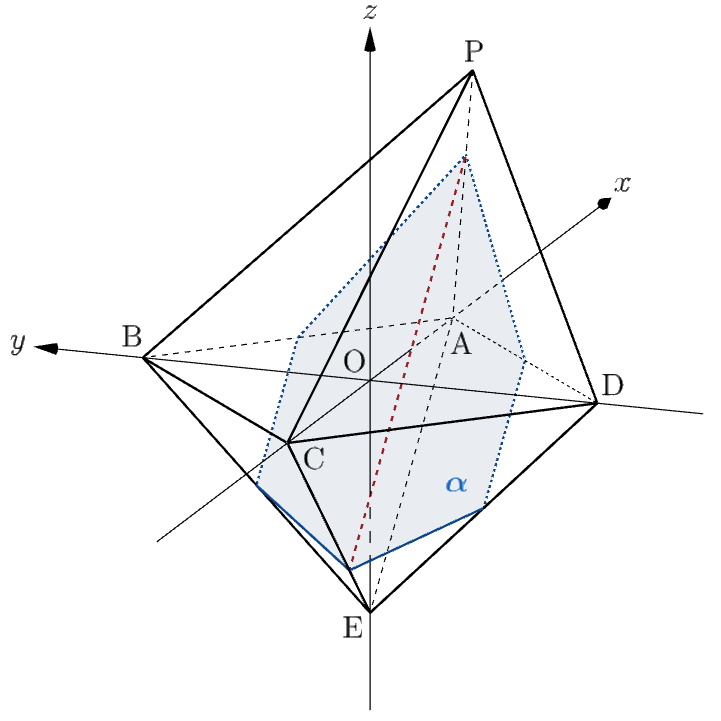
また、$3\lt p\lt4$ のとき、平面 $\alpha$ は八面体 $\mathrm{PABCDE}$ の辺 $\mathrm{AB}, \ $$\mathrm{PB}, \ $$\mathrm{PA}, \ $$\mathrm{PD}, \ $$\mathrm{AD}, \ $$\mathrm{ED}, \ $$\mathrm{EC}, \ $$\mathrm{EB}$ と交わるので、題意の切り口は八角形となる(下図参照)。
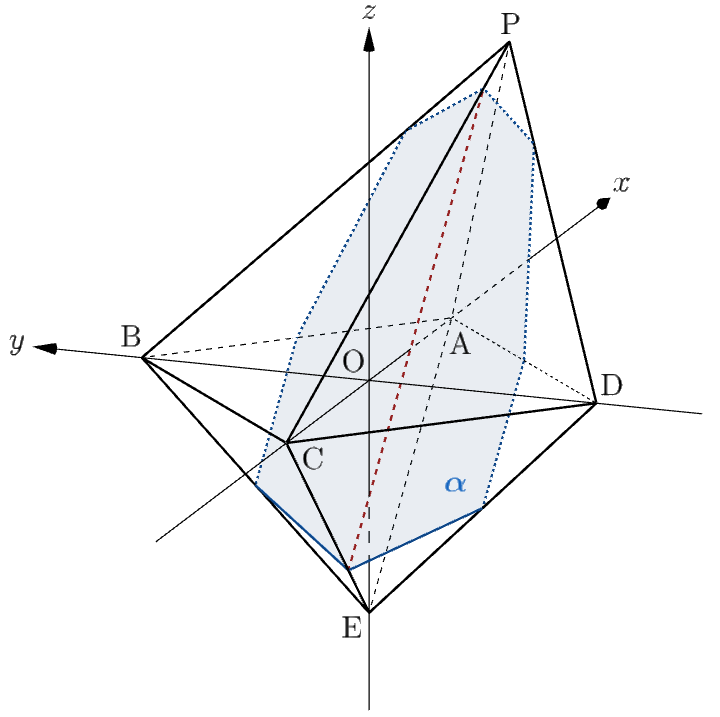
したがって、求める $p$ の範囲は
$$\boldsymbol{3\lt p\lt4}.$$
$$\boldsymbol{3\lt p\lt4}$$
⑶
$3\lt p\lt4$ のとき、$y\geqq0$,$z\geqq0$ における図は以下のようになる。
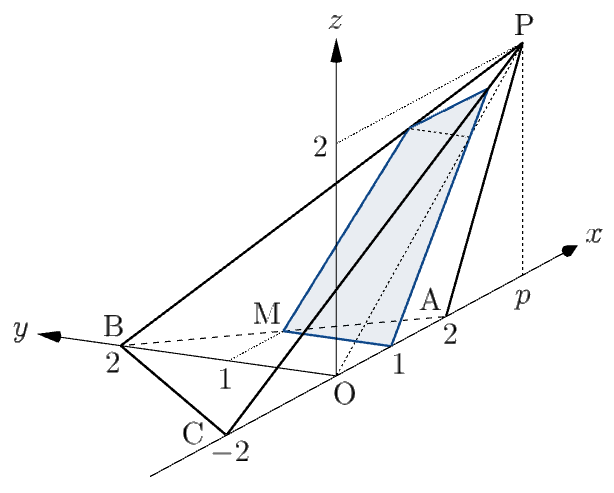
平面 $\alpha$ と辺 $\mathrm{AB}$ の交点は $\mathrm{M}(1,\,1,\,0)$ であり、平面 $\alpha$ と辺 $\mathrm{AC}$ の交点は $\mathrm{F}(1,\,0,\,0)$ である。
次に、平面 $\alpha$ と辺 $\mathrm{CP}$ の交点($\,\mathrm{G}$ とする。)の座標について考える。
平面 $y=0$ 上における直線 $\mathrm{CP}$ の方程式は
$$z=\dfrac{2}{p+2}(x+2)$$であり、これと①の交点が $\mathrm{G}$ なので、$\mathrm{G}$ の $x$ 座標は
$$\begin{align}
\dfrac{2}{p+2}(x+2) &= x-1 \\
2(x+2) &= (p+2)(x-1) \\[0.2em]
px &= p+6 \\[0.2em]
\therefore \ x &= \dfrac{p+6}{p}. \ \text{(}\because p\ne0\,\text{)}
\end{align}$$$\mathrm{G}$ は①上の点なので、$\mathrm{G}\left(\dfrac{p+6}{p},\,0,\,\dfrac{6}{p}\right)$ となる。
さらに、平面 $\alpha$ と辺 $\mathrm{BP}$ の交点($\,\mathrm{H}$ とする。)の座標について考える。
座標空間の原点を $\mathrm{O}$ とすると、平面 $y=0$ 上における直線 $\mathrm{OP}$ の方程式は
$$z=\dfrac{2}{p}x$$であり、これと①の交点の $x$ 座標は
$$\begin{align}
\dfrac{2}{p}x &= x-1 \\
2x &= px-p \\[0.2em]
\therefore \ x &= \dfrac{p}{p-2}. \ \text{(}\because p\ne2\,\text{)}
\end{align}$$
したがって、$\mathrm{H}$ は辺 $\mathrm{BP}$ を $\dfrac{p}{p-2}:\left(p-\dfrac{p}{p-2}\right)=1:(p-3)$ に内分する点である。よって、$\mathrm{H}\left(\dfrac{p}{p-2},\,\dfrac{2(p-3)}{p-2},\,\dfrac{2}{p-2}\right)$ となる。
以上より、八面体 $\mathrm{PABCDE}$ の平面 $\alpha$ による切り口のうち $y\geqq0$,$z\geqq0$ の部分は四角形 $\mathrm{FGHM}$ の周および内部であるから、この部分を点 $(x,\,y,\,z)$ が動くとき点 $(y,z)$ が動く範囲は、$4$ 点 $(0,\,0)$,$\left(0,\,\dfrac{6}{p}\right)$,$\left(\dfrac{2(p-3)}{p-2},\,\dfrac{2}{p-2}\right)$,$(1,\,0)$ を頂点とする四角形の周および内部である。
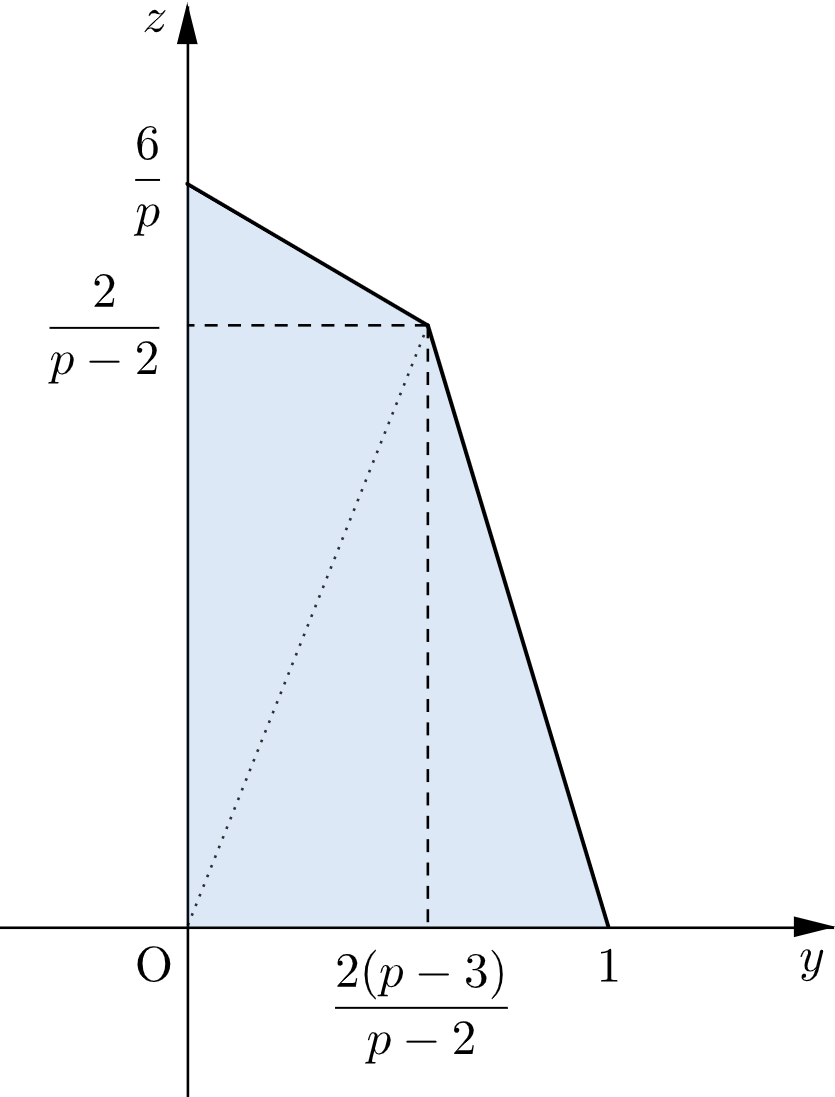
よって、求める面積は
$$\begin{align}
&\dfrac{1}{2}\cdot\dfrac{6}{p}\cdot\dfrac{2(p-3)}{p-2}+\dfrac{1}{2}\cdot1\cdot\dfrac{2}{p-2} \\[0.3em]
=\,\,&\boldsymbol{\dfrac{7p-18}{p(p-2)}}.
\end{align}$$
$$\boldsymbol{\dfrac{7p-18}{p(p-2)}}$$
解説
平面による八面体の切り口を考える、高い空間把握能力を必要とする問題です。
⑴は、八面体については、平面 $y=0$ 上にある頂点が $\mathrm{P},\,$$\mathrm{A},\,$$\mathrm{E},\,$$\mathrm{C}$ なので、切り口はこれらを結んでできる四角形だと分かります。
また平面 $\alpha$ については、直線 $\mathrm{MN}$ が $y$ 軸と平行かつ直線 $\mathrm{AE}$ が $y$ 軸と垂直なので、線分 $\mathrm{MN}$ の中点(解答では $\mathrm{F}\,$)を平行移動させた軌跡だと分かります。
⑵は、答えを出すだけならそこまで難しくはないですが、きちんと記述をしようとすると案外悩みます。
八角形になることを示すには、頂点が $8$ 個できることを示せばよいので、本解答では⑴の答えの図から $3$ 次元的にイメージして、$\alpha$ がどの辺と交わるかを列挙しました。
下のアニメーションを見ると、確かに $p=3$ を境目として六角形 $\leftrightarrow$ 八角形と切り口が変化していることが分かりますね。
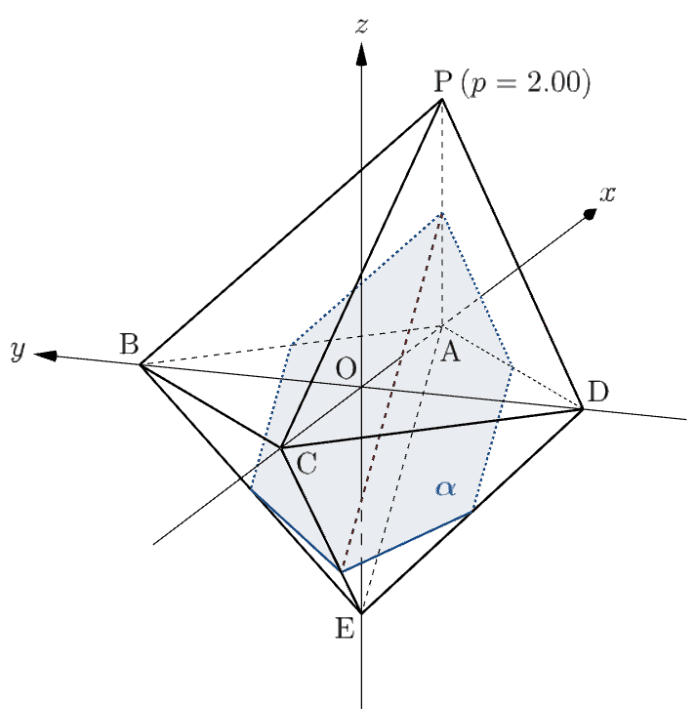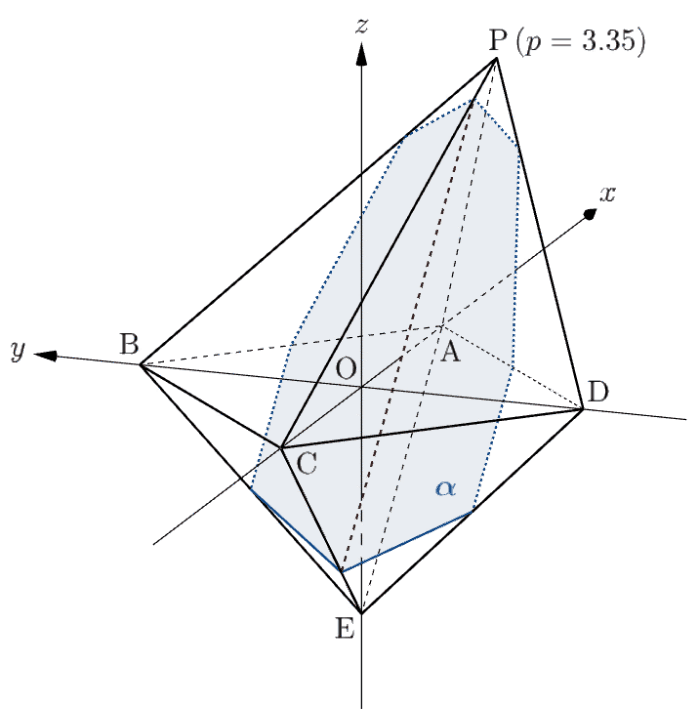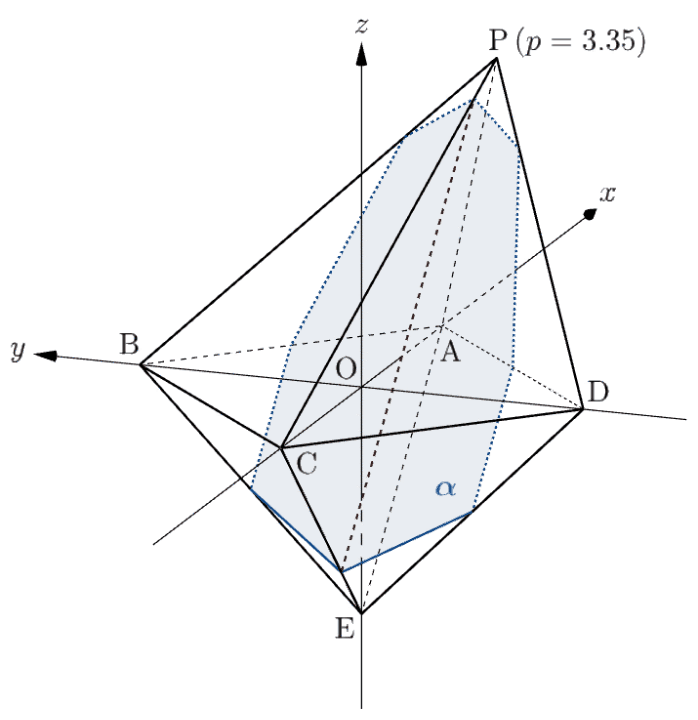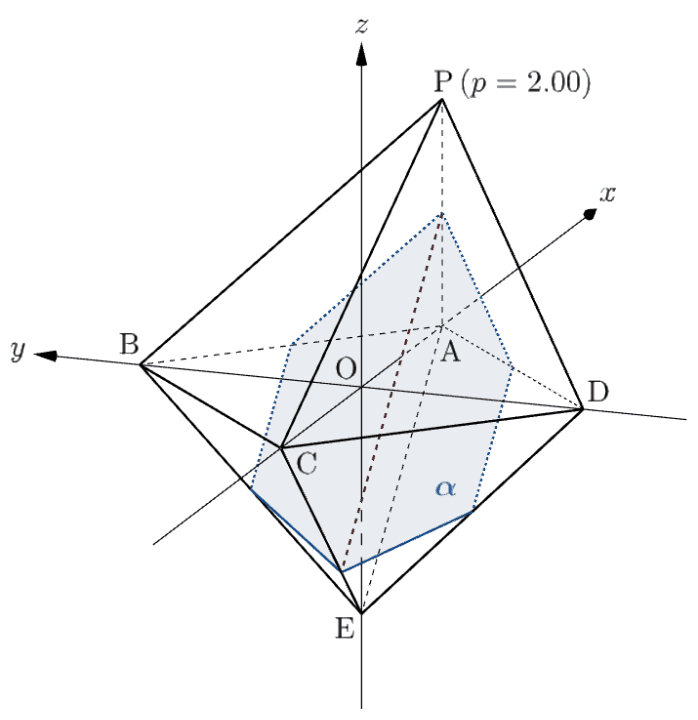
⑶は、題意の把握からややこしいです。要は、切り口の $y\geqq0$,$z\geqq0$ の部分を $yz$ 平面に投影するとどうなるかを問うています。
面積計算自体は簡単なので、四角形の $4$ 頂点の座標を求めるところが山場と言えるでしょう。
まとめ
今回は、東京大学理系数学(2019年 第3問)の解説をしました。
ほかの問題にもチャレンジしよう!
東京大学 理系数学 2019年 第1問 解説
東京大学 理系数学 2019年 第2問 解説
東京大学 理系数学 2019年 第3問 解説
東京大学 理系数学 2019年 第4問 解説
東京大学 理系数学 2019年 第5問 解説
東京大学 理系数学 2019年 第6問 解説













