京都大学 理学部特色入試（数学）2022年度 第4問 解説

今回は、京都大学理学部特色入試・数学（2022年度 第4問）の解説をしたいと思います。

問題

　$0$ 以上 $1$ 未満の実数 $p$ を固定する．$n$ を正の整数とし，$xy$ 平面上の領域 $D_n$ を $x+y\leqq n$ で定める．$xy$ 平面上の点 $P_0(0,n)$ から始まる点列 $P_0,P_1,P_2,\dots$ を以下の条件を満たすように定める．
　$(\mathrm{A})$　$P_k(x_k,y_k)$ が $y_k\gt 0$ を満たすならば，
　　(ⅰ)　確率 $p$ で $P_{k+1}$ を $(x_k+1,y_k)$ とおく．
　　(ⅱ)　確率 $1-p$ で $P_{k+1}$ を $(x_k,y_k-1)$ とおく．
　$(\mathrm{B})$　$P_k(x_k,y_k)$ が $y_k=0$ を満たすならば，$P_{k+1}$ を $P_k$ とおく．

このとき，以下の設問に答えよ．

⑴　$p=\dfrac{1}{2}$ のとき，$P_{n+k}$ が $(k,0)$ となる確率を $p_{n,k}$ とする．このとき
$$\displaystyle\sum_{k=0}^{\infty} kp_{n,k}$$を求めよ．

⑵　各々の $n$ に対し，上の操作で実現可能な点列 $P_0(0,n),P_1,P_2,\dots,P_{2n}$ で，これらすべての点が $D_n$ に属するものの総数を $C_n$ とする．また，$C_0=1$ とする．このとき，
$$C_{n+1} = \displaystyle\sum_{k=0}^{n} C_kC_{n-k}$$が成り立つことを示せ．

⑶　点列 $P_0(0,n),P_1,P_2,P_3,\dots$ のすべての点が領域 $D_n$ に属する確率を $q_n$ とする．このとき，
$$\displaystyle\lim_{n\to\infty} q_n$$を $p$ を用いて表せ．

ただし，正の実数の列 $\{a_j\}$ が，任意の正の整数 $m$ に対して $\displaystyle\sum_{j=1}^{m} a_j \leqq 1$ を満たすとき，以下が成り立つことを用いてもよい．
　・極限 $\displaystyle\lim_{m\to\infty} \displaystyle\sum_{j=1}^{m} a_j$ が存在する．この極限値を $a$ とすると $a\leqq 1.$
　・$a$ の値は実数の列 $\{a_j\}$ の順番を入れ替えたとしても変わらない．

（京都大学）

※ 問題訂正を反映させたものを掲載しています。

解答

⑴

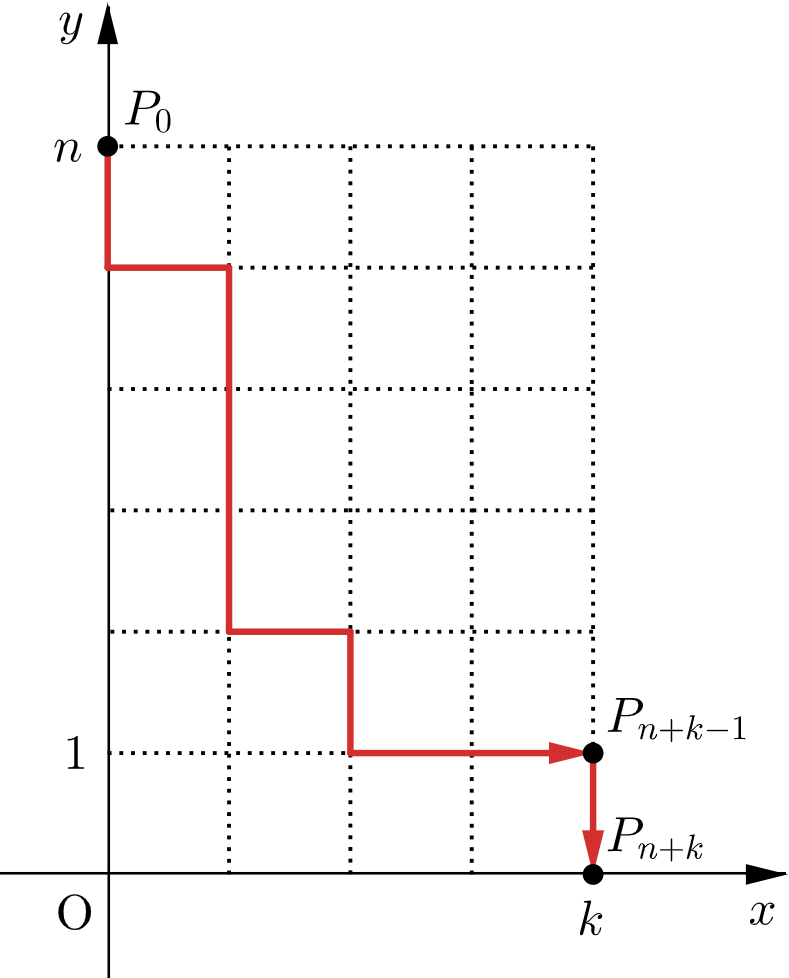
$P_{n+k}$ が $(k,0)$ となるのは、$P_{n+k-1}$ が $(k,1)$ となり、かつ確率 $\dfrac{1}{2}$ で $P_{n+k}(k,0)$ となるときである。$P_0(0,n)$ から $P_{n+k-1}(k,1)$ までの $(n+k-1)$ 回の移動のうち、$x$ 軸方向に $1$ だけ移動する回数は $k$ 回であるから、確率 $p_{n,k}$ は
$$\begin{align}
p_{n,k} &= {}_{n+k-1}\mathrm{C}_{k}\left(\dfrac{1}{2}\right)^{n+k-1}\cdot\dfrac{1}{2} \\
&= {}_{n+k-1}\mathrm{C}_{k} \cdot \dfrac{1}{2^{n+k}}
\end{align}$$となる。よって、$k\geqq 1$ のとき
$$\begin{align}
kp_{n,k} &= k \cdot {}_{n+k-1}\mathrm{C}_{k} \cdot \dfrac{1}{2^{n+k}} \\
&= k \cdot \dfrac{(n+k-1)!}{(n-1)!k!} \cdot \dfrac{1}{2^{n+k}} \\
&= n \cdot \dfrac{(n+k-1)!}{n!(k-1)!} \cdot \dfrac{1}{2^{n+k}} \\
&= n \cdot {}_{n+k-1}\mathrm{C}_{k-1} \cdot \dfrac{1}{2^{n+k}} \\
&= np_{n+1,k-1}
\end{align}$$となるので、$N$ を正の整数とすると
$$\begin{align}
\displaystyle\sum_{k=0}^{N} kp_{n,k} &= \displaystyle\sum_{k=1}^{N} kp_{n,k} \\
&= \displaystyle\sum_{k=1}^{N} np_{n+1,k-1} \\
&= n\displaystyle\sum_{k=0}^{N-1} p_{n+1,k}
\end{align}$$が成り立つ。

ここで、$0\leqq M \leqq N-2$ を満たす整数 $M$ に対して $P_{n+1+M}$ の $y$ 座標が $0$ ならば、条件 $(\mathrm{B})$ より $P_{n+N}$ の $y$ 座標も $0$ となるので、$\displaystyle\sum_{k=0}^{N-1} p_{n+1,k}$ は、$P_0(0,n+1)$ を初期位置として点の操作を $(n+N)$ 回行った結果、$P_{n+N}$ の $y$ 座標が $0$ となる確率を表している。

すなわち、$1-\displaystyle\sum_{k=0}^{N-1} p_{n+1,k}$ は、$P_0(0,n+1)$ を初期位置として点の操作を $(n+N)$ 回行った結果、$P_{n+N}$ の $y$ 座標が正となる確率を表している。

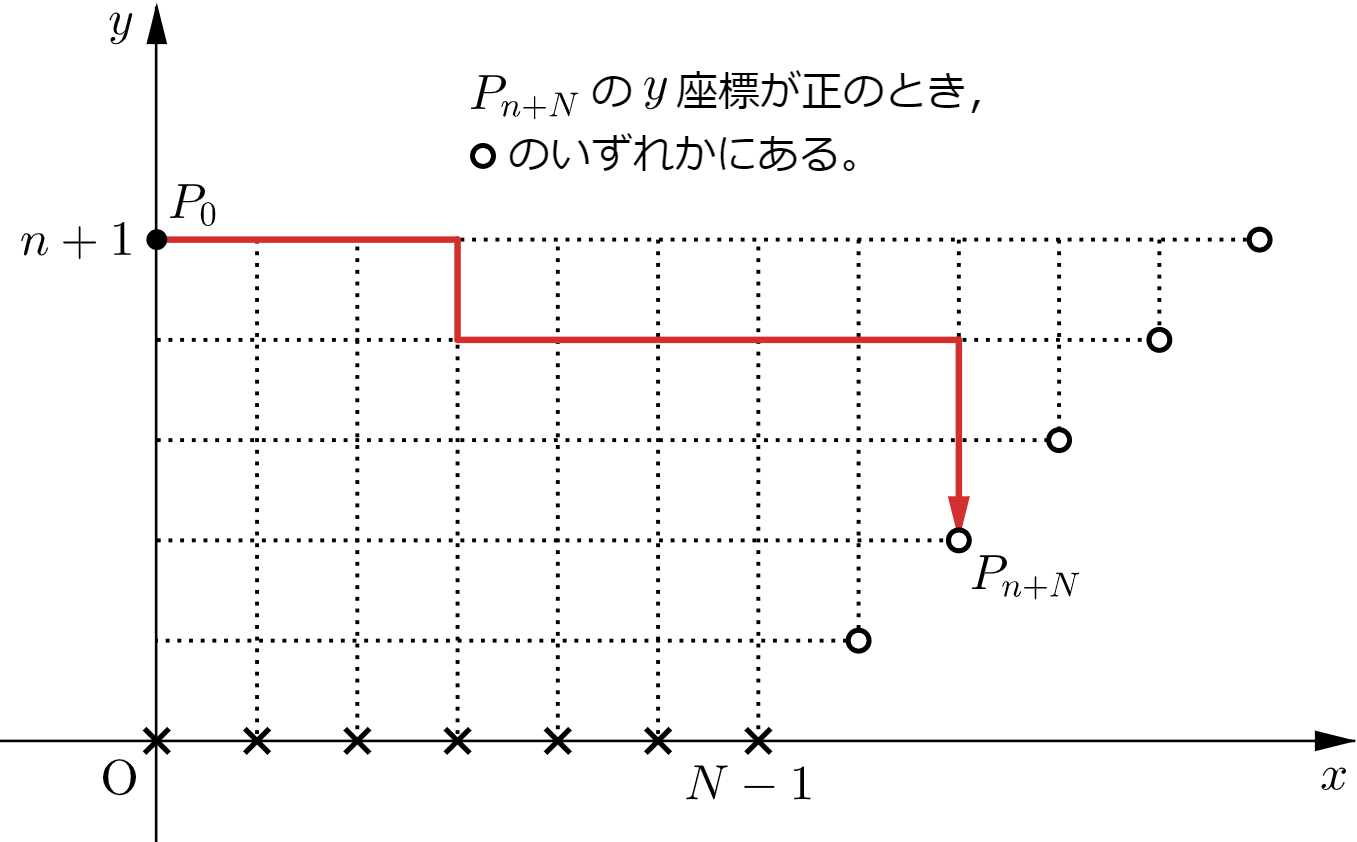
このとき、$(n+N)$ 回の点の移動のうち、$y$ 軸方向に $-1$ だけ移動する回数は $0,1,2,\cdots,n$ 回のいずれかであるから
$$\begin{align}
0 &\leqq 1-\displaystyle\sum_{k=0}^{N-1} p_{n+1,k} \\
&= \displaystyle\sum_{i=0}^{n} {}_{n+N}\mathrm{C}_{i} \cdot \left(\dfrac{1}{2}\right)^{n+N} \\
&= \dfrac{1}{2^{n+N}} \left( 1+ \displaystyle\sum_{i=1}^{n} {}_{n+N}\mathrm{C}_{i} \right) \\
&= \dfrac{1}{2^{n+N}} \left( 1+ \displaystyle\sum_{i=1}^{n} \displaystyle\prod_{j=0}^{i-1} \dfrac{n+N-j}{i-j} \right) \\
&\leqq \dfrac{1}{2^{n+N}} \left\{ N(n+N)^n+ \displaystyle\sum_{i=1}^{n} \displaystyle\prod_{j=0}^{i-1} (n+N) \right\} \\
&= \dfrac{1}{2^{n+N}} \left\{ N(n+N)^n+ \displaystyle\sum_{i=1}^{n} (n+N)^i \right\} \\
&\leqq \dfrac{1}{2^{n+N}} \left\{ N(n+N)^n+ n(n+N)^n \right\} \\
&= \dfrac{(n+N)^{n+1}}{2^{n+N}}
\end{align}$$となる。

$$\displaystyle \lim_{N\to\infty} \dfrac{(n+N)^{n+1}}{2^{n+N}} = 0 $$なので（補足1）、はさみうちの原理により
$$\displaystyle \lim_{N\to\infty} \displaystyle\sum_{k=0}^{N-1} p_{n+1,k} = 1$$となる。

よって
$$\begin{align}
\displaystyle\sum_{k=0}^{\infty} kp_{n,k}
&= \displaystyle \lim_{N\to\infty} \displaystyle\sum_{k=0}^{N} kp_{n,k} \\
&= n \displaystyle \lim_{N\to\infty} \displaystyle\sum_{k=0}^{N-1} p_{n+1,k} \\
&= \boldsymbol{n}
\end{align}$$

⑵

点列 $P_0(0,n+1),P_1,P_2,\cdots,P_{2n+2}$ で、これらすべての点が $D_{n+1}$ に属するものの総数 $C_{n+1}$ について考える。このとき、$P_1$ は $(0,n)$ となる。

ここで、$k$ を $1 \leqq k \leqq n-1$ を満たす整数とし、$P_0(0,n+1)$ から点を移動させる中で、最初に直線 $x+y=n+1$ 上に定まった点（ただし $P_0$ を除く。）の $y$ 座標を $n-k$ とする。この点は $P_{2k+2}(k+1,n-k)$ であるから、$P_{2k+1}(k,n-k)$ となる。

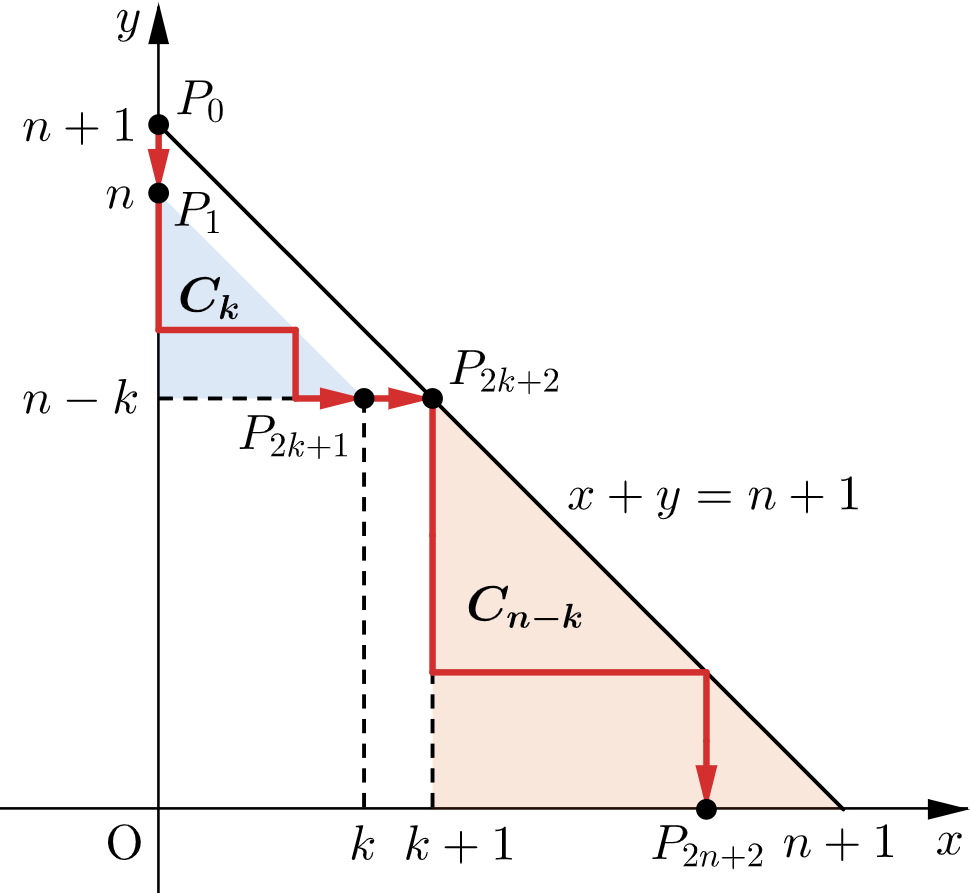
このとき、点列 $P_1,P_2,\cdots,P_{2k+1}$ の総数は $C_{k}$ 通りであり、点列 $P_{2k+2},P_{2k+3},\cdots,P_{2n+2}$ の総数は $C_{n-k}$ 通りである。

また、$P_2$ が $(1,n)$ となるときの点列 $P_0,P_1,P_2,\cdots,P_{2n+2}$ の総数は $C_n$ 通りである。

さらに、点列 $P_1,P_2,\cdots,P_{2n+2}$ のすべての点が直線 $x+y=n+1$ 上に定まらないとき、点列 $P_0,P_1,P_2,\cdots,P_{2n+2}$ の選び方は $C_{n}$ 通りである。

したがって、$C_0 = 1$ とすれば
$$\begin{align}
C_{n+1} &= \displaystyle\sum_{k=1}^{n-1} C_kC_{n-k} + 2C_n \\
&= \displaystyle\sum_{k=0}^{n} C_kC_{n-k}
\end{align}$$が成り立つ。$$\tag{証明終}$$

⑶

$p=0$ のとき、点は $y$ 軸方向に $-1$ ずつ移動するので、点列 $P_0(0,n),P_1,P_2,P_3,\dots$ のすべての点は領域 $D_n$ に属する。よって
$$\displaystyle\lim_{n\to\infty} q_n = 1$$である。

以下、$p=0$ とする。

$(0,n+1)$ を初期位置とする点列 $P_0(0,n+1),P_1,P_2,\cdots$ のいずれかが領域 $D_{n+1}$ に属さない確率 $1-q_{n+1}$ について考える。

ここで、$j$ を $0 \leqq j \leqq n$ を満たす整数とし、$P_0(0,n+1)$ から点を移動させる中で、最初に領域 $D_{n+1}$ に属さなくなった点の $y$ 座標を $n+1-j$ とする。

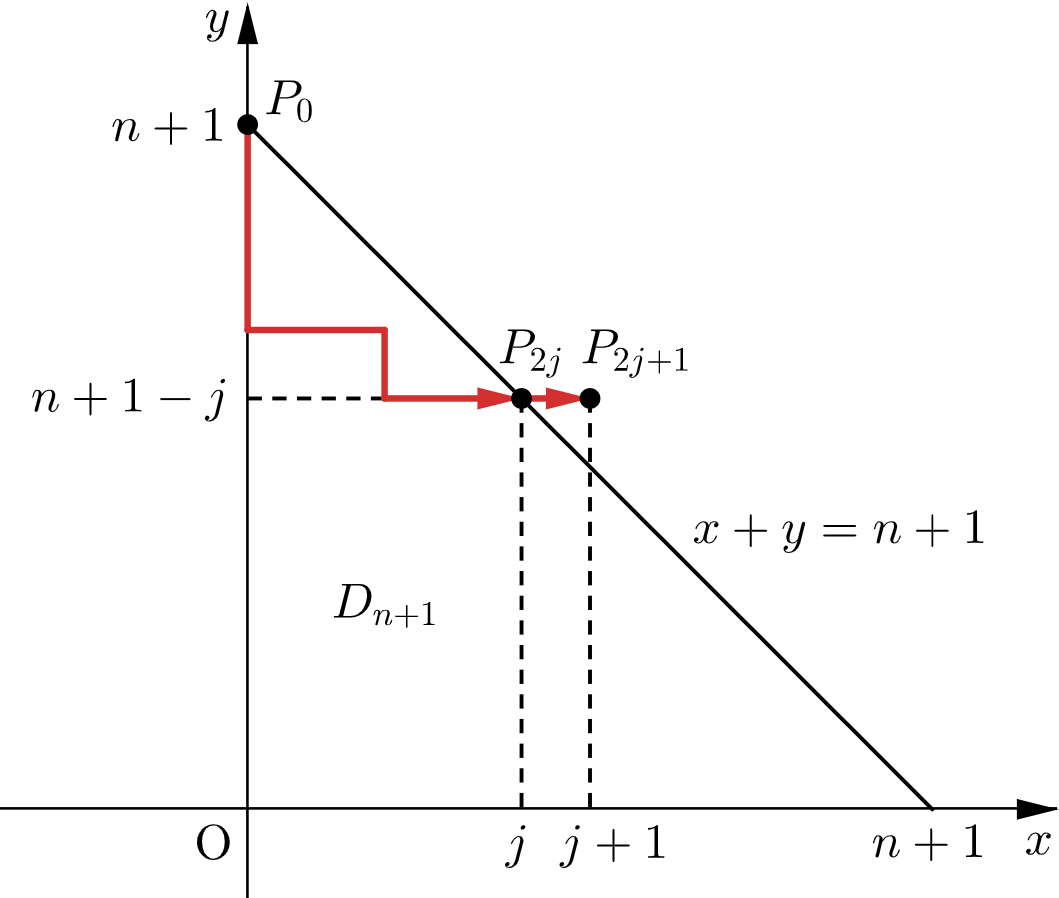
このとき、点列 $P_0,P_1,P_2,\cdots,P_{2j}(j,n+1-j)$ はすべて領域 $D_{n+1}$ に属し、$P_{2j+1}(j+1,n+1-j)$ が領域 $D_{n+1}$ に属さない状況となる。

このような点列 $P_0,P_1,P_2,\cdots,P_{2j+1}$ の総数は $C_{j}$ 通りであるから、確率 $1-q_{n+1}$ は
$$\displaystyle\sum_{j=0}^{n} C_{j} \cdot p^j (1-p)^j \cdot p \quad\cdots\text{①}$$となる。①は任意の正の整数 $n$ に対して $1$ 以下であるから、極限 $\displaystyle\lim_{n\to\infty} \displaystyle\sum_{j=0}^{n} C_{j} \cdot p^j (1-p)^j \cdot p$ が存在し、この極限値を $a_p$（ $\leqq 1$ ）とする。また、①で和をとる際に足す順番を入れ替えたとしても、$a_p$ の値は変わらない。

ここで、①において $p$ を $1-p$ と置き換えたものに対して
$$\begin{align}
a_{1-p} &= \displaystyle\lim_{n\to\infty} \displaystyle\sum_{j=0}^{n} C_{j} \cdot (1-p)^j p^j \cdot (1-p) \\
&= \dfrac{1-p}{p} \displaystyle\lim_{n\to\infty} \displaystyle\sum_{j=0}^{n} C_{j} \cdot p^j (1-p)^j \cdot p \\
&= \dfrac{1-p}{p}a_p \\[0.3em]
\therefore \ a_p &= \dfrac{p}{1-p}a_{1-p} \quad\cdots\text{②}
\end{align}$$が成り立つ。

以下、$a_p$ を単に $a$ と表す。

①の $C_j$ に⑵で示した結果を代入すると
$$\begin{eqnarray}
&& 1-q_{n+1} \\
&=& \displaystyle\sum_{j=0}^{n} C_{j} \cdot p^j (1-p)^j \cdot p \\
&=& p+p\displaystyle\sum_{j=1}^{n} C_{j} \cdot p^j (1-p)^j \\
&=& p+p\displaystyle\sum_{j=1}^{n} \left\{ p^j (1-p)^j \displaystyle\sum_{k=0}^{j-1} C_kC_{j-k-1} \right\} \\
&=& p+p\displaystyle\sum_{j=0}^{n-1} \left\{ p^{j+1} (1-p)^{j+1} \displaystyle\sum_{k=0}^{j} C_kC_{j-k} \right\} \\
&=& p+p^2(1-p) \displaystyle\sum_{j=0}^{n-1} \displaystyle\sum_{k=0}^{j} C_kC_{j-k} \cdot p^j (1-p)^j \quad\cdots\text{③}
\end{eqnarray}$$ここで、$0\leqq j \leqq n-1$ の各 $j$ に対して $k=0,1,\cdots,j$ を代入したものの総和は、$0\leqq k \leqq n-1$ の各 $k$ に対して $j=k,k+1,\cdots,n-1$ を代入したものの総和に等しい。

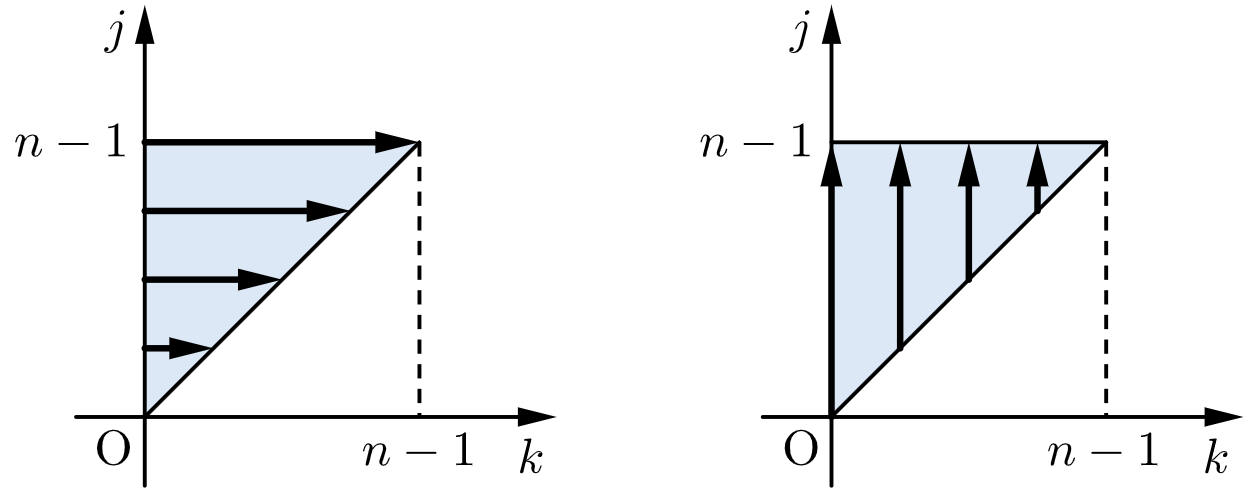
したがって、③より
$$\begin{eqnarray}
&& 1-q_{n+1} \\
&=& p+p^2(1-p) \displaystyle\sum_{j=0}^{n-1} \displaystyle\sum_{k=0}^{j} C_kC_{j-k} \cdot p^j (1-p)^j \\
&=& p+p^2(1-p) \displaystyle\sum_{k=0}^{n-1} \displaystyle\sum_{j=k}^{n-1} C_kC_{j-k} \cdot p^j (1-p)^j \\
&=& p+p^2(1-p) \displaystyle\sum_{k=0}^{n-1} \displaystyle\sum_{j=0}^{n-1-k} C_kC_{j} \cdot p^{j+k} (1-p)^{j+k} \\
&=& p+p^2(1-p) \displaystyle\sum_{k=0}^{n-1} \left\{ C_k \cdot p^k (1-p)^k \displaystyle\sum_{j=0}^{n-1-k} C_j \cdot p^j (1-p)^j \right\}
\end{eqnarray}$$ここで、$0\leqq k \leqq n-1$ の各 $k$ に対して $j=0,1,\cdots,n-1-k$ を代入したものの総和は、下図の網掛け部分（境界を含む。）に含まれるすべての整数の組 $(k,j)$ を代入したものの総和に等しい。

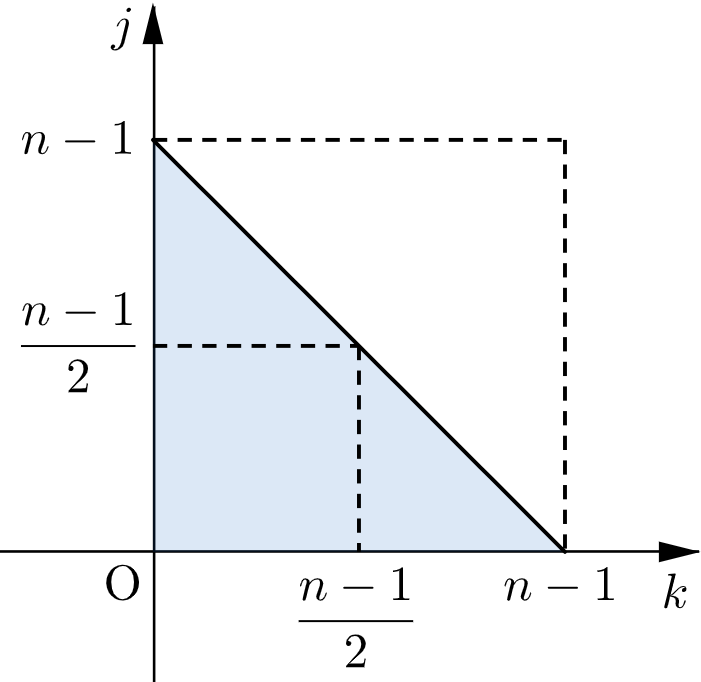
各項は $0$ 以上なので、この総和は「 $0\leqq k \leqq n-1, \ $$0\leqq j \leqq n-1$ を満たすすべての整数の組 $(k,j)$ を代入したものの総和」以下で、かつ「 $0\leqq k \leqq \left\lfloor\dfrac{n-1}{2}\right\rfloor, \ $$0\leqq j \leqq \left\lfloor\dfrac{n-1}{2}\right\rfloor$ を満たすすべての整数の組 $(k,j)$ を代入したものの総和」以上である。ただし、$\lfloor X\rfloor$ は実数 $X$ 以下の最大の整数を表す。

$$\begin{eqnarray}
&& \displaystyle\lim_{n\to\infty} \left[ p+p^2(1-p) \displaystyle\sum_{k=0}^{n-1} \left\{ C_k \cdot p^k (1-p)^k \displaystyle\sum_{j=0}^{n-1} C_j \cdot p^j (1-p)^j \right\} \right] \\
&=& \displaystyle\lim_{n\to\infty} \left[ p+p^2(1-p) \left\{ \displaystyle\sum_{k=0}^{n-1} C_k \cdot p^k (1-p)^k \right\} \left\{ \displaystyle\sum_{j=0}^{n-1} C_j \cdot p^j (1-p)^j \right\} \right] \\
&=& p+p^2(1-p) \cdot \dfrac{a}{p} \cdot \dfrac{a}{p} \\
&=& p+(1-p)a^2
\end{eqnarray}$$であり
$$\begin{eqnarray}
&& \displaystyle\lim_{n\to\infty} \Bigg[ p+p^2(1-p) \displaystyle\sum_{k=0}^{\left\lfloor\frac{n-1}{2}\right\rfloor} \Bigg\{ C_k \cdot p^k (1-p)^k \displaystyle\sum_{j=0}^{\left\lfloor\frac{n-1}{2}\right\rfloor} C_j \cdot p^j (1-p)^j \Bigg\} \Bigg] \\
&=& \displaystyle\lim_{n\to\infty} \Bigg[ p+p^2(1-p) \Bigg\{ \displaystyle\sum_{k=0}^{\left\lfloor\frac{n-1}{2}\right\rfloor} C_k \cdot p^k (1-p)^k \Bigg\} \Bigg\{ \displaystyle\sum_{j=0}^{\left\lfloor\frac{n-1}{2}\right\rfloor} C_j \cdot p^j (1-p)^j \Bigg\} \Bigg] \\
&=& p+p^2(1-p) \cdot \dfrac{a}{p} \cdot \dfrac{a}{p} \\
&=& p+(1-p)a^2
\end{eqnarray}$$であるから、はさみうちの原理により
$$\begin{align}
a &= \displaystyle\lim_{n\to\infty} (1-q_{n+1}) \\
&= \displaystyle\lim_{n\to\infty} \left[ p+p^2(1-p) \displaystyle\sum_{k=0}^{n-1} \left\{ C_k \cdot p^k (1-p)^k \displaystyle\sum_{j=0}^{n-1-k} C_j \cdot p^j (1-p)^j \right\} \right] \\
&= p+(1-p)a^2
\end{align}$$となる。

これを $a$ について解くと
$$\begin{array}{c}
\begin{aligned}
(1-p)a^2 -a +p &=0 \\
(a-1)\{ (1-p)a \ – \ p \} &= 0
\end{aligned}
\\[0.3em]
\therefore \quad a = 1, \ \dfrac{p}{1-p}
\end{array}$$

$\dfrac{1}{2} \lt p \lt 1$ のとき、$\dfrac{p}{1-p} \gt 1$ より $a \leqq 1$ に矛盾するので、$a=1$ である。また、$p=\dfrac{1}{2}$ のときも $a=1$ である。よって、$\dfrac{1}{2} \leqq p \lt 1$ のとき
$$\displaystyle\lim_{n\to\infty} q_n = 1-a = 0$$

また、$0 \lt p \lt \dfrac{1}{2}$ のとき、②より
$$\begin{align}
\displaystyle\lim_{n\to\infty} q_n &= 1-a_p \\
&= 1-\dfrac{p}{1-p}a_{1-p} \\
&= 1-\dfrac{p}{1-p} \cdot 1 \\
&= \dfrac{1-2p}{1-p}
\end{align}$$これは $p=0$ のときも成り立つ。

以上より
$$\displaystyle\lim_{n\to\infty} q_n =
\left\{
\begin{array}{cl}
\boldsymbol{\dfrac{1-2p}{1-p}} & \left( \boldsymbol{0 \leqq p \lt \dfrac{1}{2}} \ \mathbf{\text{のとき}} \right) \\
\boldsymbol{0} & \left( \boldsymbol{\dfrac{1}{2} \leqq p \lt 1} \ \mathbf{\text{のとき}} \right)
\end{array}
\right.
$$

解説

思考力やひらめき、発想の転換が必要な問題で、完答するのは至難の業です。

⑴からヘビーな問題になっています。
二項係数を変形した後は、$\displaystyle\sum_{k=0}^{N-1} p_{n+1,k}$ がどういう値を意味しているか考えましょう。$N\to\infty$ とすると、点列の $y$ 座標はいずれ $0$ となるので、この和は $1$ に収束すると推測できます。確率なので $1$ 以下であることは自明で、あとは下から「 $N\to\infty$ とすれば $1$ に収束する関数」で押さえれば良いことが分かりますが、「 $1$ に収束する関数」というのはつくり出すのが大変です。そこで発想を転換して、$1-\displaystyle\sum_{k=0}^{N-1} p_{n+1,k}$ を上から「 $0$ に収束する関数」で押さえよう、と考えるわけです。

なお、$p_{n+1,k}$ を考えるときには $P_0$ が $(0,n+1)$ となることにも注意が必要です。

⑵は、いわゆる「カタラン数」の問題です。場合分けの方法を知っていないと少し厳しいかもしれません。今回の問題では「点の $y$ 座標が $0$ になったら動かない」ところが一般的なカタラン数を考える上での設定とは異なりますが、条件 $(\mathrm{B})$ を
『条件 $(\mathrm{B}’)$：$P_k(x_k,y_k)$ が $y_k=0$ を満たすならば，$P_{k+1}$ を $(x_k+1,0)$ とおく．』
とすれば、$C_n$ に影響を与えずに一般的な設定と整合させることができるので、漸化式の形も同じものになります。

⑶は、極限の存在についてのただし書きと、⑵で考えた $C_n$ を使って解いていきましょう。

直接 $q_n$ を求めるとなると、最終的に点列がたどり着いた $x$ 軸上の点の $x$ 座標で場合分けすることになりますが、$P_0$ からその点までの経路数はシンプルに表せるものではありません。
そこで、$1-q_{n}$ を考え、領域 $D_n$ の外に出るタイミングで場合分けすれば、経路数が⑵の $C_n$ を用いてシンプルに表せます。
ちなみに、$P_{2j+1}$ の時点で $D_{n+1}$ の外に出ているので、そこから後の点をいくら考えても「点列の点のうちいずれかが $D_{n+1}$ に属さない」ということは変わりません。よって、数えるべき点列は $P_0$ から $P_{2j}$（ $P_{2j+1}$ ）までで良いと分かります。

$a_p$ を別の方法で表すために、$\displaystyle\sum$ の変数をうまく変換する必要があります。$\displaystyle\sum$ が $2$ つあるときは別の和のとり方をしてみましょう。本問のように見通しが良くなる場合があります。

補足

〔1〕
$$\displaystyle \lim_{N\to\infty} \dfrac{(n+N)^{n+1}}{2^{n+N}} = 0 \quad\cdots(*)$$を示します。

十分大きい $N$ をとると $n\lt N$ より
$$\begin{align}
\dfrac{(n+N)^{n+1}}{2^{n+N}} &\lt \dfrac{(N+N)^{n+1}}{2^{n+N}} \\
&= 2 \cdot \dfrac{N^{n+1}}{2^N}
\end{align}$$なので、$\displaystyle\lim_{N\to\infty}\dfrac{N^{n+1}}{2^N}=0$ を示せばよいです。

十分大きい $N$ をとると $N \gt n+2$ より、二項定理を用いると
$$\begin{align}
2^N &= (1+1)^N \\
&= \displaystyle\sum_{k=0}^{N}{}_N\mathrm{C}_k \gt \displaystyle\sum_{k=0}^{n+2}{}_N\mathrm{C}_k
\end{align}$$が成り立つので
$$\dfrac{N^{n+1}}{2^N} \lt \dfrac{N^{n+1}}{\displaystyle\sum_{k=0}^{n+2}{}_N\mathrm{C}_k}$$となります。この式で $N\to\infty$ とすると、$\displaystyle\sum_{k=0}^{n+2}{}_N\mathrm{C}_k$ は $N$ の $(n+2)$ 次式であることから右辺は（分母の方が次数が高く）$0$ に収束するので、左辺も $0$ に収束します。よって、$(*)$ が示されました。
（解答へ戻る）

まとめ

今回は、京都大学理学部特色入試・数学（2022年度 第4問）の解説をしました。