今回は、京都大学理学部特色入試・数学(2022年度 第2問)の解説をしたいと思います。
問題
半径 $1$ の円 $C$ の周上に相異なる $5$ 点 $A_1,$ $A_2,$ $A_3,$ $A_4,$ $A_5$ がこの順に並んでいるとし,
$$\begin{array}{l}
B_1 \ \text{を線分} \ A_1A_3 \ \text{と線分} \ A_2A_4 \ \text{の交点,} \\
B_2 \ \text{を線分} \ A_2A_4 \ \text{と線分} \ A_3A_5 \ \text{の交点,} \\
B_3 \ \text{を線分} \ A_3A_5 \ \text{と線分} \ A_4A_1 \ \text{の交点,} \\
B_4 \ \text{を線分} \ A_4A_1 \ \text{と線分} \ A_5A_2 \ \text{の交点,} \\
B_5 \ \text{を線分} \ A_5A_2 \ \text{と線分} \ A_1A_3 \ \text{の交点} \\
\end{array}$$とするとき,
$$\begin{array}{l}
S_1 \ \text{を} \ \triangle A_1B_5B_4 \ \text{の面積,} \\
S_2 \ \text{を} \ \triangle A_2B_1B_5 \ \text{の面積,} \\
S_3 \ \text{を} \ \triangle A_3B_2B_1 \ \text{の面積,} \\
S_4 \ \text{を} \ \triangle A_4B_3B_2 \ \text{の面積,} \\
S_5 \ \text{を} \ \triangle A_5B_4B_3 \ \text{の面積,} \\
T \ \text{を五角形} \ B_1B_2B_3B_4B_5 \ \text{の面積}
\end{array}$$とおく.このように $A_1,$ $A_2,$ $A_3,$ $A_4,$ $A_5$ を動かしたとき,
$$S=S_1+S_2+S_3+S_4+S_5+2T$$の最大値を求めよ.ただし,三角比の値は具体的に求めずに用いてよい.
(京都大学)
解答
円 $C$ の中心を $O$ とする。図は次のようになる。
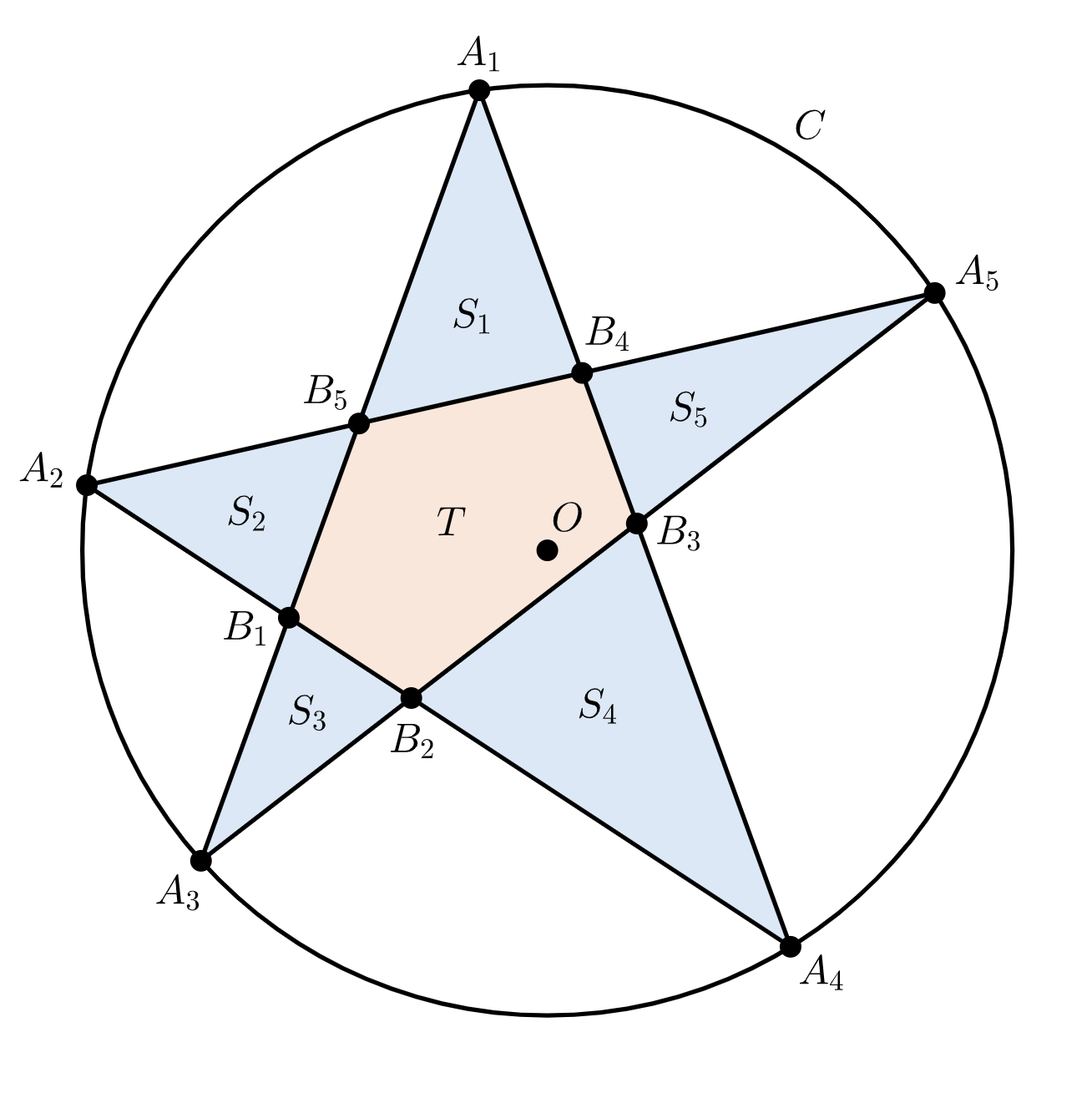
$S$ が最大となるとき、五角形 $A_1A_2A_3A_4A_5$ は正五角形となることを示す。
なお、$S$ は $5$ 点 $A_1,$ $A_2,$ $A_3,$ $A_4,$ $A_5$ を動かすと連続的に変化し最大値が存在するので、正五角形でない五角形 $A_1A_2A_3A_4A_5$ で $S$ が最大となるという仮定が矛盾することを示せばよい。
五角形 $A_1A_2A_3A_4A_5$ が正五角形であるとき、$\triangle A_1A_3A_4$ は $\angle A_1A_3A_4 = \angle A_1A_4A_3$ の三角形であり、同様に、ある点とそこから反時計回りに数えて $2,3$ 個目の点を $3$ 頂点とする他の $4$ 個の三角形は、隣り合った(他の点を含まないような弧をとりうる)$2$ 点での内角が等しい三角形である。以下、このように選んだ三角形を▲で表す。
ここで、正五角形でない五角形 $A_1A_2A_3A_4A_5$ は、$5$ 個の▲のうち、隣り合った $2$ 点での内角が等しくないものが少なくとも $1$ 個存在することを示す。
その上で、正五角形でない五角形 $A_1A_2A_3A_4A_5$ で、すべての▲について隣り合った $2$ 点での内角が等しいものが存在すると仮定する。
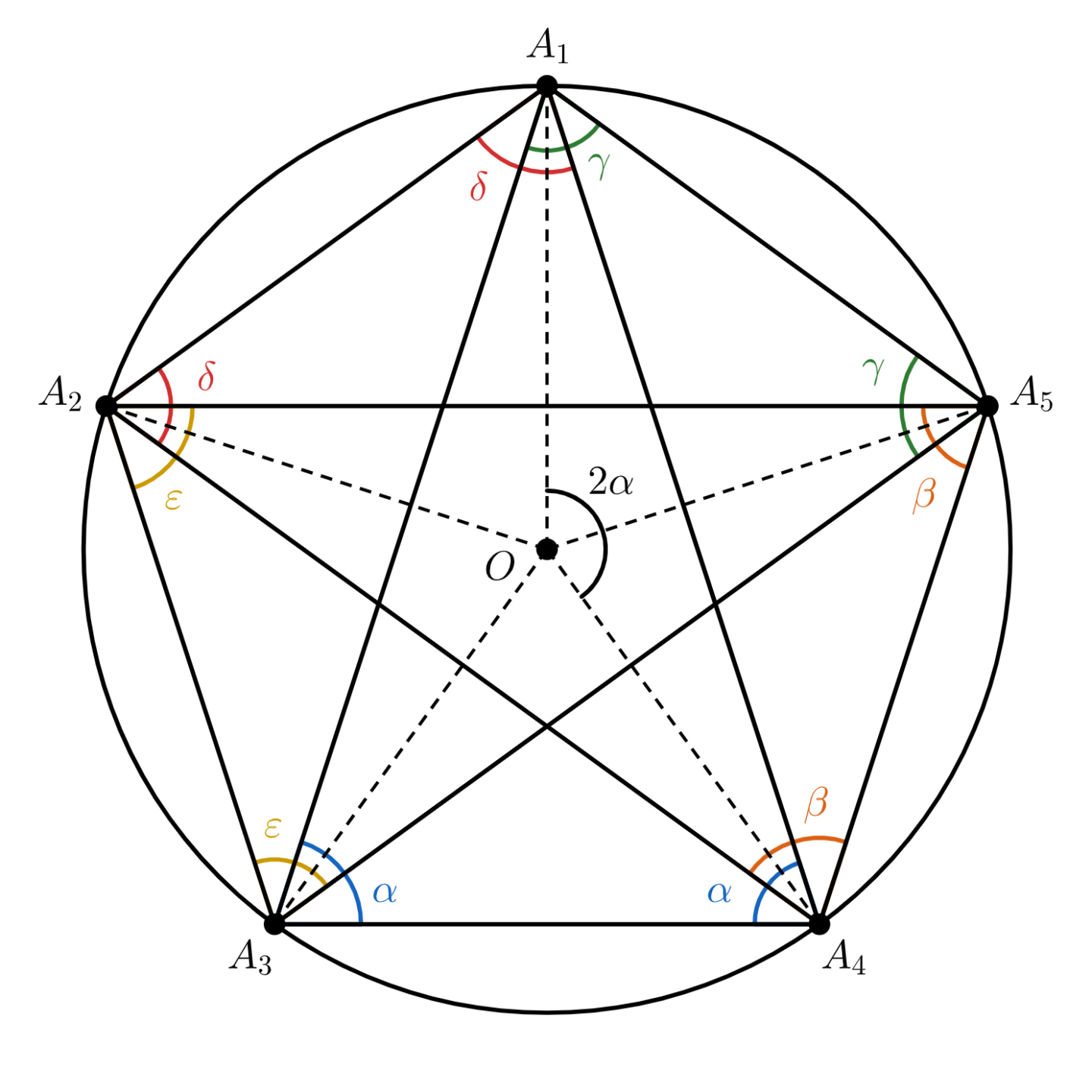
$$\begin{align}
\angle A_1A_3A_4 &= \angle A_1A_4A_3 = \alpha \\
\angle A_2A_4A_5 &= \angle A_2A_5A_4 = \beta \\
\angle A_3A_5A_1 &= \angle A_3A_1A_5 = \gamma \\
\angle A_4A_1A_2 &= \angle A_4A_2A_1 = \delta \\
\angle A_5A_2A_3 &= \angle A_5A_3A_2 = \varepsilon
\end{align}$$とおくと、点 $A_5$ を含む弧 $A_1A_4$ に対する円周角より $\alpha = \delta$ である。同様に考えると
$$\alpha = \beta = \gamma = \delta = \varepsilon \quad\cdots\text{①}$$が成り立つ。ここで、点 $A_5$ を含む弧 $A_1A_4$ に対する円周角と中心角より $\angle A_1OA_4 = 2\alpha$ である。同様に考えると
$$\begin{eqnarray}
&& 2 \cdot 360^\circ \\
&=& \angle A_1OA_4 + \angle A_2OA_5 + \angle A_3OA_1 + \angle A_4OA_2 + \angle A_5OA_1 \\
&=& 2\alpha + 2\beta + 2\gamma + 2\delta + 2\varepsilon
\end{eqnarray}$$が成り立ち、①より
$$\alpha = \beta = \gamma = \delta = \varepsilon = 72^\circ$$となる。よって
$$\begin{align}
\angle A_5A_1A_2 &= \angle A_3A_1A_5 + \angle A_4A_1A_2 \ – \ \angle A_3A_1A_4 \\
&= \gamma + \delta \ – \ (180^\circ – \ 2\alpha) \\
&= 108^\circ
\end{align}$$となり、同様に
$$\angle A_1A_2A_3 = \angle A_2A_3A_4 = \angle A_3A_4A_5 = \angle A_4A_5A_1 = 108^\circ$$となるので、五角形 $A_1A_2A_3A_4A_5$ は正五角形となるが、これは仮定に反する。
したがって、背理法より、正五角形でない五角形 $A_1A_2A_3A_4A_5$ で、すべての▲について隣り合った $2$ 点での内角が等しいものは存在しない。すなわち、正五角形でない五角形 $A_1A_2A_3A_4A_5$ は、$5$ 個の▲のうち、隣り合った $2$ 点での内角が等しくないものが少なくとも $1$ 個存在する。
このとき、$\triangle A_1A_3A_4$ において $\angle A_1A_3A_4 \ne \angle A_1A_4A_3$ としても一般性を失わない。これは、点 $A_1$ が線分 $A_3A_4$ の垂直二等分線上にないことと同値である。
線分 $A_3A_4$ の垂直二等分線と点 $A_1$ を含む弧 $A_3A_4$ の交点を $A_1’$ とすると、図は次のようになる。
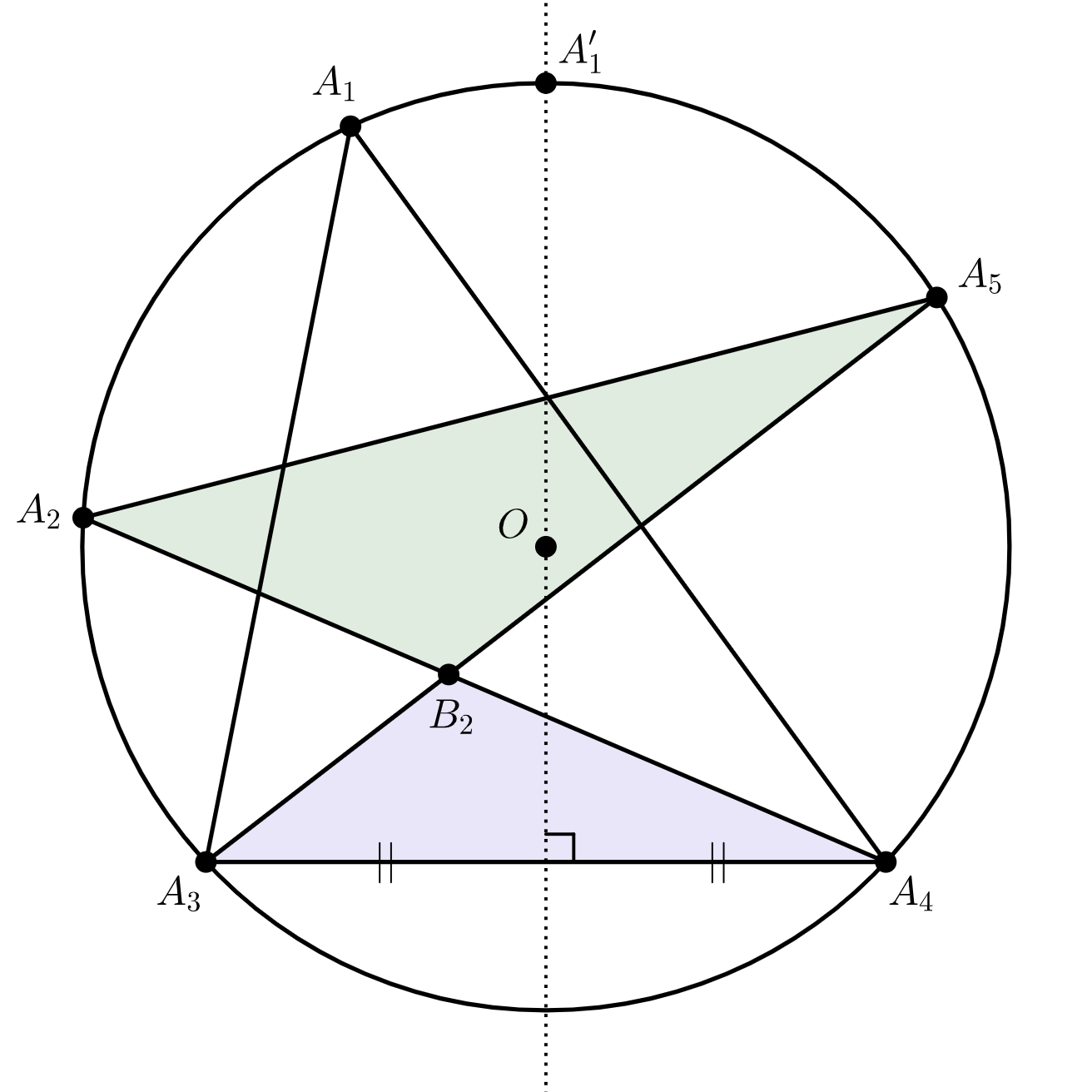
$\triangle PQR$ の面積を $|\triangle PQR|$ で表すとすると
$$S = |\triangle A_1A_3A_4| + |\triangle A_2B_2A_5| \ – \ |\triangle A_3B_2A_4|$$が成り立つ。
ここで、点 $A_2,$ $A_3,$ $A_4,$ $A_5$ を固定し、点 $A_1$ のみを動かす場合を考えると、線分 $A_2A_4,$ $A_2A_5,$ $A_3A_4,$ $A_3A_5$ は動かないので、$|\triangle A_2B_2A_5|,$ $|\triangle A_3B_2A_4|$ は一定である。すなわち、$S$ の大小は $|\triangle A_1A_3A_4|$ の大小と一致する。
$\triangle A_1A_3A_4$ の底辺を線分 $A_3A_4$ として考えると、点 $A_1$ を点 $A_1’$ の方へ動かすことによって $\triangle A_1A_3A_4$ の高さが大きくなり、$|\triangle A_1A_3A_4|$ を大きくすることができる。なおこれは、点 $A_1$ を含む弧 $A_2A_5$ が点 $A_1’$ を含まない下図のような場合でも成り立つ。
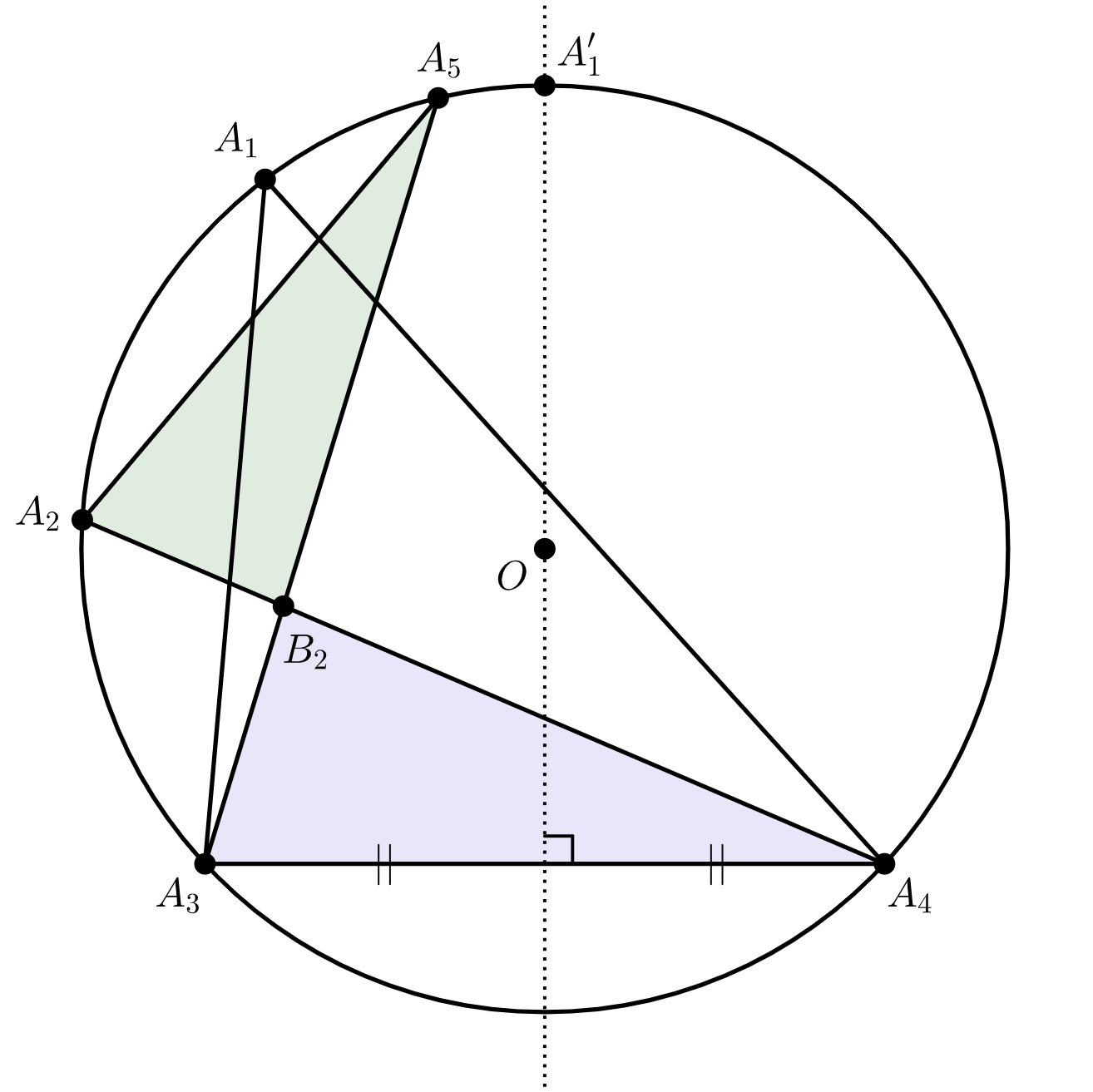
以上より、$S$ が最大となるときの五角形 $A_1A_2A_3A_4A_5$ が正五角形でないと仮定すると、▲のうち隣り合った $2$ 点での内角が等しくないものが存在し、残りの $1$ つの内角が位置する頂点を(他の $4$ 点を固定したまま)その▲の底辺の垂直二等分線上の点の方へ動かすことで $S$ を大きくすることができるので、矛盾する。
よって、$S$ が最大となるのは、五角形 $A_1A_2A_3A_4A_5$ が正五角形のときである。
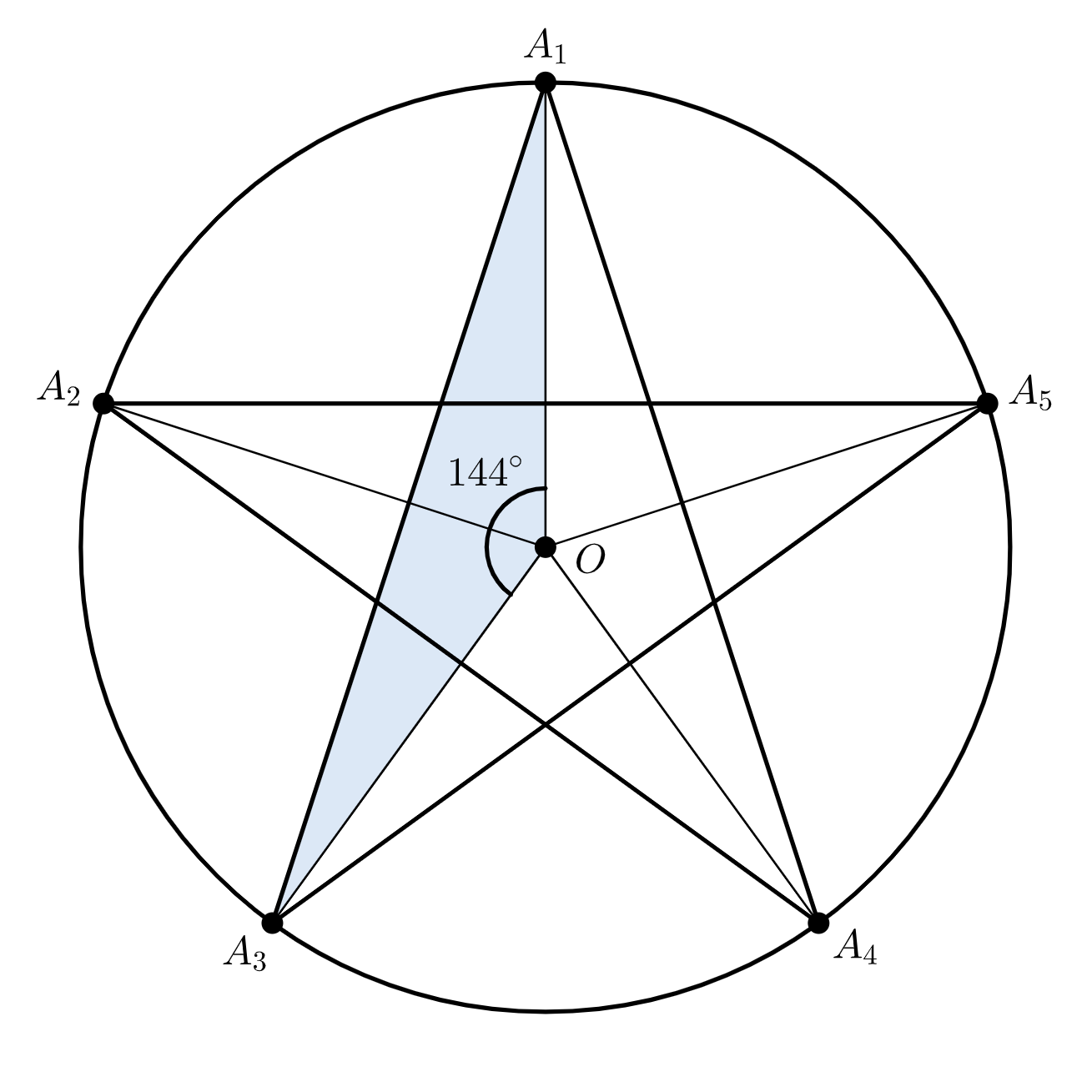
五角形 $A_1A_2A_3A_4A_5$ が正五角形のとき
$$\angle A_1OA_3 = \dfrac{360^\circ}{5}\cdot 2 = 144^\circ$$であり、同様に考えると
$$\begin{align}
S &= |\triangle A_1OA_3| + |\triangle A_2OA_4| + |\triangle A_3OA_5| + |\triangle A_4OA_1| + |\triangle A_5OA_2| \\
&= 5 \cdot \dfrac{1}{2} \cdot 1^2 \cdot \sin 144^\circ \\
&= \boldsymbol{ \dfrac{5}{2}\sin 36^\circ }
\end{align}$$
$$\boldsymbol{ \dfrac{5}{2}\sin 36^\circ }$$
解説
図を描くと状況はすぐ分かると思います。抽象的な問題設定なので、すぐ座標平面に持ち込みたくなりますが、変数の数が多くなり大変そうです。座標は最終手段に取っておいて、幾何で分かることはないか、試行錯誤しながら手がかりを探しましょう。
$S$ が最大になるとき、五角形 $A_1A_2A_3A_4A_5$ は正五角形なのではないか、と何となく推測できるかもしれませんが、それを示すのがこの問題の最大のテーマです。
本解答では、$S$ が最大のときの五角形 $A_1A_2A_3A_4A_5$ が正五角形でないとすると、より大きな $S$ が得られるので、最大の $S$ と言っていたことに矛盾する=仮定が間違っていた(五角形 $A_1A_2A_3A_4A_5$ は正五角形だった)という背理法を使いました。
矛盾を示す上で、本解答では「ある五角形が正五角形でないならば、$5$ つの▲のうち、隣り合った $2$ 点での内角が等しくないものが少なくとも $1$ つ存在する」ことを用いましたが、他にも使える性質はあります。以下、矛盾を示す際の別解を示します:
五角形 $A_1A_2A_3A_4A_5$ が正五角形であるとき、点 $A_1$ は辺 $A_3A_4$ の垂直二等分線上にあり、他の $4$ 個の頂点も同様に、自身と両隣を除く $2$ 点を両端とする線分(以下、対辺という。)の垂直二等分線上にある。
ここで、正五角形でない五角形 $A_1A_2A_3A_4A_5$ は、$5$ 個の頂点のうち、対辺の垂直二等分線上にないものが少なくとも $1$ 個存在することを示す。
その上で、正五角形でない五角形 $A_1A_2A_3A_4A_5$ で、すべての頂点が対辺の垂直二等分線上にあるものが存在すると仮定する。
線分 $A_1A_2,$ $A_3A_4,$ $A_4A_5,$ $A_5A_1$ の中点をそれぞれ $D,$ $E,$ $F,$ $G$ とすると、円 $C$ の弦の垂直二等分線は中心 $O$ を通るので、仮定より直線 $A_1E,$ $A_2G,$ $A_4D$ はすべて点 $O$ を通り
$$\begin{array}{l}
\angle A_1DA_4 = \angle A_1EA_4 = \angle A_1GA_3 = 90^\circ, \\
A_1D=A_2D, \ A_3E=A_4E, \ A_5G=A_1G
\end{array}$$となる。特に、点 $A_1$ は線分 $A_3A_4$ の垂直二等分線上にあるので
$$\angle A_3A_1O=\angle A_4A_1O = \theta$$とおけ、図は次のようになる。
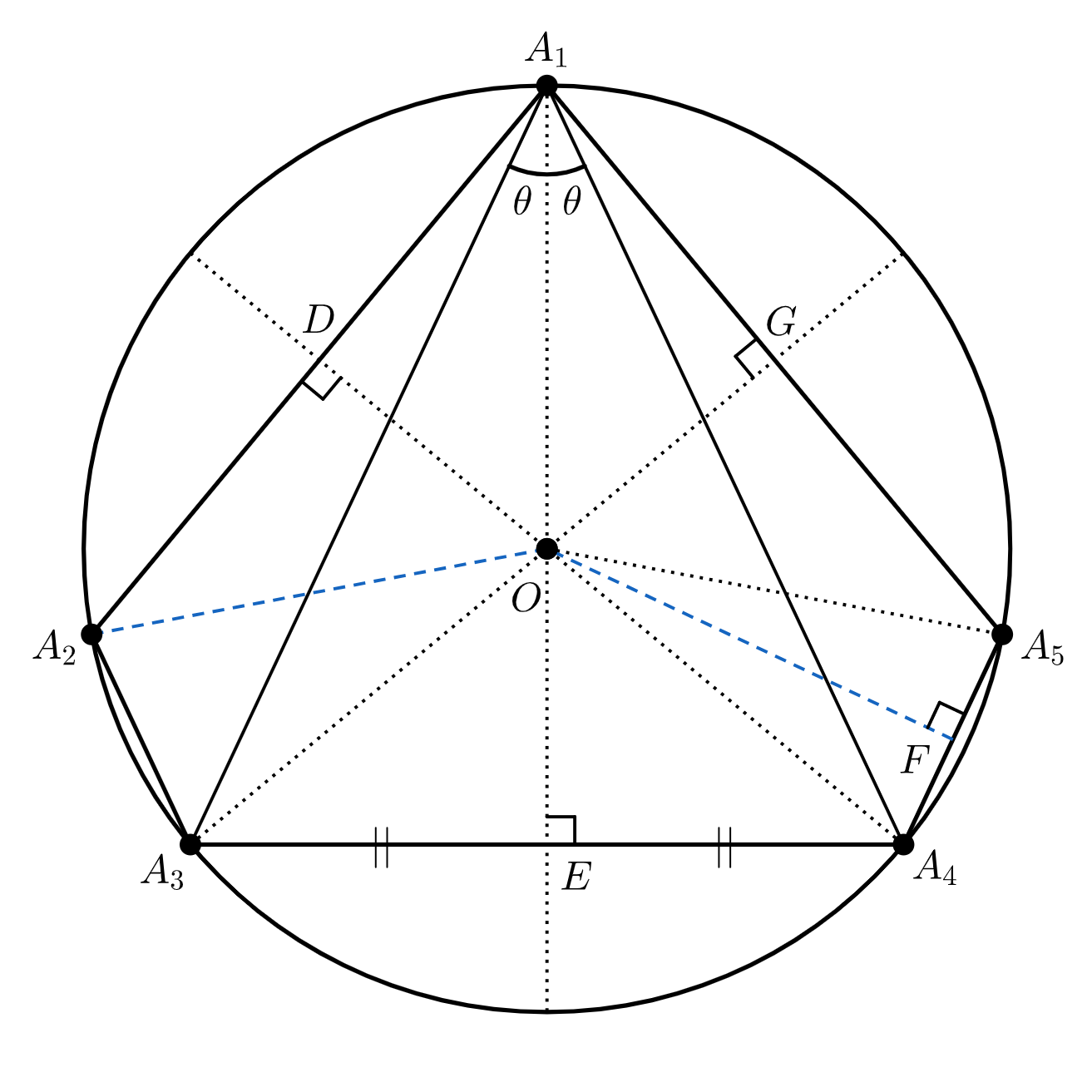
このとき、中心角と円周角の関係より
$$\angle A_3OE = \angle A_4OE = 2\theta$$対頂角より
$$\begin{array}{l}
\angle A_1OD = \angle A_4OE = 2\theta \\
\angle A_1OG = \angle A_3OE = 2\theta
\end{array}$$$$\angle A_1OD+\angle DA_1O = \angle A_1OG+\angle GA_1O = 90^\circ$$より
$$\angle A_2A_1A_3 = \angle A_4A_1A_5 = 90^\circ – \ 3\theta$$中心角と円周角の関係より
$$\angle A_2OA_3 = \angle A_4OA_5 = 180^\circ – \ 6\theta$$直線 $OF$ は線分 $A_4A_5$ の垂直二等分線なので
$$\angle A_4OF = 90^\circ -3\theta$$となる。
ここで、$\theta$ の存在範囲として、$\theta\gt 0^\circ$ かつ $90^\circ – \ 3\theta \gt 0$ すなわち
$$0^\circ \lt \theta \lt 30^\circ \quad\cdots(*)$$が必要である。逆に $\theta$ が $(*)$ の範囲を満たすとき、先の議論に用いた角度はすべて $0^\circ$ より大きく $180^\circ$ 未満の範囲を動くので、矛盾なく議論することができる。すなわち、$\theta$ の存在範囲は $(*)$ である。
このとき、点 $A_2$ は線分 $A_4A_5$ の垂直二等分線上にあり、これは点 $O$ を通るので、$\angle A_2OF = 180^\circ$ となる。これを $\theta$ について解くと
$$\begin{align}
180^\circ &= \angle A_2OF \\
&= \angle A_2OA_3 + \angle A_3OE +\angle EOA_4 +\angle A_4OF \\
&= (180^\circ – \ 6\theta) + 2\theta+ 2\theta + (90^\circ -3\theta) \\
&= 270^\circ – \ 5\theta \\[0.5em]
\therefore \ \theta &= 18^\circ
\end{align}$$となり、これは $(*)$ を満たす。
また
$$\begin{align}
\angle A_5A_1A_2 &= 2(\angle OA_1A_3 + \angle A_2A_1A_3) \\
&= 2(\theta + 90^{\circ} -3\theta ) \\
&= 108^\circ \\[0.3em]
\angle A_1A_2A_3 &= \angle OA_2A_1 + \angle OA_2A_3 \\
&= (90^{\circ} -2\theta) + \dfrac{180^{\circ} – \ (180^{\circ} – \ 6\theta)}{2} \\
&= 108^\circ \\[0.3em]
\angle A_2A_3A_4 &= \angle OA_3A_1 + \angle OA_3E \\
&= \dfrac{180^{\circ} – \ (180^{\circ} – \ 6\theta)}{2} + (90^\circ -2\theta) \\
&= 108^\circ \\[0.3em]
\angle A_3A_4A_5 &= \angle A_2A_3A_4 =108^\circ \\[0.3em]
\angle A_4A_5A_1 &= \angle A_1A_2A_3 =108^\circ
\end{align}$$より、五角形 $A_1A_2A_3A_4A_5$ は正五角形となるが、これは五角形 $A_1A_2A_3A_4A_5$ が正五角形でないとする仮定に反する。よって背理法より、正五角形でない五角形 $A_1A_2A_3A_4A_5$ で、すべての頂点が対辺の垂直二等分線上にあるものは存在しない。
すなわち、正五角形でない五角形 $A_1A_2A_3A_4A_5$ は、$5$ 個の頂点のうち、対辺の垂直二等分線上にないものが少なくとも $1$ 個存在する。
五角形 $A_1A_2A_3A_4A_5$ が正五角形だと示せたら、あとは計算です。解答のようにうまく $S$ を計算しやすい図形に分けて計算量を減らして解きましょう。
余談ですが、$\sin 36^\circ = \dfrac{\sqrt{10-2\sqrt{5}}}{4}$ です。
まとめ
今回は、京都大学理学部特色入試・数学(2022年度 第2問)の解説をしました。
ほかの問題にもチャレンジしよう!
京都大学 理学部特色入試(数学)2022年度 第1問 解説
京都大学 理学部特色入試(数学)2022年度 第2問 解説
京都大学 理学部特色入試(数学)2022年度 第3問 解説
京都大学 理学部特色入試(数学)2022年度 第4問 解説













