今回は、一橋大学数学(2021年 第1問)の解説をしたいと思います。
問題
$1000$ 以下の素数は $250$ 個以下であることを示せ。
(一橋大学)
解答
$1$ は素数でないので、「$\,2$ 以上 $1000$ 以下の整数のうち、合成数が $749$ 個以上あること」$\cdots(*)$ を示せばよい。
ここで、集合 $U$ を
$$U=\{\,x\mid2\leqq x\leqq1000, \ x\,\text{は整数}\,\}$$と定義し、$U$ の部分集合 $A,\,$$B,\,$$C$ を
$$\begin{align}
A &= \{\,x\mid2\leqq x\leqq1000, \ x\,\text{は}\,2\,\text{の倍数}\,\}, \\[0.2em]
B &= \{\,x\mid2\leqq x\leqq1000, \ x\,\text{は}\,3\,\text{の倍数}\,\}, \\[0.2em]
C &= \{\,x\mid2\leqq x\leqq1000, \ x\,\text{は}\,5\,\text{の倍数}\,\}
\end{align}$$によって定める。
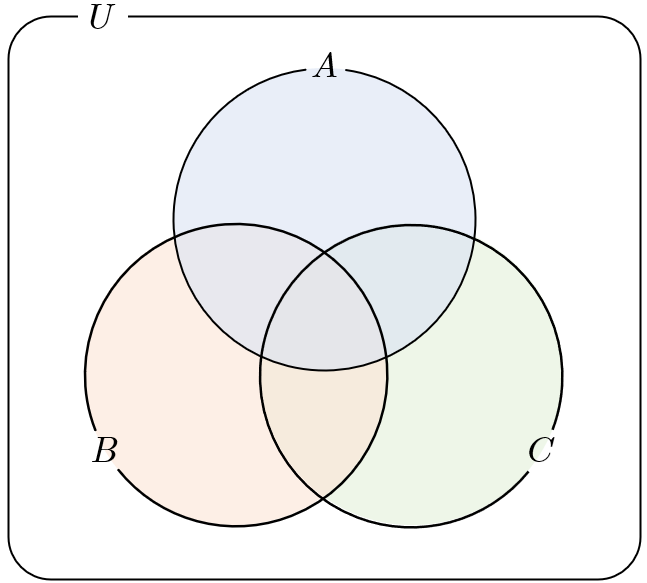
集合 $X$ の要素の個数を $n(X)$ で表すとすると
$$n(A)=500,\quad n(B)=333,\quad n(C)=200$$である。
また
$$\begin{align}
A\cap B &= \{\,x\mid2\leqq x\leqq1000, \ x\,\text{は}\,6\,\text{の倍数}\,\}, \\[0.2em]
B\cap C &= \{\,x\mid2\leqq x\leqq1000, \ x\,\text{は}\,15\,\text{の倍数}\,\}, \\[0.2em]
C\cap A &= \{\,x\mid2\leqq x\leqq1000, \ x\,\text{は}\,10\,\text{の倍数}\,\}, \\[0.2em]
A\cap B\cap C &= \{\,x\mid2\leqq x\leqq1000, \ x\,\text{は}\,30\,\text{の倍数}\,\}
\end{align}$$であるから
$$\begin{array}{ll}
n(A\cap B)=166, & n(B\cap C)=66, \\[0.2em]
n(C\cap A)=100, & n(A\cap B\cap C)=33
\end{array}$$となる。
したがって
$$\begin{array}{l}
\hphantom{=} \ n(A\cup B\cup C) \\[0.2em]
=n(A)+n(B)+n(C) \\
\hphantom{=} -n(A\cap B)-n(B\cap C)-n(C\cap A) \\
\hphantom{=} +n(A\cap B\cap C) \\[0.2em]
=500+333+200-166-66-100+33 \\[0.2em]
=734
\end{array}$$となる。
よって、集合 $A\cup B\cup C$ の要素のうち、素数である $2,\,$$3,\,$$5$ を除く $731$ 個は合成数である。$\cdots\text{①}$
次に、$2,\,3,\,5$ のいずれの倍数でもない合成数として、$7$ 以上の素数 $2$ つの積を考える。
$7,\,$$11,\,$$13,\,$$17,\,$$19,\,$$23$ の $6$ 個の整数から重複を許して選んだ $2$ 個の積は、$7^2=49$ 以上、$23^2=529$ 以下の整数であるから集合 $U$ に属し、その数は
$$6+{}_6\mathrm{C}_2=21 \quad\cdots\text{②}$$である。
①,②より、$2$ 以上 $1000$ 以下の合成数は少なくとも $731+21=752$ 個あり、$(*)$ が成り立つので、題意は示された。$$\tag{証明終}$$
解説
$2,\,3,\,5,\,7,\,\cdots$ と素数を書き上げるのは途方もない作業なので、逆転の発想をして、素数でない数(=$1$ と合成数)が $750$ 個以上あることを示します。
$1000$ 以下の自然数のうち、$2$ の倍数は $500$ 個、$3$ の倍数は $333$ 個…と考えると、ベン図を発想すると思います。本問は、それに気付けるかがポイントでした。
解答は $3$ つの部分集合を用いて解きました。$4$ つでやれば一発で $749$ 個を超えていたのでは?と思うかもしれませんが、$4$ つの部分集合によるベン図は複雑(下図参照)で、それに応じて計算式も複雑になるので、$3$ つで考えるのが安全だと思います。
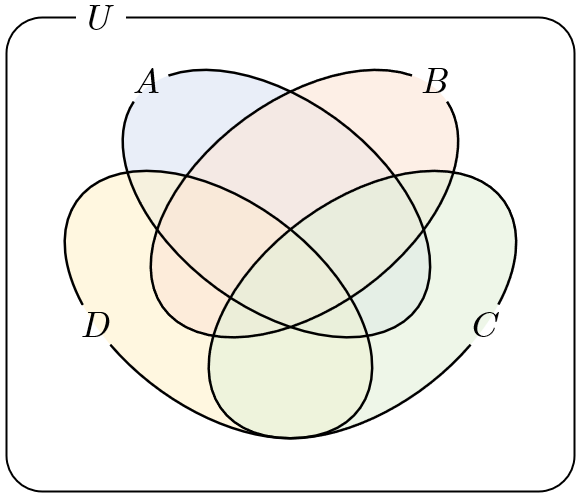
$4$ つの集合 $A,\,B,\,C,\,D$ の要素数について
$$\begin{array}{l}
\hphantom{=} \ n(A\cup B\cup C\cup D) \\[0.2em]
=n(A)+n(B)+n(C)+n(D) \\
\hphantom{=} -n(A\cap B)-n(B\cap C)-n(C\cap D) \\
\hphantom{=} -n(D\cap A)-n(A\cap C)-n(B\cap D) \\
\hphantom{=} +n(A\cap B\cap C)+n(B\cap C\cap D) \\
\hphantom{=} +n(C\cap D\cap A)+n(D\cap A\cap B) \\
\hphantom{=} -n(A\cap B\cap C\cap D)
\end{array}$$が成り立つ。
$2,\,3,\,5$ の倍数をすべて排除したら、残りの不足分は $7\times7$ や $11\times13$ など、もっと大きな素数どうしの積で補いましょう。
ちなみに、$1000$ 以下の素数は $168$ 個あるそうです。こうしてみると $250$ 個以下というのは優しめの設定なんですね。
まとめ
今回は、一橋大学数学(2021年 第1問)の解説をしました。
ほかの問題にもチャレンジしよう!
一橋大学 数学 2021年 第1問 解説
一橋大学 数学 2021年 第2問 解説
一橋大学 数学 2021年 第3問 解説
一橋大学 数学 2021年 第4問 解説
一橋大学 数学 2021年 第5問 解説













