一橋大学 数学 2021年 第4問 解説

今回は、一橋大学数学（2021年 第4問）の解説をしたいと思います。

問題

　$k\gt0$ とする。円 $C$ を $x^2+(y-1)^2=1$ とし，放物線 $S$ を $y=\dfrac{1}{k}x^2$ とする。

⑴　$C$ と $S$ が共有点をちょうど $3$ 個持つときの $k$ の範囲を求めよ。

⑵　$k$ が⑴の範囲を動くとき，$C$ と $S$ の共有点のうちで $x$ 座標が正の点を $\mathrm{P}$ とする。$\mathrm{P}$ における $S$ の接線と $S$ と $y$ 軸とによって囲まれる領域の面積の最大値を求めよ。

（一橋大学）

解答

⑴

$C$ と $S$ の式から $y$ を消去すると
$$x^2+\left(\dfrac{1}{k}x^2-1\right)^2=1 \quad\cdots\text{①}$$となり、この解は $C$ と $S$ の共有点の $x$ 座標を表す。

①より
$$\begin{array}{c}
\begin{align}
\dfrac{1}{k^2}x^4+\left(1-\dfrac{2}{k}\right)x^2 &= 0 \\[0.2em]
x^2\left(\dfrac{1}{k^2}x^2+1-\dfrac{2}{k}\right) &= 0
\end{align} \\[0.2em]
\therefore \ x=0,\quad x^2=k(2-k)
\end{array}$$

題意を満たすのは $x^2=k(2-k)$ が $x=0$ 以外で異なる $2$ つの実数解をもつときであり、その条件は
$$\begin{array}{c}
k(2-k)\gt0 \\[0.3em]
\therefore \ \boldsymbol{0\lt k\lt2}
\end{array}$$

⑵

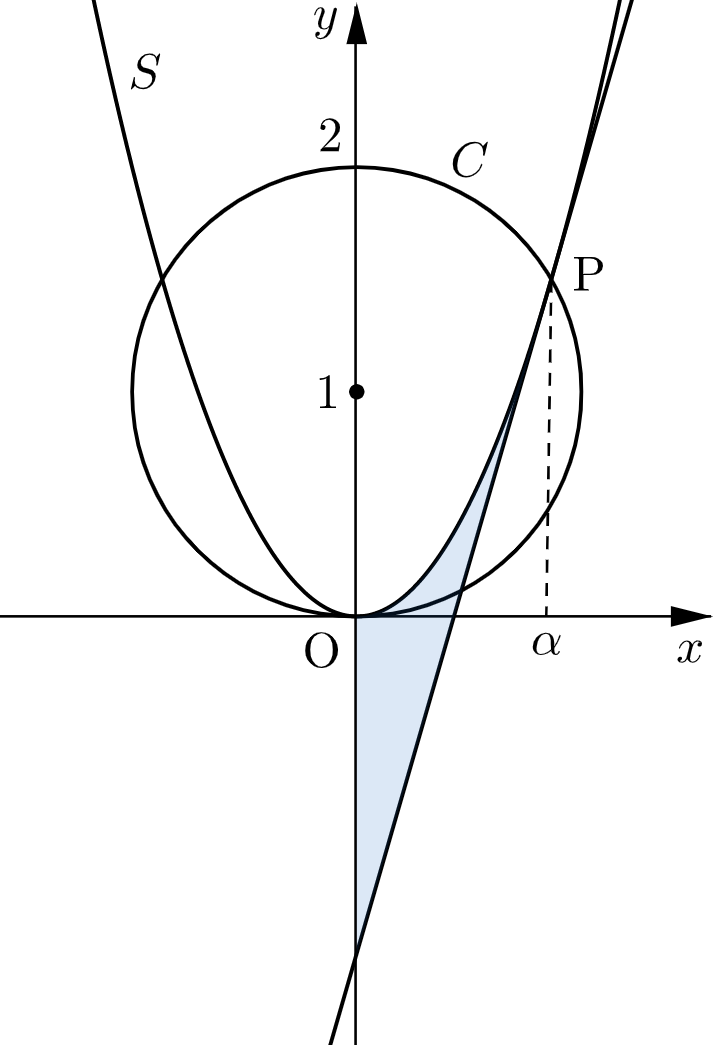
$\dfrac{d}{dx}\left(\dfrac{1}{k}x^2\right)=\dfrac{2}{k}x$ より、点 $\mathrm{P}$ における $S$ の接線の方程式は
$$\begin{align}
y &= \dfrac{2}{k}\alpha\cdot(x-\alpha)+\dfrac{1}{k}\alpha^2 \\[0.2em]
\therefore \ y &= \dfrac{2\alpha}{k}x-\dfrac{1}{k}\alpha^2
\end{align}$$となる。

題意の面積を $S$ とすると
$$\begin{align}
S &= \displaystyle\int_{0}^{\alpha}\left(\dfrac{1}{k}x^2-\dfrac{2\alpha}{k}x+\dfrac{1}{k}\alpha^2\right)dx \\[0.2em]
&= \dfrac{1}{k}\displaystyle\int_{0}^{\alpha}(x-\alpha)^2dx \\[0.2em]
&= \dfrac{1}{3k}\Big[(x-\alpha)^3\Big]_{0}^{\alpha} \\[0.2em]
&= \dfrac{\alpha^3}{3k} \\[0.2em]
&= \dfrac{k(2-k)\sqrt{k(2-k)}}{3k} \\[0.2em]
&= \dfrac{\sqrt{k(2-k)^3}}{3}
\end{align}$$

$f(k)=k(2-k)^3$ とおくと
$$\begin{align}
f'(k) &= (2-k)^3+k\cdot3(2-k)^2\cdot(-1) \\
&= (2-k)^2(2-k-3k) \\
&= 2(2-k)^2(1-2k)
\end{align}$$より、$0\lt k\lt2$ における $f(k)$ の増減表は次のようになる。
$$\begin{array}{c|c|c|c|c|c} \hline
k & (0) & \cdots & \dfrac{1}{2} & \cdots & (2) \\ \hline
f'(k) & & + & 0 & – & \\ \hline
f(k) & & \nearrow & \dfrac{27}{16} & \searrow & \\ \hline
\end{array}$$

よって、$k=\dfrac{1}{2}$ のとき $f(k)$ は最大値 $\dfrac{27}{16}$ をとる。

$S=\dfrac{\sqrt{f(k)}}{3}$ より、$f(k)$ が最大となるとき $S$ も最大となるので、求める最大値は
$$\dfrac{1}{3}\cdot\sqrt{\dfrac{27}{16}}=\boldsymbol{\dfrac{\sqrt{3}}{4}}$$

解説

⑴は、$C$ と $S$ がともに $y$ 軸対称であるということから、$x^2$ を消去した式
$$ky+(y-1)^2=1$$からスタートしても大丈夫です。

いずれにせよ、円と曲線（$\,2$ 次関数や $3$ 次関数）の共有点の問題で「図より」とするのはやめておいた方がよいです。

というのも、円と曲線の共有点近傍は、図では厳密に議論できないからであり、方程式から論理的に説明するのがベストだからです。

⑵は、微分・積分の計算がきちんとできるか問われています。

なお、解答では文系では習わない「（単純な）置換積分」と「合成関数の微分」を用いています。文系の範囲で済ませたければ、展開して計算しましょう。

まとめ

今回は、一橋大学数学（2021年 第4問）の解説をしました。