今回は、一橋大学数学(2021年 第3問)の解説をしたいと思います。
問題
次の問いに答えよ。
⑴ $a,\,b$ を実数とし,$2$ 次方程式 $x^2-ax+b=0$ が実数解 $\alpha,\,$$\beta$ をもつとする。ただし,重解の場合は $\alpha=\beta$ とする。$3$ 辺の長さが $1,\,$$\alpha,\,$$\beta$ である三角形が存在する $(a,\,b)$ の範囲を求め図示せよ。
⑵ $3$ 辺の長さが $1,\,$$\alpha,\,$$\beta$ である三角形が存在するとき,
(一橋大学)
$$\dfrac{\alpha\beta+1}{(\alpha+\beta)^2}$$の値の範囲を求めよ。
解答
⑴
$x^2-ax+b=0$ が $2$ つの実数解をもつとき、$(\text{判別式})\geqq0$ より
$$\begin{align}
a^2-4b &\geqq 0 \\[0.2em]
\therefore \ b &\leqq \dfrac{1}{4}a^2 \quad\cdots\text{①}
\end{align}$$
解と係数の関係より
$$\left\{\begin{align}
\alpha+\beta &= a \\
\alpha\beta &= b
\end{align}\right. \quad\cdots\text{②}$$
ここで、$\alpha,\,\beta$ は三角形の辺の長さなので $\alpha\gt0$,$\beta\gt0$ となり、①より
$$a\gt0,\quad b\gt0 \quad\cdots\text{③}$$
三角形の成立条件より
$$|\,\alpha-\beta\,|\lt1\lt\alpha+\beta$$
$1\lt\alpha+\beta$ と②より
$$1\lt a \quad\cdots\text{④}$$
$|\,\alpha-\beta\,|\lt1$ の両辺は $0$ 以上なので、②より
$$\begin{align}
(\alpha-\beta)^2 &\lt 1 \\
(\alpha+\beta)^2-4\alpha\beta &\lt 1 \\
a^2-4b &\lt 1 \\
b &\gt \dfrac{1}{4}(a^2-1) \quad\cdots\text{⑤}
\end{align}$$
④,⑤より
$$b\gt\dfrac{1}{4}(a^2-1)\gt\dfrac{1}{4}(1^2-1)=0$$となるから③は満たされる。
したがって、①,④,⑤より、求める$(a,\,b)$ の範囲は
$$\boldsymbol{a\gt1},\quad\boldsymbol{\dfrac{1}{4}(a^2-1)\lt b\leqq\dfrac{1}{4}a^2}$$であり、これを図示すると下図の網掛け部分のようになる。ただし、境界は $\boldsymbol{a=1}$,$\boldsymbol{b=\dfrac{1}{4}(a^2-1)}$ を含まない。
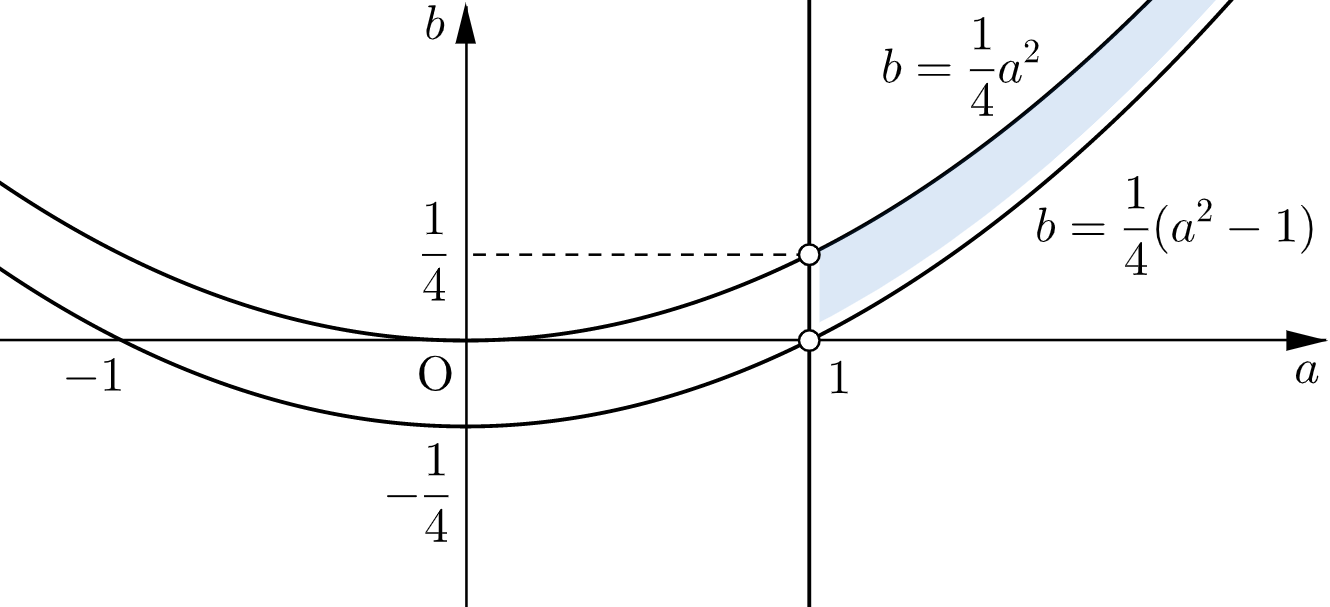
$$\boldsymbol{a\gt1},\quad\boldsymbol{\dfrac{1}{4}(a^2-1)\lt b\leqq\dfrac{1}{4}a^2}$$
領域は下図の網掛け部分(境界は $\boldsymbol{a=1}$,$\boldsymbol{b=\dfrac{1}{4}(a^2-1)}$ を含まない)

⑵
②より
$$\dfrac{\alpha\beta+1}{(\alpha+\beta)^2}=\dfrac{b+1}{a^2}$$であり
$$\dfrac{b+1}{a^2}=k$$とおくと、$b\gt0$ より $k\gt0$ であるから
$$b=ka^2-1 \quad\cdots\text{⑥}$$は $ab$ 平面上で $b$ 軸を軸とし $b$ 切片が $-1$ である下に凸の放物線を表す。
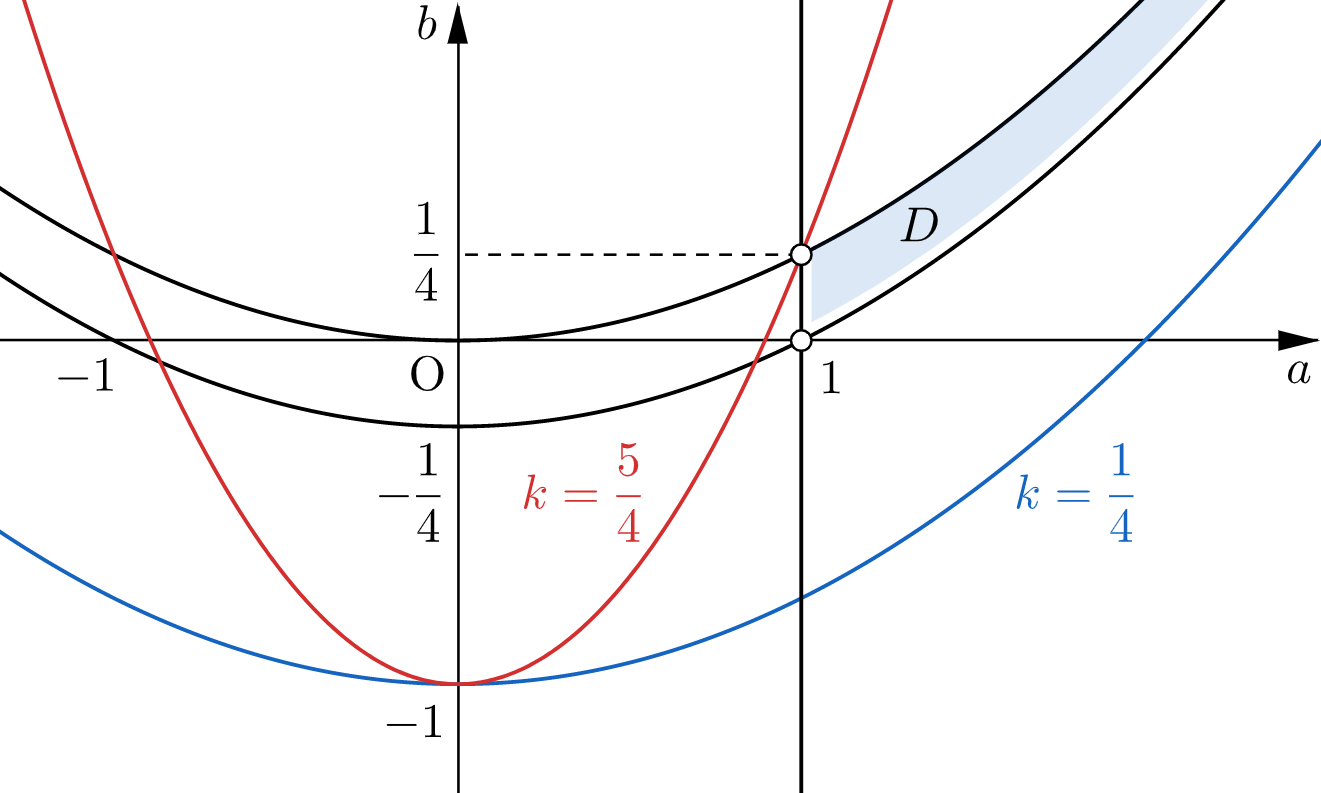
⑴で求めた領域を $D$ とすると、求める値の範囲は $D$ と放物線⑥が共有点をもつときに $k$ がとりうる値の範囲である。
$D$ と放物線⑥が共有点をもつことは、放物線 $b=\dfrac{1}{4}a^2$ の $a\gt1$ の部分と放物線⑥が共有点をもつことと同値である。
$2$ つの放物線の式から $b$ を消去すると
$$\begin{align}
ka^2-1 &= \dfrac{1}{4}a^2 \\
\therefore \ \left(k-\dfrac{1}{4}\right)a^2 &= 1 \quad\cdots\text{⑦}
\end{align}$$$(\text{左辺})\gt0$ となるためには
$$k\gt\dfrac{1}{4} \quad\cdots\text{⑧}$$が必要であり、このとき⑦の両辺を $k-\dfrac{1}{4}$ で除すと
$$\begin{align}
a^2=\dfrac{1}{k-\dfrac{1}{4}} &\gt 1 \ \text{(}\because a\gt1\,\text{)} \\
k-\dfrac{1}{4} &\lt 1 \\
k &\lt \dfrac{5}{4} \quad\cdots\text{⑨}
\end{align}$$
⑧,⑨より
$$\dfrac{1}{4}\lt k\lt\dfrac{5}{4}$$となるので、求める値の範囲は
$$\boldsymbol{\dfrac{1}{4}\lt\dfrac{\alpha\beta+1}{(\alpha+\beta)^2}\lt\dfrac{5}{4}}$$
$$\boldsymbol{\dfrac{1}{4}\lt\dfrac{\alpha\beta+1}{(\alpha+\beta)^2}\lt\dfrac{5}{4}}$$
解説
⑴は、三角形の成立条件を正しく同値変形しましょう。
この手の問題は $(\text{判別式})\gt0$ を忘れがちなので要注意です。
⑵は、範囲が知りたい値をまるごと $k$ とおいて、曲線と領域が共有点をもつときの $k$ の範囲を求める、という定番の問題です。
本解答では厳密に $k$ の範囲を求めましたが、図を用いてより簡略化した解答も良いと思います。
具体的には、$k$ は放物線⑥の「開き具合」を表し、$k=\dfrac{1}{4}$ のとき $b=\dfrac{1}{4}a^2$ と合同となり、$k=\dfrac{5}{4}$ のとき点 $\left(1,\dfrac{1}{4}\right)$ を通るので $\dfrac{1}{4}\lt k\lt\dfrac{5}{4}$ が得られる、という解答です。
曲線と領域が共有点をもつ条件を考えたんだな、ということが伝われば大丈夫です。
まとめ
今回は、一橋大学数学(2021年 第3問)の解説をしました。
ほかの問題にもチャレンジしよう!
一橋大学 数学 2021年 第1問 解説
一橋大学 数学 2021年 第2問 解説
一橋大学 数学 2021年 第3問 解説
一橋大学 数学 2021年 第4問 解説
一橋大学 数学 2021年 第5問 解説













