神戸大学 理系数学 2019年[後期] 第5問 解説

今回は、神戸大学理系数学（2019年後期 第5問）の解説をしたいと思います。

問題

$2$ つの科目 $\mathrm{X}$ と $\mathrm{Y}$ の試験を受けた $3$ 人の生徒の得点と，それぞれの科目の得点の平均値と標準偏差を以下のとおりとする．

ただし，$s_x\ne0$ かつ $s_y\ne0$ とする．科目 $\mathrm{X}$ と科目 $\mathrm{Y}$ の得点の相関係数 $r$ は
$$r=\dfrac{\displaystyle\sum_{i=1}^{3}(x_i-\overline{x})(y_i-\overline{y})}{\sqrt{\displaystyle\sum_{i=1}^{3}(x_i-\overline{x})^2}\sqrt{\displaystyle\sum_{i=1}^{3}(y_i-\overline{y})^2}}$$で与えられる．

　座標空間内に $3$ 点 $\mathrm{O}(0,0,0), \ $$\mathrm{A}(x_1,x_2,x_3), \ $$\mathrm{B}(y_1,y_2,y_3)$ をとる．$\mathrm{O}$ を通り，方向ベクトルが $(1,1,1)$ の直線を $\ell$ とする．$\ell$ 上の点 $\mathrm{P}$ を $\overrightarrow{\mathrm{PA}}$ と $\ell$ が垂直になるようにとり，$\ell$ 上の点 $\mathrm{Q}$ を $\overrightarrow{\mathrm{QB}}$ と $\ell$ が垂直になるようにとる．以下の問に答えよ．

⑴　点 $\mathrm{P}$，点 $\mathrm{Q}$ の座標と内積 $\overrightarrow{\mathrm{PA}}\cdot\overrightarrow{\mathrm{QB}}$ を $\overline{x}, \ $$\overline{y}, \ $$s_x, \ $$s_y, \ $$r$ を用いて表せ．

⑵　$a=\dfrac{|\overline{x}-\overline{y}|}{s_y}$ とおくとき，$\cos\angle\mathrm{BPA}$ を $a$ と $r$ を用いて表せ．

⑶　点 $\mathrm{A}$ と直線 $\ell$ を含む平面を $\alpha$ とする．平面 $\alpha$ 上の点 $\mathrm{C}$ を $\overrightarrow{\mathrm{PC}}=\overrightarrow{\mathrm{PA}}+\overrightarrow{\mathrm{PQ}}$ となるようにとる．点 $\mathrm{B}$ は $\alpha$ 上にないとし，$\alpha$ 上の点 $\mathrm{K}$ を $\overrightarrow{\mathrm{KB}}$ と $\alpha$ が垂直になるようにとる．科目 $\mathrm{X}$ と科目 $\mathrm{Y}$ の得点の相関係数 $r$ が $0\lt r\lt\dfrac{s_x}{s_y}$ をみたすとき，点 $\mathrm{K}$ は線分 $\mathrm{QC}$ 上にあることを示せ．

（神戸大学）

解答

⑴

点 $\mathrm{P}$ は直線 $\ell$ 上の点なので、実数 $k$ を用いて
$$\overrightarrow{\mathrm{OP}}=k(1,1,1)=(k,k,k)$$と表せ、$\overrightarrow{\mathrm{PA}}\perp\ell$ より
$$\begin{array}{c}\begin{aligned}
(k-x_1,\,k-x_2,\,k-x_3)\cdot(1,1,1) &= 0 \\[0.2em]
k-x_1+k-x_2+k-x_3 &= 0
\end{aligned} \\[0.3em]
\therefore \ k=\dfrac{x_1+x_2+x_3}{3}=\overline{x}
\end{array}$$となるから、点 $\mathrm{P}$ の座標は $\boldsymbol{(\overline{x},\,\overline{x},\,\overline{x})}$ である。

同様に、点 $\mathrm{Q}$ の座標は $\boldsymbol{(\overline{y},\,\overline{y},\,\overline{y})}$ である。

したがって
$$\begin{align}
\overrightarrow{\mathrm{PA}}\cdot\overrightarrow{\mathrm{QB}} &= \begin{pmatrix}x_1-\overline{x} \\ x_2-\overline{x} \\ x_3-\overline{x}\end{pmatrix}\cdot\begin{pmatrix}y_1-\overline{y} \\ y_2-\overline{y} \\ y_3-\overline{y}\end{pmatrix} \\
&= \displaystyle\sum_{i=1}^{3}(x_i-\overline{x})(y_i-\overline{y}) \\
&= r\sqrt{\displaystyle\sum_{i=1}^{3}(x_i-\overline{x})^2}\sqrt{\displaystyle\sum_{i=1}^{3}(y_i-\overline{y})^2} \\
&= 3r\sqrt{\dfrac{1}{3}\displaystyle\sum_{i=1}^{3}(x_i-\overline{x})^2}\sqrt{\dfrac{1}{3}\displaystyle\sum_{i=1}^{3}(y_i-\overline{y})^2} \\
&= \boldsymbol{3rs_xs_y}
\end{align}$$

⑵

$\overrightarrow{\mathrm{PA}}\perp\overrightarrow{\mathrm{PQ}}, \ $$\overrightarrow{\mathrm{QB}}\perp\overrightarrow{\mathrm{PQ}}$ に注意すると
$$\begin{align}
\overrightarrow{\mathrm{PA}}\cdot\overrightarrow{\mathrm{PB}} &= \overrightarrow{\mathrm{PA}}\cdot(\overrightarrow{\mathrm{PQ}}+\overrightarrow{\mathrm{QB}}) \\
&= 0+\overrightarrow{\mathrm{PA}}\cdot\overrightarrow{\mathrm{QB}} \\
&= 3rs_xs_y, \\[0.7em]
|\overrightarrow{\mathrm{PA}}| &= \sqrt{\displaystyle\sum_{i=1}^{3}(x_i-\overline{x})^2}=\sqrt{3}s_x, \\[0.7em]
|\overrightarrow{\mathrm{PB}}| &= \sqrt{|\overrightarrow{\mathrm{PQ}}|^2+|\overrightarrow{\mathrm{QB}}|^2} \\
&= \sqrt{3(\overline{x}-\overline{y})^2+\displaystyle\sum_{i=1}^{3}(y_i-\overline{y})^2} \\
&= \sqrt{3a^2s_y^{\,2}+3s_y^{\,2}} \\
&= \sqrt{3s_y^{\,2}(a^2+1)} \\
&= \sqrt{3}s_y\sqrt{a^2+1} \ \text{（}\because s_y\gt 0 \ \text{）}
\end{align}$$であるから$$\begin{align}
\cos\angle\mathrm{BPA} &= \dfrac{\overrightarrow{\mathrm{PA}}\cdot\overrightarrow{\mathrm{PB}}}{|\overrightarrow{\mathrm{PA}}||\overrightarrow{\mathrm{PB}}|} \\
&= \dfrac{3rs_xs_y}{\sqrt{3}s_x\cdot\sqrt{3}s_y\sqrt{a^2+1}} \\
&= \boldsymbol{\dfrac{r}{\sqrt{a^2+1}}}
\end{align}$$

⑶

$\overrightarrow{\mathrm{PA}}\perp\overrightarrow{\mathrm{PQ}}$ より $\overrightarrow{\mathrm{QC}}=\overrightarrow{\mathrm{PA}}, \ $$\overrightarrow{\mathrm{QC}}\perp\overrightarrow{\mathrm{PQ}}$ である。

また、$\alpha$ は $\overrightarrow{\mathrm{PQ}}, \ $$\overrightarrow{\mathrm{QC}}$ を含む平面であり、$\overrightarrow{\mathrm{QB}}\perp\overrightarrow{\mathrm{PQ}}$ より、点 $\mathrm{K}$ は直線 $\mathrm{QC}$ 上に存在する。

ここで、平面 $\alpha$ 上の点 $\mathrm{D}$ を $\overrightarrow{\mathrm{QD}}=\overrightarrow{\mathrm{QP}}+\overrightarrow{\mathrm{QK}}$ となるようにとると、$\overrightarrow{\mathrm{QP}}\perp\overrightarrow{\mathrm{QK}}$ より $\overrightarrow{\mathrm{QK}}=\overrightarrow{\mathrm{PD}}$ となる。

$\mathrm{QK}/\!/\mathrm{PA}$ より点 $\mathrm{D}$ は直線 $\mathrm{PA}$ 上に存在し、$\overrightarrow{\mathrm{PD}}\perp\overrightarrow{\mathrm{KD}}$ より $\overrightarrow{\mathrm{PD}}\perp\overrightarrow{\mathrm{BD}}$ である。

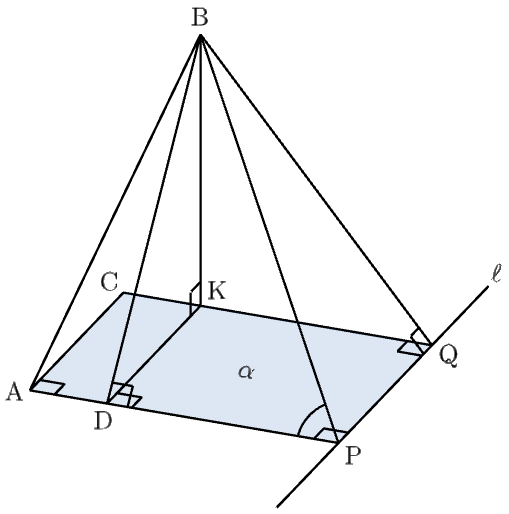
よって
$$\begin{align}
\overrightarrow{\mathrm{QK}} &= \overrightarrow{\mathrm{PD}}=\dfrac{|\overrightarrow{\mathrm{PD}}|}{|\overrightarrow{\mathrm{PA}}|}\overrightarrow{\mathrm{PA}} \\
&= \dfrac{|\overrightarrow{\mathrm{PB}}|\cos\angle\mathrm{BPA}}{|\overrightarrow{\mathrm{PA}}|}\overrightarrow{\mathrm{PA}} \\
&= \dfrac{|\overrightarrow{\mathrm{PB}}|}{|\overrightarrow{\mathrm{PA}}|}\cdot\dfrac{\overrightarrow{\mathrm{PA}}\cdot\overrightarrow{\mathrm{PB}}}{|\overrightarrow{\mathrm{PA}}||\overrightarrow{\mathrm{PB}}|}\overrightarrow{\mathrm{PA}} \\
&= \dfrac{\overrightarrow{\mathrm{PA}}\cdot\overrightarrow{\mathrm{PB}}}{|\overrightarrow{\mathrm{PA}}|^2}\overrightarrow{\mathrm{PA}} \\
&= \dfrac{3rs_xs_y}{3s_x^2}\overrightarrow{\mathrm{PA}} \ \text{（}\because\text{⑵）} \\
&= \dfrac{rs_y}{s_x}\overrightarrow{\mathrm{PA}} \\[0.3em]
\therefore \ \overrightarrow{\mathrm{QK}} &= \dfrac{rs_y}{s_x}\overrightarrow{\mathrm{QC}}
\end{align}$$

条件より $0\lt r\lt\dfrac{s_x}{s_y}$ であり、$s_x\gt0, \ $$s_y\gt0$ より $0\lt\dfrac{rs_y}{s_x}\lt1$ であるから、点 $\mathrm{K}$ は線分 $\mathrm{QC}$ 上にある。$$\tag{証明終}$$

解説

「データの分析」と「ベクトル」を融合させたユニークな問題で多少面食らいますが、与えられた条件を丁寧に処理していけば大丈夫です。

⑶は、点 $\mathrm{K}$ の座標を具体的に求める方法もありますが、記述がとても複雑になるので、本解答では垂直の性質を活かして点の存在位置を絞りました。

まとめ

今回は、神戸大学理系数学（2019年後期 第5問）の解説をしました。