神戸大学 理系数学 2019年[後期] 第2問 解説

今回は、神戸大学理系数学（2019年後期 第2問）の解説をしたいと思います。

問題

連立不等式
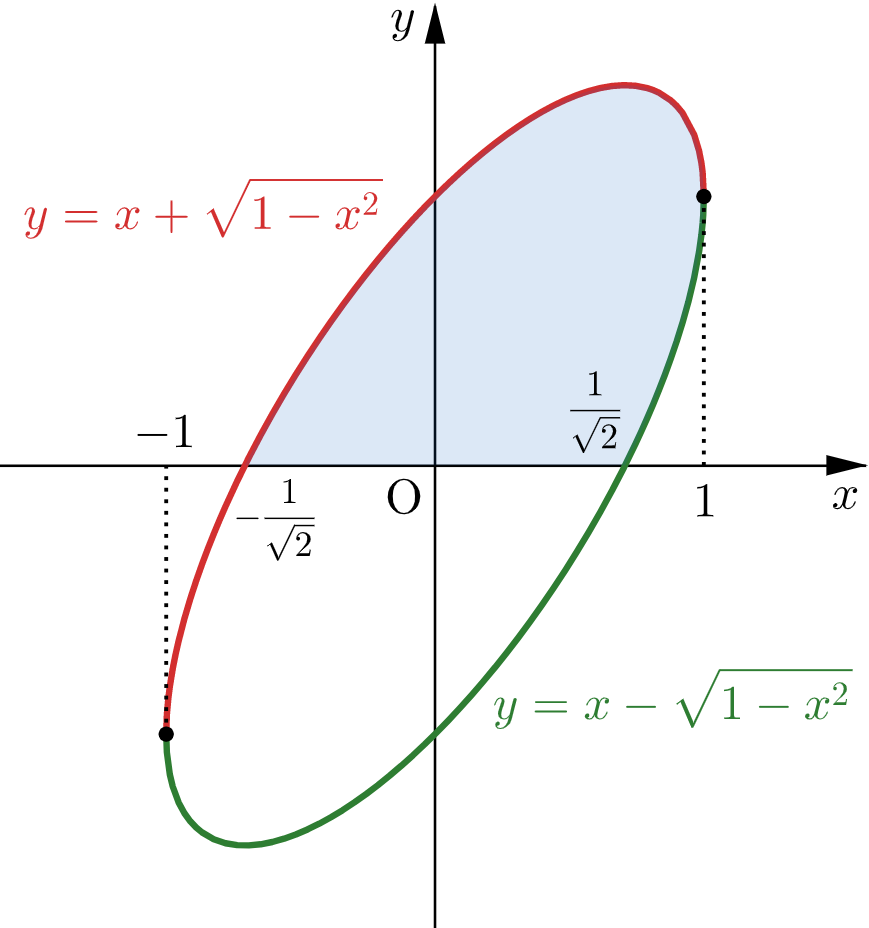
$$y\geqq 0,\quad y^2-2xy+2x^2-1\leqq 0$$が表す $xy$ 平面上の領域を $x$ 軸のまわりに $1$ 回転してできる立体を $D$ とする．以下の問に答えよ．

⑴　不等式 $x-\sqrt{1-x^2}\geqq 0$ を解け．

⑵　不等式 $x+\sqrt{1-x^2}\geqq 0$ を解け．

⑶　$t$ を $-1\leqq t\leqq 1$ をみたす実数とする．$xy$ 平面上の点 $(t,0)$ を通り $x$ 軸と垂直な平面による $D$ の切り口の面積 $S(t)$ を求めよ．ただし，この平面と $D$ の共通部分がない場合は $S(t)=0$ とする．

⑷　$D$ の体積 $V$ を求めよ．

（神戸大学）

解答

⑴

$x-\sqrt{1-x^2}\geqq 0$ より
$$x\geqq\sqrt{1-x^2} \ \ (\geqq 0) \quad\cdots(*)$$

$0\leqq x\leqq 1$ のとき $(*)$ の両辺は $0$ 以上なので、両辺を $2$ 乗して
$$\begin{array}{c}
x^2 \geqq 1-x^2 \\[0.3em]
\therefore \ x\leqq-\dfrac{1}{\sqrt{2}}, \ \dfrac{1}{\sqrt{2}}\leqq x
\end{array}$$$0\leqq x\leqq 1$ より
$$\boldsymbol{\dfrac{1}{\sqrt{2}}\leqq x\leqq 1}$$

⑵

$x+\sqrt{1-x^2}\geqq 0$ より
$$\sqrt{1-x^2}\geqq-x\quad\cdots(**)$$

$\sqrt{1-x^2}\geqq 0$ より $-1\leqq x\leqq 1$ が必要である。

(ⅰ)　$0\leqq x\leqq 1$ のとき
$$\sqrt{1-x^2}\geqq 0,\quad -x\leqq 0$$より $(**)$ は常に成り立つ。

(ⅱ)　$-1\leqq x\lt 0$ のとき
$(**)$ の両辺は $0$ 以上なので、両辺を $2$ 乗して
$$\begin{array}{c}
1-x^2 \geqq x^2 \\[0.3em]
\therefore \ -\dfrac{1}{\sqrt{2}}\leqq x\leqq\dfrac{1}{\sqrt{2}}
\end{array}$$$-1\leqq x\lt 0$ より
$$-\dfrac{1}{\sqrt{2}}\leqq x\lt 0$$

(ⅰ),(ⅱ)より、求める解は
$$\boldsymbol{-\dfrac{1}{\sqrt{2}}\leqq x\leqq 1}$$

⑶

$y^2-2xy+2x^2-1\leqq 0$ より
$$\begin{array}{c}
\left\{y-\left(x-\sqrt{1-x^2}\right)\right\}\left\{y-\left(x+\sqrt{1-x^2}\right)\right\}\leqq 0 \\[0.3em]
x-\sqrt{1-x^2}\leqq y\leqq x+\sqrt{1-x^2}
\end{array}$$

(ⅰ),(ⅱ)および $y\geqq 0$ より、$-1\leqq t\leqq 1$ における平面 $x=t$ と $D$ の共通部分は
$$\left\{
\begin{array}{ll}
\text{存在しない} & \left(-1\leqq t\lt-\dfrac{1}{\sqrt{2}} \ \text{のとき}\right) \\
0\leqq y\leqq x+\sqrt{1-x^2} & \left(-\dfrac{1}{\sqrt{2}}\leqq t\leqq\dfrac{1}{\sqrt{2}} \ \text{のとき}\right) \\
x-\sqrt{1-x^2}\leqq y\leqq x+\sqrt{1-x^2} & \left(\dfrac{1}{\sqrt{2}}\lt t\leqq1 \ \text{のとき}\right) \\
\end{array}
\right.$$となる。

$-\dfrac{1}{\sqrt{2}}\leqq t\leqq\dfrac{1}{\sqrt{2}}$ のとき
$$\begin{align}
S(t) &= \pi\left(t+\sqrt{1-t^2}\right)^2 \\
&= \pi\left(1+2t\sqrt{1-t^2}\right)
\end{align}$$

$\dfrac{1}{\sqrt{2}}\lt t\leqq1$ のとき
$$\begin{align}
S(t) &= \pi\left(t+\sqrt{1-t^2}\right)^2-\pi\left(t-\sqrt{1-t^2}\right)^2 \\
&= 4\pi t\sqrt{1-t^2}
\end{align}$$

以上より
$$S(t)=\left\{
\begin{array}{ll}
\mathbf{0} & \left(\boldsymbol{-1\leqq t\lt-\dfrac{1}{\sqrt{2}}} \ \mathbf{\text{のとき}}\right) \\
\boldsymbol{\pi\left(1+2t\sqrt{1-t^2}\right)} & \left(\boldsymbol{-\dfrac{1}{\sqrt{2}}\leqq t\leqq\dfrac{1}{\sqrt{2}}} \ \mathbf{\text{のとき}}\right) \\
\boldsymbol{4\pi t\sqrt{1-t^2}} & \left(\boldsymbol{\dfrac{1}{\sqrt{2}}\lt t\leqq1} \ \mathbf{\text{のとき}}\right) \\
\end{array}
\right.$$

⑷

$t\sqrt{1-t^2}$ が奇関数であることに注意すると、⑶より
$$\begin{align}
V &= \displaystyle\int_{-1}^{1}S(t)dt \\
&= \displaystyle\int_{-\frac{1}{\sqrt{2}}}^{\frac{1}{\sqrt{2}}}\pi\left(1+2t\sqrt{1-t^2}\right)dt+\displaystyle\int_{\frac{1}{\sqrt{2}}}^{1}4\pi t\sqrt{1-t^2}dt \\
&= 2\pi\displaystyle\int_{0}^{\frac{1}{\sqrt{2}}}dt+4\pi\displaystyle\int_{\frac{1}{\sqrt{2}}}^{1}t\sqrt{1-t^2}dt \\
&= 2\pi\Big[ \ x \ \Big]_{0}^{\frac{1}{\sqrt{2}}}+4\pi\left[-\dfrac{1}{3}\left(1-t^2\right)^{\frac{3}{2}}\right]_{\frac{1}{\sqrt{2}}}^{1} \\
&= \sqrt{2}\pi+\dfrac{4}{3}\cdot\left(\dfrac{1}{2}\right)^{\frac{3}{2}} \\
&= \boldsymbol{\dfrac{4\sqrt{2}}{3}\pi}
\end{align}$$

解説

⑴,⑵を⑶でどう活かすかがポイントです。

誘導が丁寧なので、⑷は積分を計算するだけですが、積分区間が $0$ に関して対称なときは奇関数・偶関数がないか確認しましょう。
計算量と計算ミスを減らすことができます。

まとめ

今回は、神戸大学理系数学（2019年後期 第2問）の解説をしました。