京都大学 理学部特色入試（数学）2021年度 第1問 解説

今回は、京都大学理学部特色入試・数学（2021年度 第1問）の解説をしたいと思います。

問題

　$n$ を $3$ 以上の自然数，$\lambda$ を実数とする．次の条件(ⅰ)，(ⅱ)を満たす空間ベクトル $\overrightarrow{v_1},\overrightarrow{v_2},\dots,\overrightarrow{v_n}$ が存在するための，$n$ と $\lambda$ が満たすべき条件を求めよ．

(ⅰ)　$\overrightarrow{v_1},\overrightarrow{v_2},\dots,\overrightarrow{v_n}$ は相異なる長さ $1$ の空間ベクトルである．

(ⅱ)　$i \ne j$ のときベクトル $\overrightarrow{v_i}$ と $\overrightarrow{v_i}$ の内積は $\lambda$ に等しい．

（京都大学）

解答

$i \ne j$ のとき、$\overrightarrow{v_i}$ と $\overrightarrow{v_j}$ のなす角を $\theta_{ij}$（ $0\leqq\theta_{ij}\leqq\pi$ ）とおくと
$$\begin{align}
\lambda &= \overrightarrow{v_i} \cdot \overrightarrow{v_j} \\
&= |\overrightarrow{v_i}||\overrightarrow{v_j}|\cos\theta_{ij} \\
&= 1 \cdot 1 \cdot \cos\theta_{ij} \\
&= \cos\theta_{ij}
\end{align}$$となる。$0\leqq\theta_{ij}\leqq\pi$ の範囲において $\theta_{ij}$ と $\cos\theta_{ij}$ は $1$ 対 $1$ 対応するので、条件(ⅱ)は
「 $i \ne j$ のとき、$\overrightarrow{v_i}$ と $\overrightarrow{v_j}$ のなす角は $\theta_{ij}$ で一定である。」
と同値である。以下、$\theta_{ij}$ を単に $\theta$ と表す。

また、$i \ne j$ のとき
$$\begin{align}
|\overrightarrow{v_i} \cdot \overrightarrow{v_j}| &= |\overrightarrow{v_i}||\overrightarrow{v_j}||\cos\theta| \\
&\leqq |\overrightarrow{v_i}||\overrightarrow{v_j}| \\
&= 1 \cdot 1 =1
\end{align}$$より、$|\lambda| \leqq 1$ となる。

$\lambda=1$ のとき、$\cos\theta=1$ すなわち $\theta=0$ となるが、これを満たす相異なる長さ $1$ の空間ベクトルは $2$ 本以上とれない。よって、$\lambda \ne 1$ である。

また $\lambda = -1$ のとき、$\cos\theta=-1$ すなわち $\theta=\pi$ となるが、これを満たす相異なる長さ $1$ の空間ベクトルは $3$ 本以上とれない。よって、$\lambda \ne -1$ である。

したがって、以下、$-1 \lt \lambda \lt 1, \ $$0\lt\theta\lt\pi$ とする。

ここで、$\mathrm{O}$ を原点とする $xyz$ 座標空間を考え、$\overrightarrow{v_1},\overrightarrow{v_2},\cdots,\overrightarrow{v_n}$ の始点を $\mathrm{O}$ におき、終点をそれぞれ $\mathrm{P}_1,\mathrm{P}_2,\cdots,\mathrm{P}_n$ とする。このとき、点 $\mathrm{P}_1,\mathrm{P}_2,\cdots,\mathrm{P}_n$ は原点を中心とする半径 $1$ の球面上に位置している。

$$\overrightarrow{\mathrm{OP}_1}=\overrightarrow{v_1}=
\begin{pmatrix}1 \\ 0 \\ 0\end{pmatrix},
\quad
\overrightarrow{\mathrm{OP}_2}=\overrightarrow{v_2}=
\begin{pmatrix}\cos\theta \\ \sin\theta \\ 0\end{pmatrix}$$としても一般性を失わない。

(ア)　$n=3$ のとき

$\overrightarrow{v_1},\overrightarrow{v_2}$ に加え、条件(ⅰ),(ⅱ)を満たすように $3$ 本目のベクトル $\overrightarrow{v_3}$ をとることを考えると、その終点 $\mathrm{P}_3$ は、「直線 $\mathrm{OP}_1$（ $x$ 軸）を中心軸として点 $\mathrm{P}_2$ を $1$ 回転させたときの軌跡（ただし $\mathrm{P}_2$ を除く。）」にある。この軌跡を $C$ とする。

ここで、点 $\mathrm{P}_2$ から直線 $\mathrm{OP}_1$ に下ろした垂線の足を $\mathrm{Q}$ とし、平面 $x=\cos\theta$ 上において $\overrightarrow{\mathrm{QP}_2}$ から反時計回りに測った $\overrightarrow{\mathrm{QP}_3}$ の角度を $\varphi$ とする。$\mathrm{P}_3$ は $\mathrm{P}_2$ と異なる点なので、$\varphi$ の範囲は $0 \lt \varphi \lt 2\pi$ である。

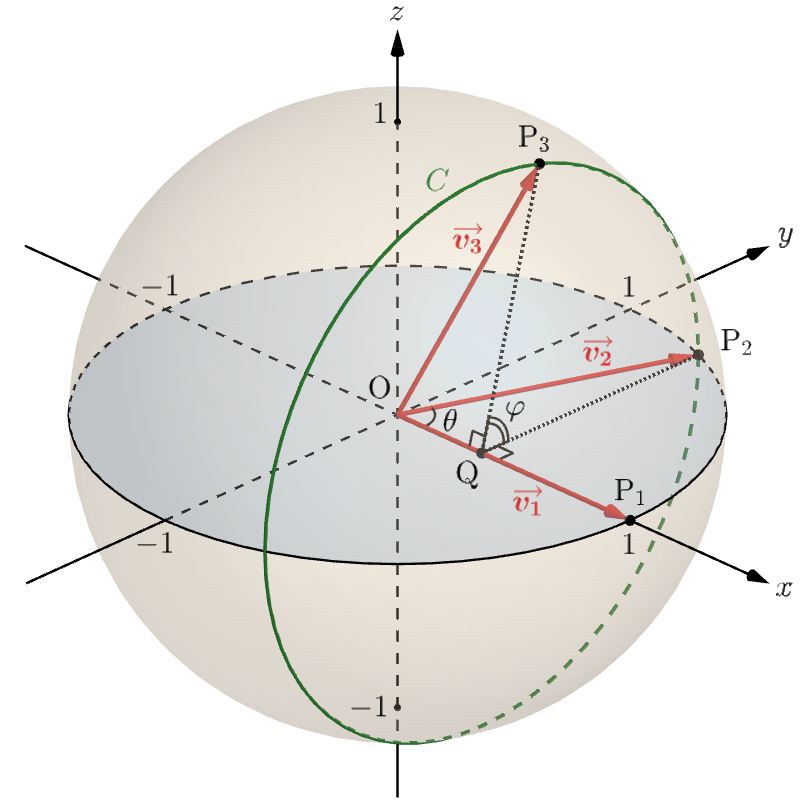
このとき
$$\overrightarrow{\mathrm{OP}_3}=\overrightarrow{v_3}=
\begin{pmatrix}\cos\theta \\ \sin\theta\cos\varphi \\ \sin\theta\sin\varphi\end{pmatrix}$$とおける。

条件(ⅱ)より、$\overrightarrow{v_2} \cdot \overrightarrow{v_3} = \cos\theta$ なので
$$\begin{align}
\begin{pmatrix}\cos\theta \\ \sin\theta \\ 0\end{pmatrix} \cdot
\begin{pmatrix}\cos\theta \\ \sin\theta\cos\varphi \\ \sin\theta\sin\varphi\end{pmatrix} &= \cos\theta \\
\cos^2\theta + \sin^2\theta\cos\varphi &= \cos\theta
\end{align}$$$0\lt\theta\lt\pi$ より $\sin^2\theta \ne 0$ なので
$$\begin{align}
\cos\varphi &= \dfrac{\cos\theta-\cos^2\theta}{\sin^2\theta} \\
&= \dfrac{\cos\theta(1-\cos\theta)}{(1+\cos\theta)(1-\cos\theta)} \\[0.5em]
\therefore \ \cos\varphi&= \dfrac{\cos\theta}{1+\cos\theta} \quad\cdots\text{①}
\end{align}$$

$0 \lt \varphi \lt 2\pi$ の範囲に $\varphi$ が存在するとき、$-1 \leqq \cos\varphi \lt 1$ であるから
$$-1 \leqq \dfrac{\cos\theta}{1+\cos\theta} \lt 1$$$1+\cos\theta \gt 0$ より
$$\begin{eqnarray}
-1-\cos\theta &\leqq& \cos\theta \lt 1+\cos\theta \\
\therefore \ -\dfrac{1}{2} &\leqq& \cos\theta \lt 1 \quad\cdots\text{②}
\end{eqnarray}$$

逆に $\cos\theta$ が②の範囲にあるとき、①を満たす $\varphi$ が存在し、それは $\mathrm{P}_3$（ $\overrightarrow{v_3}$ ）がとれることと同値である。

よって、$n=3$ のとき、$\lambda$ が満たすべき条件は $-\dfrac{1}{2} \leqq \lambda \lt 1$ である。

(イ)　$n=4$ のとき

$\overrightarrow{v_1},\overrightarrow{v_2},\overrightarrow{v_3}$ に加え、条件(ⅰ),(ⅱ)を満たすように $4$ 本目のベクトル $\overrightarrow{v_4}$ をとることを考えると、その終点 $\mathrm{P}_4$ は、$\mathrm{P}_3$ と同様に軌跡 $C$ 上にあるので、$0 \lt \varphi’ \lt 2\pi$ を満たす $\varphi’$ を用いて
$$\overrightarrow{\mathrm{OP}_4}=\overrightarrow{v_4}=
\begin{pmatrix}\cos\theta \\ \sin\theta\cos\varphi’ \\ \sin\theta\sin\varphi’\end{pmatrix}$$とおける。

(ア)と同様の議論により、$\cos\theta$ が②の範囲にあるとき、
$$\cos\varphi’ = \dfrac{\cos\theta}{1+\cos\theta}$$を満たす $\varphi’$ が存在し、このとき、$\cos\varphi’ = \cos\varphi$ である。$\mathrm{P}_4$ は $\mathrm{P}_3$ と異なるので、$\varphi’ \ne \varphi$ であるから
$$\varphi’ = 2\pi \ – \ \varphi$$となる。

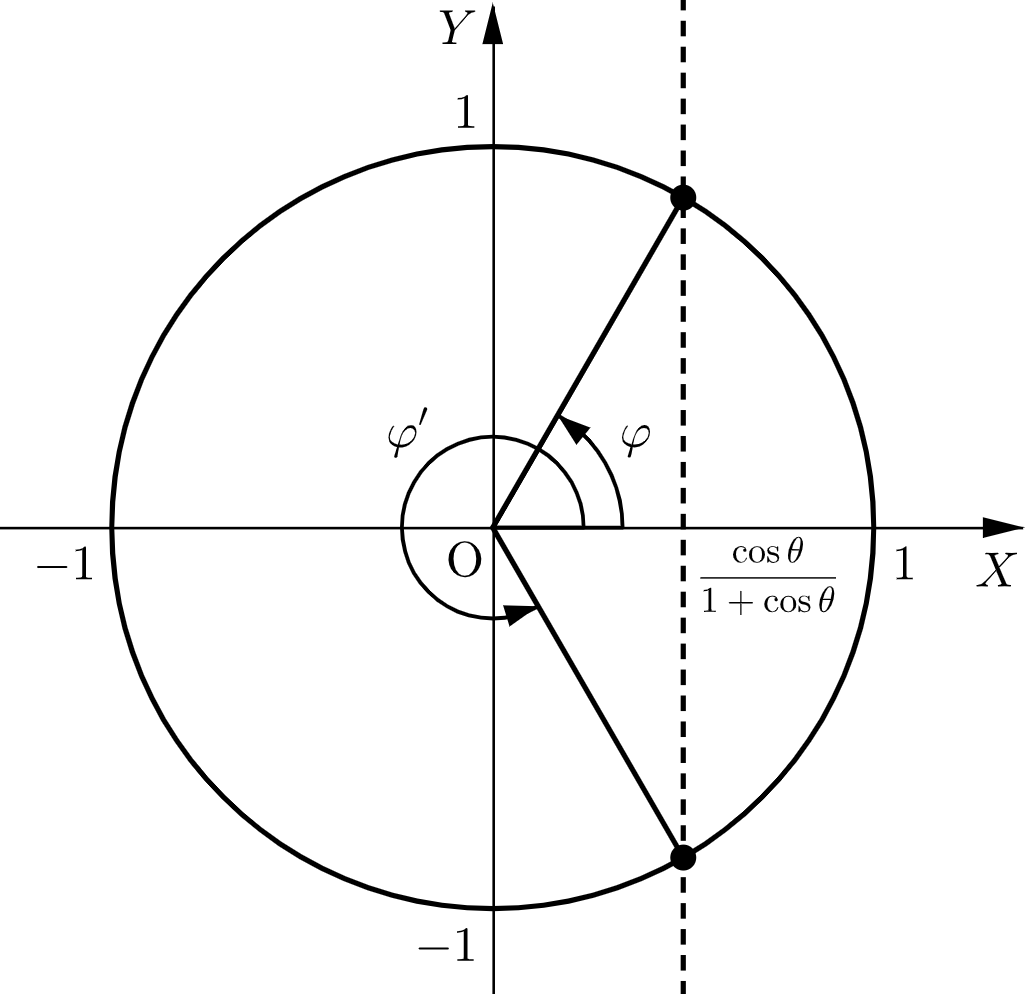
条件(ⅱ)より、$\overrightarrow{v_3} \cdot \overrightarrow{v_4} = \cos\theta$ なので
$$\begin{array}{c}
\begin{aligned}
\begin{pmatrix}\cos\theta \\ \sin\theta\cos\varphi \\ \sin\theta\sin\varphi\end{pmatrix} \cdot
\begin{pmatrix}\cos\theta \\ \sin\theta\cos\varphi’ \\ \sin\theta\sin\varphi’\end{pmatrix} &= \cos\theta \\
\begin{pmatrix}\cos\theta \\ \sin\theta\cos\varphi \\ \sin\theta\sin\varphi\end{pmatrix} \cdot
\begin{pmatrix}\cos\theta \\ \sin\theta\cos\varphi \\ \sin\theta(-\sin\varphi)\end{pmatrix} &= \cos\theta \\[0.5em]
\cos^2\theta + \sin^2\theta\cos^2\varphi-\sin^2\theta\sin^2\varphi &= \cos\theta
\end{aligned} \\[0.3em]
\begin{aligned}
\cos\theta-\cos^2\theta &= \sin^2\theta ( \cos^2\varphi \ – \sin^2\varphi ) \\
&= \sin^2\theta (2\cos^2\varphi -1) \\
&= \sin^2\theta \left\{ 2 \cdot \dfrac{\cos^2\theta}{(1+\cos\theta)^2} -1 \right\}
\end{aligned}
\end{array}$$両辺に $(1+\cos\theta)^2$ をかけると
$$\begin{align}
(1+\cos\theta)^2(\cos\theta-\cos^2\theta) &= (1-\cos^2\theta)\{ 2\cos^2\theta-(1+\cos\theta)^2 \} \\
(1+\cos\theta)^2 \cos\theta (1-\cos\theta) &= (1+\cos\theta)(1-\cos\theta)(\cos^2\theta-2\cos\theta-1)
\end{align}$$$0\lt\theta\lt\pi$ より $1-\cos\theta \ne 0$ なので
$$\begin{array}{c}
\begin{aligned}
(1+\cos\theta)^2 \cos\theta &= (1+\cos\theta)(\cos^2\theta-2\cos\theta-1) \\
\cos\theta+2\cos^2\theta+\cos^3\theta &= \cos^3\theta-\cos^2\theta-\cos\theta-1\end{aligned} \\
\begin{aligned}
3\cos^2\theta+4\cos\theta+1 &= 0 \\
(3\cos\theta+1)(\cos\theta+1) &= 0
\end{aligned}
\end{array}$$$0\lt\theta\lt\pi$ より $\cos\theta=-\dfrac{1}{3}$ となる。

逆にこのとき、条件を満たす $\mathrm{P}_4$（ $\overrightarrow{v_4}$ ）がとれる。

よって、$n=4$ のとき、$\lambda$ が満たすべき条件は $\lambda=-\dfrac{1}{3}$ である。

(ウ)　$n \geqq 5$ のとき

$\overrightarrow{v_1},\overrightarrow{v_2},\overrightarrow{v_3},\overrightarrow{v_4}$ に加え、条件(ⅰ),(ⅱ)を満たすように $5$ 本目のベクトル $\overrightarrow{v_5}$ をとることを考えると、(ア),(イ)と同様の議論により
$$\cos\alpha = \dfrac{\cos\theta}{1+\cos\theta}$$を満たす $\alpha$（ $0 \lt \alpha \lt 2\pi$ ）が存在する必要があるが、この解は $\alpha = \varphi,\varphi’$ のみなので、$\mathrm{P}_3,\mathrm{P}_4$ のどちらとも異なる点 $\mathrm{P}_5$ をとることはできない。

したがって、条件を満たす $\overrightarrow{v_5}$ がとれないので、$n \geqq 5$ のとき、条件(ⅰ),(ⅱ)を満たす $\lambda$ は存在しない。

(ア)～(ウ)より、求める条件は、「 $\boldsymbol{n=3}$ かつ $\boldsymbol{ -\dfrac{1}{2} \leqq \lambda \lt 1 }$ 」または「 $\boldsymbol{ n=4 }$ かつ $\boldsymbol{ \lambda = -\dfrac{1}{3} }$ 」である。

解説

この問題は設定がシンプルなので、状況はすぐにつかめると思います。また、$n=3$ のときの $\lambda$ の範囲や、$n$ が大きくなると条件(ⅰ),(ⅱ)を両方満たすのは難しそうなことは推測できると思います。それをどう論理的に表現・式展開していくかが難しいところです。

本解答では、$n$ を大きくすると、満たさなければならない必要条件も増えていって、$n=5$ 以降で不適になる、といった方針で解きました。

$3$ 次元空間で角度のからむ問題のときは、解答のように $3$ 次元極座標を使うとラクに解けるものがあります。ただし、どこからどの向きに測った角度なのかを明記しましょう。

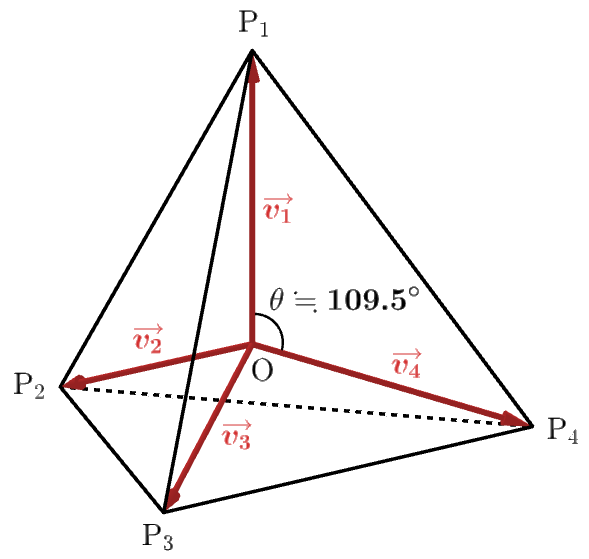
なお、$n=4, \ $$\lambda=-\dfrac{1}{3}$ のとき、下図のように $\mathrm{P}_1$ ～ $\mathrm{P}_4$ は正四面体の頂点に位置しています。

まとめ

今回は、京都大学理学部特色入試・数学（2021年度 第1問）の解説をしました。