一橋大学 数学 2022年[後期] 第3問 解説

今回は、一橋大学数学（2022年後期 第3問）の解説をしたいと思います。

問題

　$x,\,y$ を実数とするとき
$$\min(x-y^2, \ y-x^2)$$の最大値を求めよ。ただし，実数 $a,\,b$ に対して，$a\leqq b$ のとき $\min(a,\,b)=a$，$a\geqq b$ のとき $\min(a,\,b)=b$ とする。

（一橋大学）

解答

(ⅰ)　$\min(x-y^2, \ y-x^2)=y-x^2$ となるとき

$$\begin{align}
x-y^2 &\geqq y-x^2 \\[0.2em]
x^2-y^2+x-y &\geqq 0 \\[0.2em]
\therefore \ (x-y)(x+y+1) &\geqq 0
\end{align}$$となり、これは「$\,x-y\geqq0$ かつ $x+y+1\geqq0\,$」または「$\,x-y\leqq0$ かつ $x+y+1\leqq0\,$」すなわち「$\,y\leqq x$ かつ $y\geqq-x-1\,$」または「$\,y\geqq x$ かつ $y\leqq-x-1\,$」$\cdots\text{①}$ と同値である。

領域①を $xy$ 平面上に図示すると下図の網掛け部分のようになる。

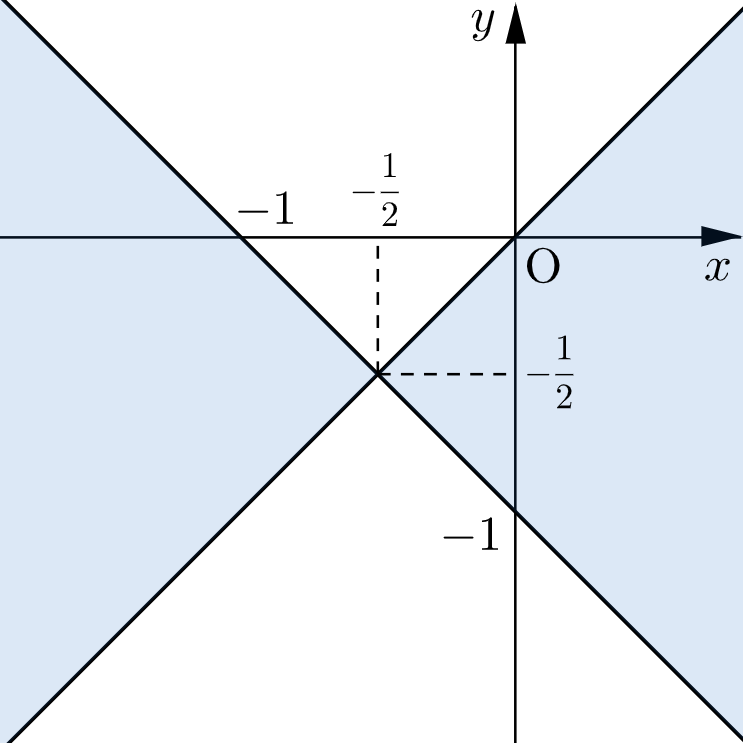
ここで
$$y-x^2=k \quad\cdots\text{②}$$とおくと、②は $y$ 軸を軸とし $y$ 切片が $k$ である放物線とみなせる。

すなわち、求める最大値は「領域①と放物線②が共有点をもつときの $k$ の最大値」である。

(ア)　放物線②が直線 $y=x$ と接するとき

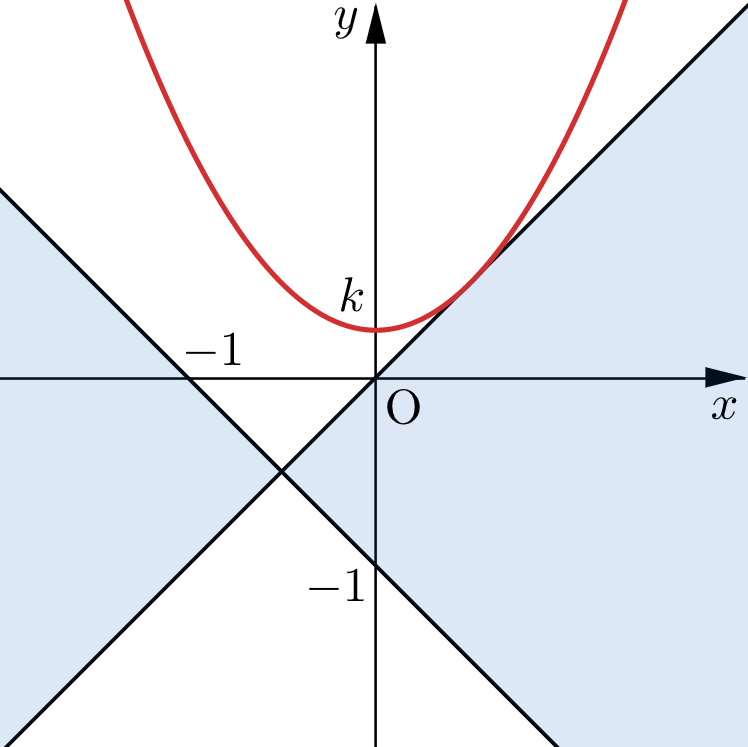
$x-x^2=k$ すなわち $x^2-x+k=0$ の判別式が $0$ となるので
$$1-4k=0 \ \Longleftrightarrow \ k=\dfrac{1}{4}$$

(イ)　放物線②が直線 $y=-x-1$ と接するとき

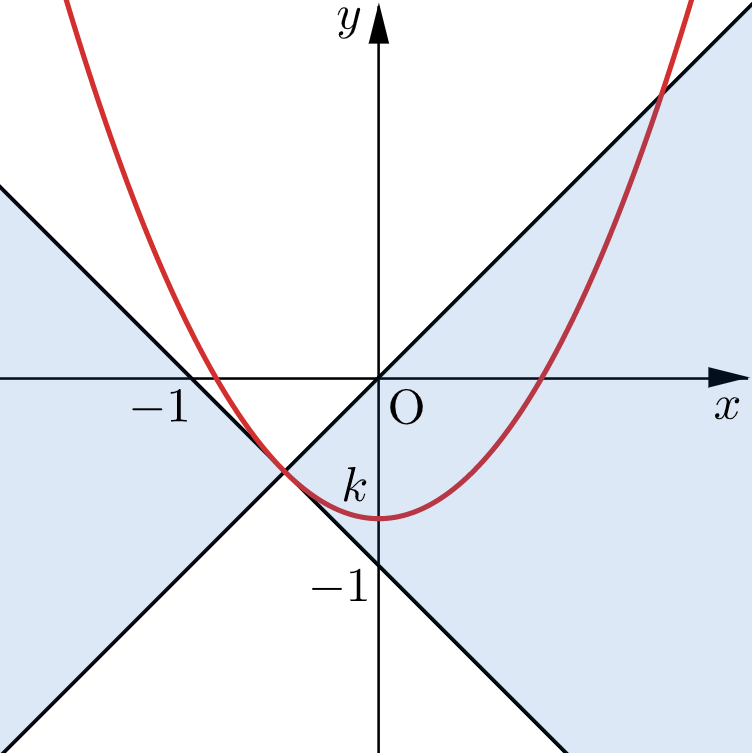
$-x-1-x^2=k$ すなわち $x^2+x+k+1=0$ の判別式が $0$ となるので
$$1-4(k+1)=0 \ \Longleftrightarrow \ k=-\dfrac{3}{4}$$

(ア),(イ)より、$k$ の最大値は $\dfrac{1}{4}$ である。

(ⅱ)　$\min(x-y^2, \ y-x^2)=x-y^2$ となるとき

(ⅰ)と同様に考えると、$x,\,y$ の対称性から、領域・放物線ともに直線 $y=x$ について(ⅰ)と対称な場合を考えればよいので、$k$ の最大値は(ⅰ)と同じく $\dfrac{1}{4}$ となる。

(ⅰ),(ⅱ)より、求める最大値は $\boldsymbol{\dfrac{1}{4}}$ である。

解説

$\min$ は最小値のことですが、丁寧に定義が書かれているので、これを利用して式変形を行いましょう。

領域を図示した後は、その領域と放物線が共有点をもつときを考えるという定番の流れで、「線形計画法」の問題をこなしていれば自然と発想できるのではないでしょうか。

解答のように、対称性に注目すれば記述量を半分に減らせます。

まとめ

今回は、一橋大学数学（2022年後期 第3問）の解説をしました。