京都大学 理系数学 2022年 第5問 解説

今回は、京都大学理系数学（2022年 第5問）の解説をしたいと思います。

問題

　曲線 $C:y={\cos }^{3}x(0\leqq x\leqq {\displaystyle \frac{\pi }{2}})$，$x$ 軸および $y$ 軸で囲まれる図形の面積を $S$ とする．$0<t<{\displaystyle \frac{\pi }{2}}$ とし，$C$ 上の点 $\mathrm{Q}(t,{\cos }^{3}t)$ と原点 $\mathrm{O}$，および $\mathrm{P}(t,0)$，$\mathrm{R}(0,{\cos }^{3}t)$ を頂点にもつ長方形 $\mathrm{OPQR}$ の面積を $f(t)$ とする．このとき，次の各問に答えよ．

⑴　$S$ を求めよ．

⑵　$f(t)$ は最大値をただ $1$ つの $t$ でとることを示せ．そのときの $t$ を $\alpha$ とすると，$f(\alpha )={\displaystyle \frac{{\cos }^4\alpha }{3\sin \alpha }}$ であることを示せ．

⑶　${\displaystyle \frac{f(\alpha )}{S}}<{\displaystyle \frac{9}{16}}$ を示せ．

（京都大学）

解答

⑴

$0\leqq x\leqq {\displaystyle \frac{\pi }{2}}$ において ${\cos }^{3}x\geqq 0$ であり、${\cos }^3{\displaystyle \frac{\pi }{2}}=0$ であるから、グラフの概形は次のようになる。

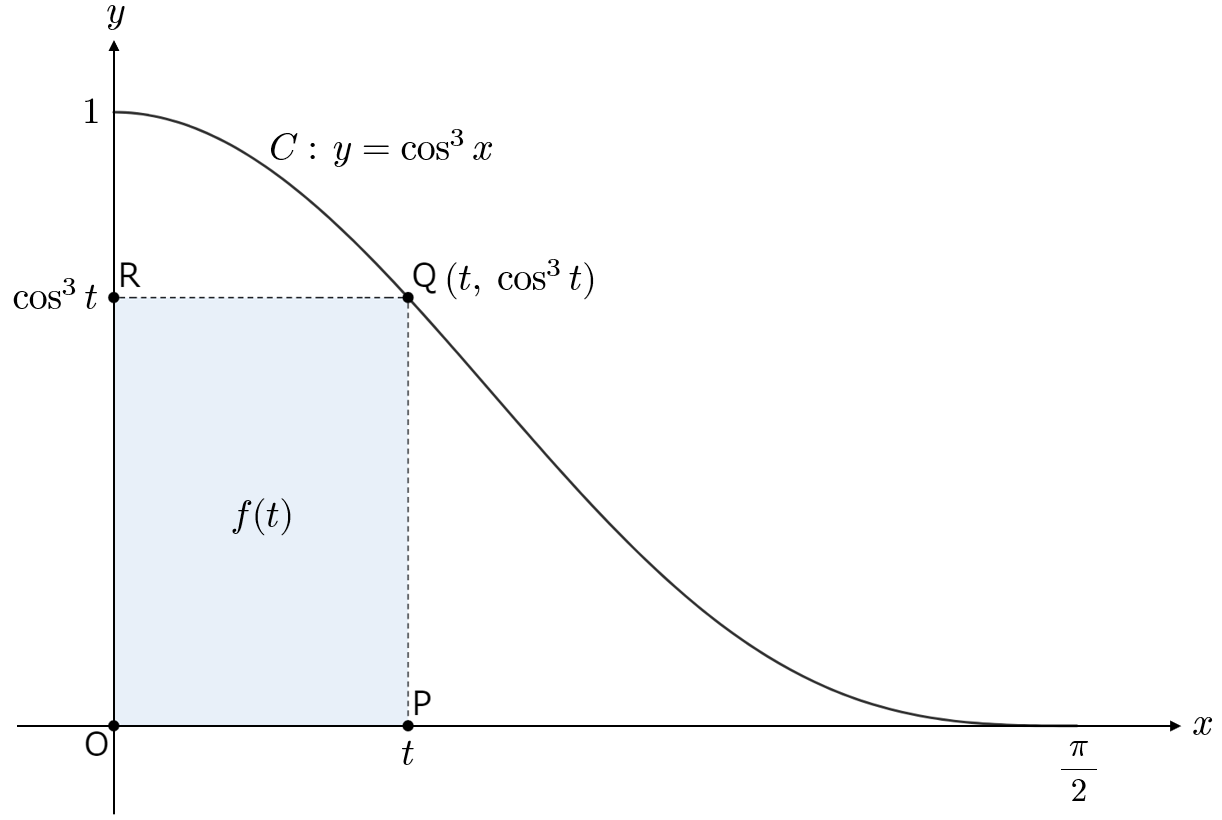
解法1

$$\begin{array}{rcl}S& =& {\displaystyle {\int }_0^{\frac{\pi }{2}}{\cos }^{3}xdx}\\ & =& {\displaystyle {\int }_0^{\frac{\pi }{2}}(1-{\sin }^{2}x)\cos xdx}\\ & =& {[\sin x–{\displaystyle \frac{1}{3}}{\sin }^{3}x]}_0^{\frac{\pi }{2}}\\ & =& {\displaystyle \frac{\mathbf{2}}{\mathbf{3}}}\end{array}$$

解法2

$\cos 3x=4{\cos }^{3}x–3\cos x$ より ${\cos }^{3}x={\displaystyle \frac{\cos 3x+3\cos x}{4}}$ なので
$$\begin{array}{rcl}S& =& {\displaystyle {\int }_0^{\frac{\pi }{2}}{\cos }^{3}xdx}\\ & =& {\displaystyle {\int }_0^{\frac{\pi }{2}}{\displaystyle \frac{\cos 3x+3\cos x}{4}}dx}\\ & =& {\displaystyle \frac{1}{4}}{[{\displaystyle \frac{1}{3}}\sin 3x+3\sin x]}_0^{\frac{\pi }{2}}\\ & =& {\displaystyle \frac{\mathbf{2}}{\mathbf{3}}}\end{array}$$

⑵

$f(t)=t{\cos }^{3}t$ より
$$\begin{array}{rcl}{f}^{\prime }(t)& =& {\cos }^{3}t+t\cdot 3{\cos }^{2}t(-\sin t)\\ & =& {\cos }^{3}t(1-3t\tan t)\end{array}$$

$g(t)=1-3t\tan t$ とおくと、$0<t<{\displaystyle \frac{\pi }{2}}$ において $f^{\prime }(t)$ の符号は $g(t)$ の符号と一致し、$g(t)$ は単調減少である。

また
$$g(0)=1>0,{\displaystyle \underset{t\to \frac{\pi }{2}–0}{lim}g(t)=-\mathrm{\infty }<0}$$より、$0<t<{\displaystyle \frac{\pi }{2}}$ において $g(t)=0$ を満たす $t$ がただ $1$ つ存在する。

この値を $t=t_0$ とすると、$f(t)$ の増減表は次のようになる。
$$\overline{)\begin{array}{cccccc}t& (0)& \cdots & t_0& \cdots & \left({\displaystyle \frac{\pi }{2}}\right)\\ f^{\prime }(t)& & +& 0& –& \\ f(t)& & <img\; draggable="false"\; role="img"\; class="emoji"\; alt="\nearrow "\; src="https://s.w.org/images/core/emoji/14.0.0/svg/2197.svg">& \text{最大}& <img\; draggable="false"\; role="img"\; class="emoji"\; alt="\searrow "\; src="https://s.w.org/images/core/emoji/14.0.0/svg/2198.svg">& \end{array}}$$

増減表より、$f(t)$ は最大値をただ $1$ つの $t(=t_0)$ でとる。$$\begin{array}{}\text{(証明終)}& \end{array}$$

題意より、$t_0=\alpha$ であるから
$$\begin{array}{rcl}g(\alpha )=1-3\alpha \tan \alpha & =& 0\\ ⟺\alpha & =& {\displaystyle \frac{\cos \alpha }{3\sin \alpha }}\end{array}$$であり、このとき
$$\begin{array}{rcl}f(\alpha )& =& \alpha {\cos }^3\alpha \\ & =& {\displaystyle \frac{\cos \alpha }{3\sin \alpha }}\cdot {\cos }^3\alpha ={\displaystyle \frac{{\cos }^4\alpha }{3\sin \alpha }}\end{array}$$$$\begin{array}{}\text{(証明終)}& \end{array}$$

⑶

$$\begin{array}{rcl}g\left({\displaystyle \frac{\pi }{6}}\right)& =& 1-3\cdot {\displaystyle \frac{\pi }{6}}\tan {\displaystyle \frac{\pi }{6}}\\ & =& 1-{\displaystyle \frac{\pi }{2\sqrt{3}}}={\displaystyle \frac{2\sqrt{3}-\pi }{2\sqrt{3}}}\\ & >& {\displaystyle \frac{2\times 1.7-3.2}{2\sqrt{3}}}>0\end{array}$$

$g(t)$ は単調減少なので、$\alpha >{\displaystyle \frac{\pi }{6}}$ である。

また ${\displaystyle \frac{{\cos }^{4}t}{\sin t}}(0<t<{\displaystyle \frac{\pi }{2}})$ について、${\cos }^{4}t$ は単調減少、$\sin t$ は単調増加であるから、${\displaystyle \frac{{\cos }^{4}t}{\sin t}}$ は単調減少である。

よって
$$\begin{array}{rcl}{\displaystyle \frac{f(\alpha )}{S}}& =& {\displaystyle \frac{{\cos }^4\alpha }{3\sin \alpha }}÷{\displaystyle \frac{2}{3}}={\displaystyle \frac{{\cos }^4\alpha }{2\sin \alpha }}\\ & <& {\displaystyle \frac{{\cos }^4{\displaystyle \frac{\pi }{6}}}{2\sin {\displaystyle \frac{\pi }{6}}}}={\displaystyle \frac{{\left({\displaystyle \frac{\sqrt{3}}{2}}\right)}^4}{2\times {\displaystyle \frac{1}{2}}}}\\ & =& {\displaystyle \frac{9}{16}}\end{array}$$$$\begin{array}{}\text{(証明終)}& \end{array}$$

解説

⑴は単に計算するだけです。
${\cos }^{3}x$ の積分は、練習問題などで1度は経験しているはずの必修問題です。

⑵も証明問題ですから、流れに乗って計算すれば、安心して結論を導けるでしょう。

⑶は答えを見れば簡単ですが、なかなか初見では発想できないかもしれません。
反対に、
$${\displaystyle \frac{{\cos }^4{\displaystyle \frac{\pi }{6}}}{2\sin {\displaystyle \frac{\pi }{6}}}}={\displaystyle \frac{{\left({\displaystyle \frac{\sqrt{3}}{2}}\right)}^4}{2\times {\displaystyle \frac{1}{2}}}}={\displaystyle \frac{9}{16}}$$に気づければ、この問題はもらったも同然でしょう。

また、$\alpha >{\displaystyle \frac{\pi }{6}}$ を示す上で、本解答では $\pi <3.2$ を用いました。$\pi \fallingdotseq 3.14$ は常識ですから、この式も当たり前に使えそうです。

使えそうですが、果たして「自明」と言って良いのでしょうか？
「正多角形に内接する円」など余計なことを考えなくて良いように、「 $\pi <3.2$ は証明なしに用いてよい」などの文言があればなお良かったかなと思います。

まとめ

今回は、京都大学理系数学（2022年 第5問）の解説をしました。