今回は、京都大学理系数学(2022年 第4問)の解説をしたいと思います。
問題
四面体 $\mathrm{OABC}$ が
$$\begin{array}{l}
\mathrm{OA}=4, \\
\mathrm{OB=AB=BC}=3, \\
\mathrm{OC=AC}=2 \sqrt{ 3 }
\end{array}$$を満たしているとする.$\mathrm{P}$ を辺 $\mathrm{BC}$ 上の点とし,$\triangle \mathrm{OAP}$ の重心を $\mathrm{G}$ とする.このとき,次の各問に答えよ.⑴ $\overrightarrow{ \mathrm{PG} } \perp \overrightarrow{ \mathrm{OA} }$ を示せ.
⑵ $\mathrm{P}$ が辺 $\mathrm{BC}$ 上を動くとき,$\mathrm{PG}$ の最小値を求めよ.
(京都大学)
解答
⑴
解法1(幾何)
辺 $\mathrm{OA}$ の中点を $\mathrm{M}$ とする。
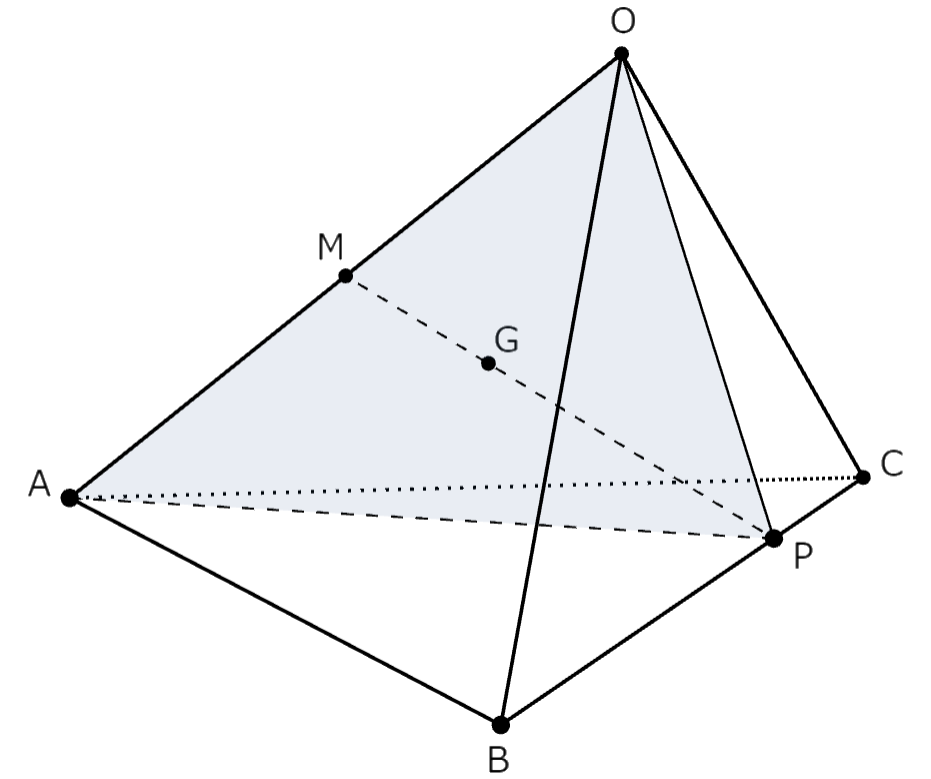
$\triangle \mathrm{OBC}$ と $\triangle \mathrm{ABC}$ について
$$\begin{eqnarray}
\left\{
\begin{array}{l}
\mathrm{OB=AB} \ (=3) \\
\mathrm{BC=BC} \\
\mathrm{OC=AC} \ \big(\!=2 \sqrt{ 3 }\big)
\end{array}
\right.
\end{eqnarray}$$より、$3$ 組の辺がそれぞれ等しいので $\triangle \mathrm{OBC} \equiv \triangle \mathrm{ABC}$ である。
すなわち、$\angle \mathrm{OBC} = \angle \mathrm{ABC}$ である。
さらに、$\mathrm{P}$ が辺 $\mathrm{BC}$ 上にあることを考慮すると、$\triangle \mathrm{OBP}$ と $\triangle \mathrm{ABP}$ について
$$\begin{eqnarray}
\left\{
\begin{array}{l}
\mathrm{OB=AB} \ (=3) \\
\mathrm{BP=BP} \\
\angle \mathrm{OBP} = \angle \mathrm{ABP}
\end{array}
\right.
\end{eqnarray}$$より、$2$ 組の辺とその間の角がそれぞれ等しいので $\triangle \mathrm{OBP} \equiv \triangle \mathrm{ABP}$ である。
よって、$\mathrm{OP} = \mathrm{AP}$ であるから、$\triangle \mathrm{OAP}$ は二等辺三角形である。
したがって、$\mathrm{PM} \perp \mathrm{OA}$ であり、$\triangle \mathrm{OAP}$ の重心である $\mathrm{G}$ は辺 $\mathrm{PM}$ 上の点であるから、$$\overrightarrow{ \mathrm{PG} } \perp \overrightarrow{ \mathrm{OA} }$$$$\tag{証明終}$$
解法2(ベクトル)
$\overrightarrow{ \mathrm{OA} } = \overrightarrow{ a }, \ \overrightarrow{ \mathrm{OB} } = \overrightarrow{ b }, \ \overrightarrow{ \mathrm{OC} } = \overrightarrow{ c }$ とおく。
$$\begin{eqnarray}
\big| \ \overrightarrow{ a } \ \big| &=& \mathrm{OA} = 4 \\
\big| \ \overrightarrow{ b } \ \big| &=& \mathrm{OB} = 3 \\
\big| \ \overrightarrow{ c } \ \big| &=& \mathrm{OC} = 2 \sqrt{ 3 } \\[0.5em]
\overrightarrow{ \mathstrut a } \cdot \overrightarrow{ \mathstrut b } &=& \dfrac{\mathrm{OA}^2+\mathrm{OB}^2-\mathrm{AB}^2}{2} \\
&=& \dfrac{4^2+3^2-3^2}{2} = 8 \\[0.5em]
\overrightarrow{ \mathstrut b } \cdot \overrightarrow{ \mathstrut c } &=& \dfrac{\mathrm{OB}^2+\mathrm{OC}^2-\mathrm{BC}^2}{2} \\
&=& \dfrac{3^2+\big(2 \sqrt{ 3 }\big)^2-3^2}{2} = 6 \\[0.5em]
\overrightarrow{ c } \cdot \overrightarrow{ a } &=& \dfrac{\mathrm{OC}^2+\mathrm{OA}^2-\mathrm{CA}^2}{2} \\
&=& \dfrac{\big(2 \sqrt{ 3 }\big)^2+4^2-\big(2 \sqrt{ 3 }\big)^2}{2} = 8
\end{eqnarray}$$
辺 $\mathrm{OA}$ の中点を $\mathrm{M}$ とすると、
$$\overrightarrow{ \mathrm{OM} } = \dfrac{1}{2} \ \overrightarrow{ a }$$
$t$ を $0 \leqq t \leqq 1$ を満たす実数とし、$\mathrm{BP} : \mathrm{PM} = t : (1-t)$ とすると
$$\overrightarrow{ \mathrm{OP} } = (1-t)\overrightarrow{ b } + t\overrightarrow{ c }$$
$\mathrm{G}$ は $\triangle \mathrm{OAP}$ の重心であり、辺 $\mathrm{PM}$ を $2:1$ に内分するので、
$$\begin{eqnarray}
\overrightarrow{ \mathrm{PG} } &=& \dfrac{2}{3} \overrightarrow{ \mathrm{PM} } \\
&=& \dfrac{2}{3} ( \overrightarrow{ \mathrm{OM} } \ – \ \overrightarrow{ \mathrm{OP} } ) \\
&=& \dfrac{2}{3} \left[ \dfrac{1}{2} \ \overrightarrow{ a } \ – \ \Big\{ (1-t)\overrightarrow{ b } + t \ \overrightarrow{ c } \ \Big\} \right] \\
&=& \dfrac{1}{3} \Big\{ \ \overrightarrow{ a } \ – \ 2(1-t)\overrightarrow{ b } \ – \ 2t \ \overrightarrow{ c } \ \Big\}
\end{eqnarray}$$
よって
$$\begin{eqnarray}
\overrightarrow{ \mathrm{PG} } \cdot \overrightarrow{ \mathrm{OA} } &=& \dfrac{1}{3} \Big\{ \ \overrightarrow{ a } \ – \ 2(1-t)\overrightarrow{ b } \ – \ 2t \ \overrightarrow{ c } \ \Big\} \cdot \overrightarrow{ a } \\
&=& \dfrac{1}{3} \Big\{ \big| \ \overrightarrow{ a } \ \big|^2 \ – \ 2(1-t)\overrightarrow{ \mathstrut a } \cdot \overrightarrow{ \mathstrut b } \ – \ 2t \ \overrightarrow{ c } \cdot \overrightarrow{ a } \ \Big\} \\
&=& \dfrac{1}{3} \big\{ 4^2 \ – \ 2(1-t) \cdot 8 \ – \ 2t \cdot 8 \big\} \\[0.3em]
&=& 0
\end{eqnarray}$$
したがって$$\overrightarrow{ \mathrm{PG} } \perp \overrightarrow{ \mathrm{OA} }$$$$\tag{証明終}$$
⑵
解法1
$\mathrm{PG} = \dfrac{2}{3} \mathrm{PM} \quad \cdots \text{①}$ であるから、$\mathrm{PG}$ が最小となるのは $\mathrm{PM}$ が最小となるときである。
また、$\triangle \mathrm{OMP}$ は $\angle \mathrm{OMP} = 90 ^{\circ}$ の直角三角形であり、
$$\begin{eqnarray}
\mathrm{PM} &=& \sqrt{ \mathrm{OP}^2 \ – \ \mathrm{OM}^2 } \\
&=& \sqrt{ \mathrm{OP}^2 \ – \ 2^2 } = \sqrt{ \mathrm{OP}^2 \ – \ 4 } \quad \cdots \text{②}
\end{eqnarray}$$なので、$\mathrm{PM}$ が最小となるのは $\mathrm{OP}$ が最小となるときである。
ここで $\triangle \mathrm{OBC}$ について、最大の辺は $\mathrm{OC} = 2 \sqrt{ 3 }$ であり、
$$\mathrm{OB}^2 + \mathrm{BC}^2 \ – \ \mathrm{OC}^2 = 3^2 +3^2 \ – \ \big(2 \sqrt{ 3 }\big)^2 = 6>0$$なので、$\triangle \mathrm{OBC}$ は鋭角三角形である。
よって、$\mathrm{OP}$ が最小となるのは、$\mathrm{OP} \perp \mathrm{BC}$ となるときである。
$\triangle \mathrm{OBC}$ の面積は
$$\dfrac{1}{2} \times 2 \sqrt{ 3 } \times \sqrt{ 3^2 \ – \ \left( \dfrac{2 \sqrt{ 3 }}{2} \right)^2 } = 3 \sqrt{ 2 }$$であるから、辺 $\mathrm{BC}$ を底辺としたときの $\triangle \mathrm{OBC}$ の高さを $h$ とすると、
$$\begin{eqnarray}
\dfrac{1}{2} \cdot \mathrm{BC} \cdot h &=& 3 \sqrt{ 2 } \\[0.5em]
h &=& \dfrac{2 \times 3 \sqrt{ 2 }}{\mathrm{BC}} = \dfrac{6 \sqrt{ 2 }}{3} = 2 \sqrt{ 2 }
\end{eqnarray}$$
これが $\mathrm{OP}$ の最小値であるから、①,②より、$\mathrm{PG}$ の最小値は
$$\dfrac{2}{3} \times \sqrt{ \big(2 \sqrt{ 2 }\big)^2 \ – \ 4 } = \mathbf{\dfrac{4}{3}}$$
解法2
$$\overrightarrow{ \mathrm{PG} } = \dfrac{1}{3} \Big\{ \ \overrightarrow{ a } \ – \ 2(1-t)\overrightarrow{ b } \ – \ 2t \ \overrightarrow{ c } \ \Big\}$$より、
$$\begin{eqnarray}
\big|\overrightarrow{ \mathrm{PG} }\big|^2 &=& \left| \dfrac{1}{3} \Big\{ \ \overrightarrow{ a } \ – \ 2(1-t)\overrightarrow{ b } \ – \ 2t \ \overrightarrow{ c } \ \Big\} \right|^2 \\
&=& \dfrac{1}{9} \Big\{ \big| \ \overrightarrow{ a } \ \big|^2+4(1-t)^2\big| \ \overrightarrow{ b } \ \big|^2+4t^2\big| \ \overrightarrow{ c } \ \big|^2-4(1-t)\overrightarrow{ \mathstrut a }\cdot\overrightarrow{ \mathstrut b }+8t(1-t)\overrightarrow{ \mathstrut b }\cdot\overrightarrow{ \mathstrut c }-4t \ \overrightarrow{ c }\cdot\overrightarrow{ a } \ \Big\} \\
&=& \dfrac{1}{9} \big\{ 4^2+4(1-t)^2\cdot 3^2+4t^2\cdot \big(2 \sqrt{ 3 }\big)^2-4(1-t) \cdot 8+8t(1-t) \cdot 6-4t \cdot 8 \big\} \\
&=& 4 \left( t-\dfrac{1}{3} \right)^2+\dfrac{16}{9}
\end{eqnarray}$$
$0 \leqq t \leqq 1$ より、$\big|\overrightarrow{ \mathrm{PG} }\big|^2$ の最小値は $\dfrac{16}{9} \ \left(t=\dfrac{1}{3}\right.$ のとき$\bigg)$ であるから、$\mathrm{PG}$ の最小値は
$$\sqrt{ \dfrac{16}{9} } = \mathbf{\dfrac{4}{3}}$$
$$\mathbf{\dfrac{4}{3}}$$
解説
⑴がベクトル表記で出題されているため、「ベクトルで解かなければ」という先入観が働きますが、計算が複雑でけっこう面倒くさいです。
本問は三角錐のすべての辺の長さが分かっており、すべての面が二等辺三角形となっているため、幾何による解法もそこまで難しくなく、計算も比較的シンプルです。
ですが、ベクトルで解いた場合も、$\overrightarrow{ \mathrm{PG} } \cdot \overrightarrow{ \mathrm{OA} }$ を計算すると( $s$ が消えて)$0$ になり、$\mathrm{P}$ の位置によらず $\overrightarrow{ \mathrm{PG} } \perp \overrightarrow{ \mathrm{OA} }$ が成り立つのを確かめられた瞬間は気持ちいいですね。
また⑵に関して、細かいところですが、「$\mathrm{OP}$ が最小となるのは、$\mathrm{OP} \perp \mathrm{BC}$ となるとき」であることを言うためには、「$\angle \mathrm{OBC}$ と $\angle \mathrm{OCB}$ がともに鋭角」であることを示しておく必要があります。
例えば $\angle \mathrm{OBC}$ が鈍角である場合、$\mathrm{OP}$ が最小となるのは、$\mathrm{OP} \perp \mathrm{BC}$ となるときではなく、$\mathrm{P}$ が $\mathrm{B}$ と一致するときです。
($\mathrm{P}$ は辺 $\mathrm{BC}$ 上の点なので、$\angle \mathrm{OBC}$ が鈍角のとき、$\mathrm{OP} \perp \mathrm{BC}$ は成り立ちません。)
本解答では、さらに強い条件として「$\triangle \mathrm{OBC}$ が鋭角三角形」であることを示しているため、十分です。
同じ問題でも(ベクトルや幾何など)いろいろな解き方があるという点では、難関大ならではの問題だったと言えます。
まとめ
今回は、京都大学理系数学(2022年 第4問)の解説をしました。
ほかの問題にもチャレンジしよう!
京都大学 理系数学 2022年 第1問 解説
京都大学 理系数学 2022年 第2問 解説
京都大学 理系数学 2022年 第3問 解説
京都大学 理系数学 2022年 第4問 解説
京都大学 理系数学 2022年 第5問 解説
京都大学 理系数学 2022年 第6問 解説













