今回は、東京大学理系数学(2018年 第5問)の解説をしたいと思います。
問題
複素数平面上の原点を中心とする半径 $1$ の円を $C$ とする。点 $\mathrm{P}(z)$ は $C$ 上にあり,点 $\mathrm{A}(1)$ とは異なるとする。点 $\mathrm{P}$ における円 $C$ の接線に関して,点 $\mathrm{A}$ と対称な点を $\mathrm{Q}(u)$ とする。$w=\dfrac{1}{1-u}$ とおき,$w$ と共役な複素数を $\overline{w}$ で表す。
⑴ $u$ と $\dfrac{\overline{w}}{w}$ を $z$ についての整式として表し,絶対値の商 $\dfrac{|\,w+\overline{w}-1\,|}{|\,w\,|}$ を求めよ。
⑵ $C$ のうち実部が $\dfrac{1}{2}$ 以下の複素数で表される部分を $C’$ とする。点 $\mathrm{P}(z)$ が $C’$ 上を動くときの点 $\mathrm{R}(w)$ の軌跡を求めよ。
(東京大学)
解答
⑴
$z$ の偏角を $\theta$ とおく。
(ⅰ) $0\lt\theta\lt\pi$ のとき
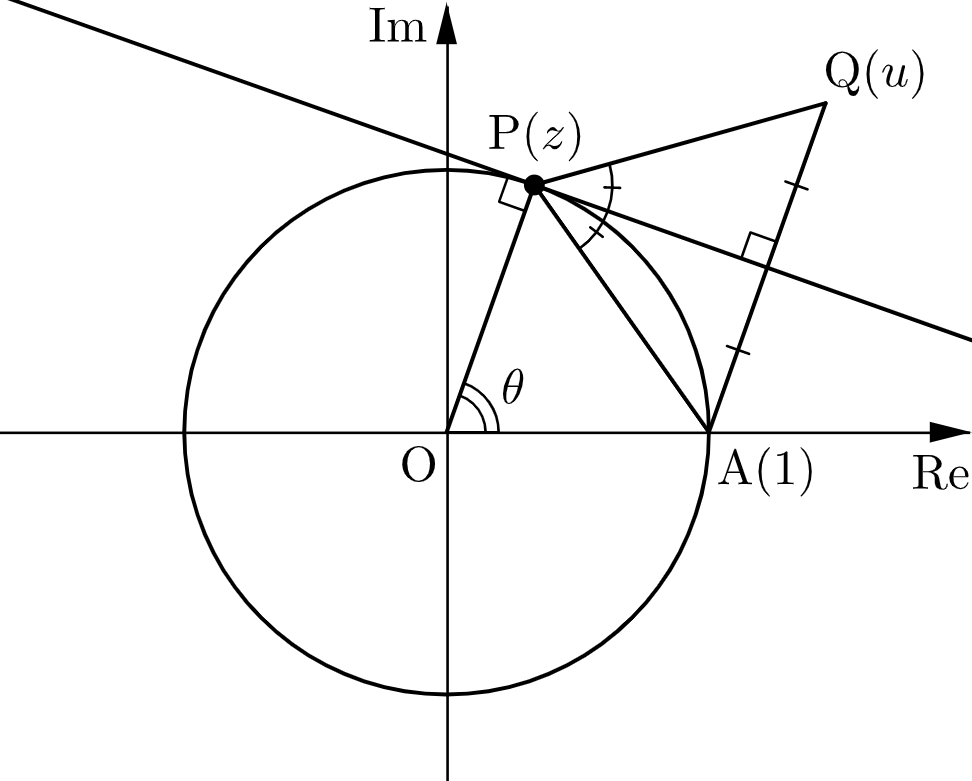
円周角と中心角の関係および接弦定理により
$$\angle\mathrm{APQ}=2\cdot\dfrac{\theta}{2}=\theta.$$
$\mathrm{PA}=\mathrm{PQ}$ より、$\mathrm{Q}$ は点 $\mathrm{P}$ を中心として $\theta$ だけ回転した点である。
$\cos\theta+i\sin\theta=z$ より
$$\begin{align}
u-z &= (\cos\theta+i\sin\theta)(1-z) \\[0.3em]
\therefore \ u &= z(1-z)+z \\
&= 2z-z^2. \quad\cdots\text{①}
\end{align}$$
(ⅱ) $\theta=\pi$ のとき
$z=-1$,$u=-3$ より、①が成り立つ。
(ⅲ) $-\pi\lt\theta\lt0$ のとき
点 $\mathrm{P},\,\mathrm{Q}$ を実軸に関して対称移動すると、(ⅰ)と同じ状況となるので
$$\overline{u}=2\overline{z}-\overline{z}^{\,2}.$$両辺の共役な複素数を考えると、①が成り立つ。
(ⅰ)~(ⅲ)より、$u=\boldsymbol{2z-z^2}.$
ここで、$\mathrm{P}$ は $C$ 上の点なので $|\,z\,|=1$ であり、両辺を $2$ 乗すると $|\,z\,|^2=z\overline{z}=1.$
$z\ne0$ より $\overline{z}=\dfrac{1}{z}.$
$$w=\dfrac{1}{1-2z+z^2}=\dfrac{1}{(z-1)^2} \quad\cdots\text{②}$$より
$$\begin{align}
\dfrac{\overline{w}}{w} &= \dfrac{(z-1)^2}{(\overline{z}-1)^2} \\
&= \dfrac{(z-1)^2}{\left(\dfrac{1}{z}-1\right)^2} \\
&= \left\{\dfrac{z(z-1)}{1-z}\right\}^2 \\[0.2em]
&= \boldsymbol{z^2}.
\end{align}$$
さらに
$$\begin{align}
\dfrac{|\,w+\overline{w}-1\,|}{|\,w\,|} &= \left|\,1+\dfrac{\overline{w}}{w}-\dfrac{1}{w}\,\right| \\
&= |\,1+z^2-(z-1)^2\,| \\[0.2em]
&= 2|\,z\,| \\[0.2em]
&= \mathbf{2}.
\end{align}$$
別解
※ $u$ を求める別解です。
$xy$ 座標平面上で考える。$\mathrm{P}(p,\,q)$,$\mathrm{Q}(s,\,t)$ とする。
点 $\mathrm{P}$ における円 $C$ の接線($\,\ell$ とする。)の方程式は
$$px+qy=1$$であり、線分 $\mathrm{AQ}$ の中点はこの接線上にあるので
$$\begin{align}
p\cdot\dfrac{s+1}{2}+q\cdot\dfrac{t+0}{2} &= 1 \\[0.2em]
\therefore \ ps+p+qt &= 2. \quad\cdots\text{ⓐ}
\end{align}$$
また、$\ell$ の方向ベクトルの $1$ つは $(q,\,-p)$ であり、$\ell\perp\overrightarrow{\mathrm{AQ}}$ なので
$$\begin{align}
(q,\,-p)\cdot(s-1,\,t) &= 0 \\[0.2em]
\therefore \ qs-q-pt &= 0. \quad\cdots\text{ⓑ}
\end{align}$$
$p^2+q^2=1$ に注意すると、ⓐ,ⓑより
$$s=1+2p-2p^2,\quad t=2q(1-p).$$
ここで
$$p=\dfrac{z+\overline{z}}{2},\quad q=\dfrac{z-\overline{z}}{2i}$$であるから、複素数平面上において
$$\begin{align}
u &= s+ti \\[0.2em]
&= (1+2p-2p^2)+2q(1-p)i \\
&= 1+z+\overline{z}-\dfrac{z^2+2z\overline{z}+\overline{z}^{\,2}}{2}+(z-\overline{z})\left(1-\dfrac{z+\overline{z}}{2}\right) \\
&= 1+z+\overline{z}-\dfrac{z^2}{2}-1-\dfrac{\overline{z}^{\,2}}{2}+z-\overline{z}-\dfrac{z^2}{2}+\dfrac{\overline{z}^{\,2}}{2} \\[0.2em]
&\hphantom{=}\text{(}\because z\overline{z}=|\,z\,|^2=1\,\text{)} \\[0.3em]
&= \boldsymbol{2z-z^2}.
\end{align}$$
$$\begin{array}{l}
u=\boldsymbol{2z-z^2},\quad\dfrac{\overline{w}}{w}=\boldsymbol{z^2}, \\
\dfrac{|\,w+\overline{w}-1\,|}{|\,w\,|}=\mathbf{2}
\end{array}$$
⑵
$w=x+yi$($\,x,\,y$ は実数)とおくと、⑴の結果より
$$\begin{align}
|\,w+\overline{w}-1\,| &= 2|\,w\,| \\[0.2em]
\therefore \ |\,2x-1\,| &= 2\sqrt{x^2+y^2}
\end{align}$$$(\text{両辺})\gt0$ より、両辺を $2$ 乗すると
$$\begin{align}
(2x-1)^2 &= 4(x^2+y^2) \\
\therefore \ x &= \dfrac{1}{4}-y^2. \quad\cdots\text{③}
\end{align}$$したがって、点 $\mathrm{R}(w)$ の軌跡は曲線③の一部である。
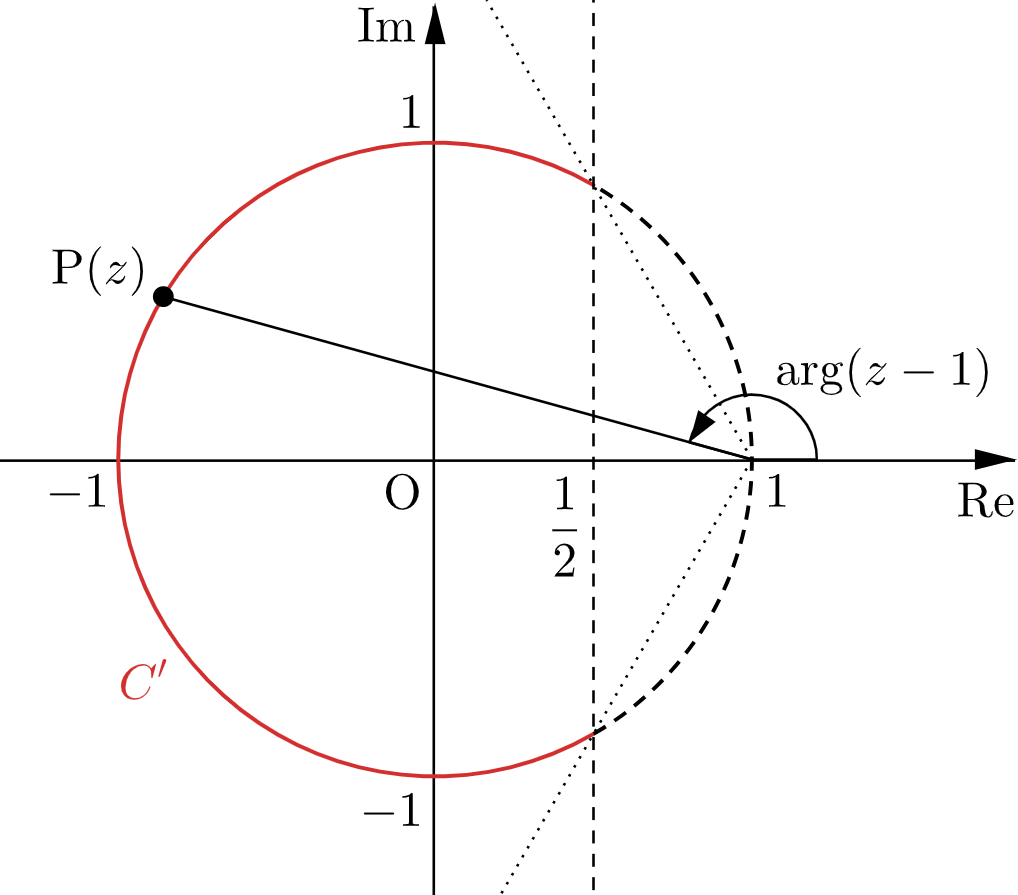
点 $\mathrm{P}$ が $C’$ 上を動くとき、上図より
$$\dfrac{2}{3}\pi\leqq\arg(z-1)\leqq\dfrac{4}{3}\pi.$$
ここで、②より
$$\begin{align}
\arg w &= \arg\left\{\dfrac{1}{(z-1)^2}\right\} \\
&= -\arg(z-1)^2 \\[0.2em]
&= -2\arg(z-1)
\end{align}$$であり
$$-\dfrac{8}{3}\pi\leqq-2\arg(z-1)\leqq-\dfrac{4}{3}\pi$$なので
$$-\dfrac{2}{3}\pi\leqq\arg w\leqq\dfrac{2}{3}\pi.$$
$x\lt0$ における曲線③と直線 $y=\left\{\tan\left(\pm\dfrac{2}{3}\pi\right)\right\}x$(すなわち直線 $y=\pm\sqrt{3}x\,$)の交点の座標は $\bigg(-\dfrac{1}{2},\,\pm\dfrac{\sqrt{3}}{2}\bigg)$ となる。
以上より、求める軌跡は、$w=x+yi$ とおいたときの放物線 $\boldsymbol{x=\dfrac{1}{4}-y^2}$ の $\boldsymbol{x\geqq-\dfrac{1}{2}}$ の部分である。
なお、これを複素数平面上に図示すると、下図の実線部のようになる。
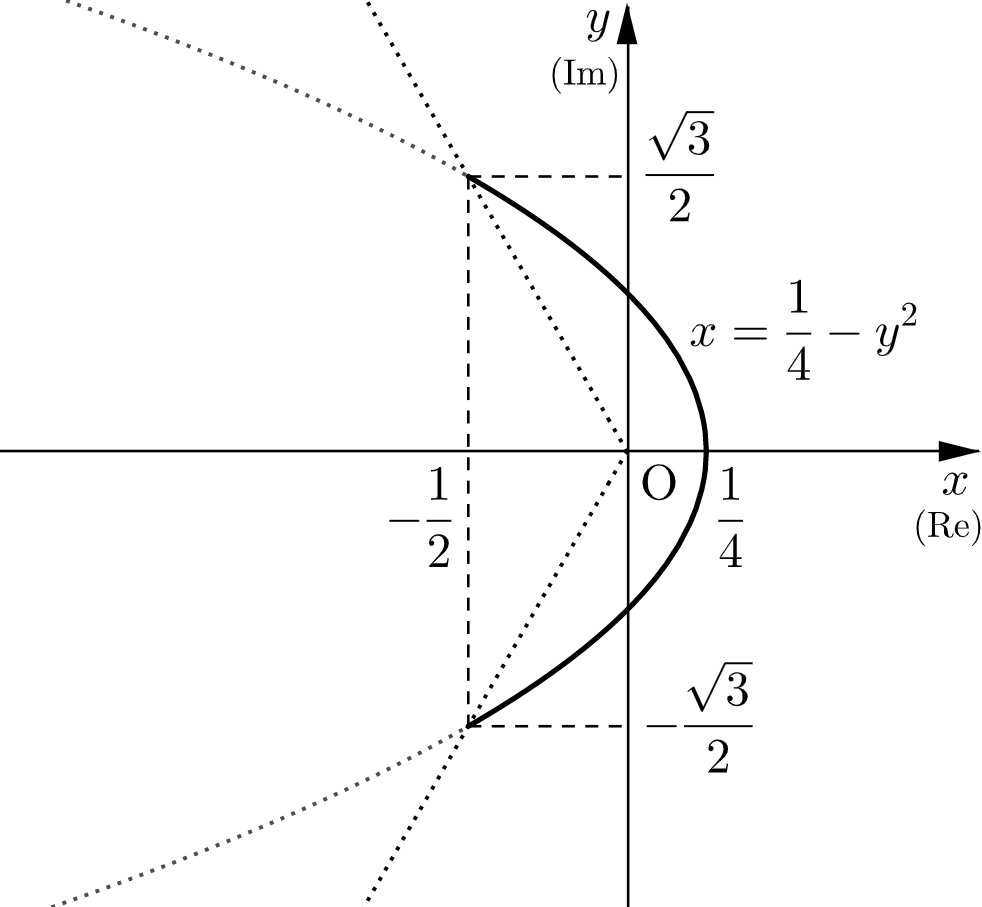
放物線 $\boldsymbol{x=\dfrac{1}{4}-y^2}$ の $\boldsymbol{x\geqq-\dfrac{1}{2}}$ の部分
複素数平面上では下図の実線部

解説
⑴は、$u$ を求めるのがいきなりの山場です。点の線対称移動を複素数で表現できるか問われています。
接線も絡んでおり、垂直・平行・三角形の合同をうまく処理して答えを求めましょう。
$u$ が求まったら、残りは基本的な複素数の計算です。
⑵は、⑴で求めた $\dfrac{|\,w+\overline{w}-1\,|}{|\,w\,|}=2$ からスタートします。
$\left|\,\dfrac{w+\overline{w}}{2}-\dfrac{1}{2}\,\right|=|\,w\,|$ すなわち $\left|\,\mathrm{Re}(w)-\dfrac{1}{2}\,\right|=|\,w\,|$ と変形して、$w$ は「直線 $x=\dfrac{1}{2}$ からの距離と原点からの距離が等しい点」なので「放物線 $x=\dfrac{1}{4}-y^2\,$」の上を動く、とも求められますが、この変形はトリッキーで見えにくいので、最初から $x+yi$ とおくのが無難だと思います。
実際に放物線のどの部分を動くかを求めるのは、少し難しいです。
この問題のように、軌跡の限界点を偏角に着目して別の式から求めるという手段は、覚えておいても良いと思います。
まとめ
今回は、東京大学理系数学(2018年 第5問)の解説をしました。
ほかの問題にもチャレンジしよう!
東京大学 理系数学 2018年 第1問 解説
東京大学 理系数学 2018年 第2問 解説
東京大学 理系数学 2018年 第3問 解説
東京大学 理系数学 2018年 第4問 解説
東京大学 理系数学 2018年 第5問 解説
東京大学 理系数学 2018年 第6問 解説













