東京大学 理系数学 2018年 第3問 解説

今回は、東京大学理系数学（2018年 第3問）の解説をしたいと思います。

問題

　放物線 $y=x^2$ のうち $-1\leqq x\leqq1$ をみたす部分を $C$ とする。座標平面上の原点 $\mathrm{O}$ と点 $\mathrm{A}(1,\,0)$ を考える。$k\gt0$ を実数とする。点 $\mathrm{P}$ が $C$ 上を動き，点 $\mathrm{Q}$ が線分 $\mathrm{OA}$ 上を動くとき，
$$\overrightarrow{\mathrm{OR}}=\dfrac{1}{k}\,\overrightarrow{\mathrm{OP}}+k\,\overrightarrow{\mathrm{OQ}}$$をみたす点 $\mathrm{R}$ が動く領域の面積を $S(k)$ とする。

　$S(k)$ および $\displaystyle\lim_{k\to+0}S(k)$，$\displaystyle\lim_{k\to\infty}S(k)$ を求めよ。

（東京大学）

解答

$-1\leqq p\leqq1$，$0\leqq q\leqq1$ を満たす実数 $p, \ $$q$ を用いて $\mathrm{P}(p,\,p^2)$，$\mathrm{Q}(q,\,0)$ とおく。

また、$\dfrac{1}{k}\,\overrightarrow{\mathrm{OP}}=\overrightarrow{\mathrm{OP}’}$，$k\,\overrightarrow{\mathrm{OQ}}=\overrightarrow{\mathrm{OQ}’}$ とおくと、$\mathrm{P}’\left(\dfrac{p}{k},\,\dfrac{p^2}{k}\right)$，$\mathrm{Q}'(kq,\,0)$ となる。

よって、点 $\mathrm{P}’$ は「放物線 $y=kx^2$ のうち $-\dfrac{1}{k}\leqq x\leqq\dfrac{1}{k}$ を満たす部分」$\cdots\text{①}$ を動き、点 $\mathrm{Q}’$ は $x$ 軸の $0\leqq x\leqq k$ を満たす部分を動く。

$$\overrightarrow{\mathrm{OR}}=\overrightarrow{\mathrm{OP}’}+\overrightarrow{\mathrm{OQ}’}$$であるから、点 $\mathrm{R}$ は①を $x$ 軸方向に $k$ だけ平行移動するときに①が通過する範囲を動く。

点 $\left(-\dfrac{1}{k},\,\dfrac{1}{k}\right)$ を $x$ 軸方向に $k$ だけ平行移動した点と 点 $\left(\dfrac{1}{k},\,\dfrac{1}{k}\right)$ の位置関係によって場合分けをする。

(ⅰ)　$-\dfrac{1}{k}+k\lt\dfrac{1}{k}$ すなわち $0\lt k\lt\sqrt{2}$ のとき

点 $\mathrm{R}$ が動く領域は下図の網掛け部分（境界を含む。）のようになる。

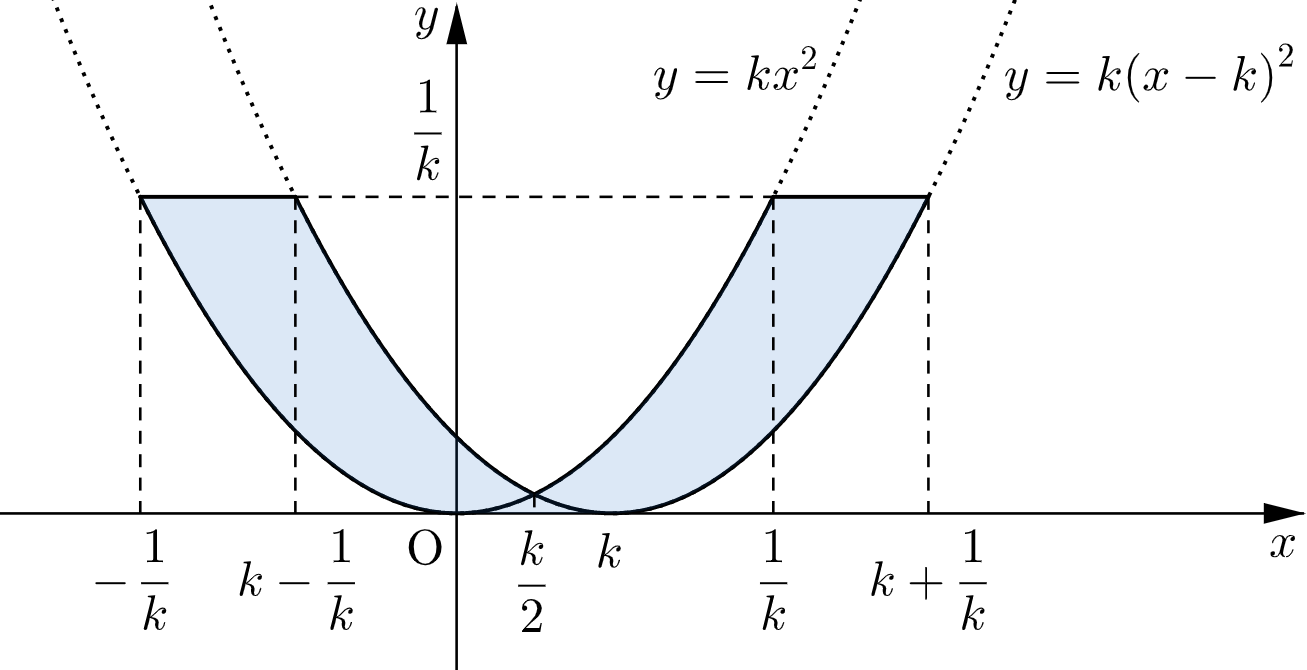
この領域は直線 $x=\dfrac{k}{2}$ に関して対称なので
$$\begin{align}
S(k) &= 2\cdot\bigg[\displaystyle\int_{-\frac{1}{k}}^{k-\frac{1}{k}}\left(\dfrac{1}{k}-kx^2\right)dx \\
&\hphantom{=} \ +\displaystyle\int_{k-\frac{1}{k}}^{0}\{k(x-k)^2-kx^2\}dx \\
&\hphantom{=} \ +\displaystyle\int_{0}^{\frac{k}{2}}k(x-k)^2dx\bigg] \\[0.3em]
\dfrac{S(k)}{2} &= \left[\dfrac{1}{k}x-\dfrac{k}{3}x^3\right]_{-\frac{1}{k}}^{k-\frac{1}{k}} \\
&\hphantom{=} \ +\left[\dfrac{k}{3}(x-k)^3-\dfrac{k}{3}x^3\right]_{k-\frac{1}{k}}^{0} \\
&\hphantom{=} \ +\left[\dfrac{k}{3}(x-k)^3\right]_{0}^{\frac{k}{2}} \\[0.3em]
&= 1-\dfrac{1}{k^2}-\dfrac{k}{3}\left(k-\dfrac{1}{k}\right)^3+\dfrac{1}{k^2}-\dfrac{1}{3k^2} \\
&\hphantom{=} \ -\dfrac{k^4}{3}+\dfrac{1}{3k^2}+\dfrac{k}{3}\left(k-\dfrac{1}{k}\right)^3 \\
&\hphantom{=} \ -\dfrac{k^4}{24}+\dfrac{k^4}{3} \\[0.3em]
&= 1-\dfrac{k^4}{24} \\[0.3em]
S(k) &= 2-\dfrac{k^4}{12}.
\end{align}$$

(ⅱ)　$-\dfrac{1}{k}+k\geqq\dfrac{1}{k}$ すなわち $k\geqq\sqrt{2}$ のとき

点 $\mathrm{R}$ が動く領域は下図の網掛け部分（境界を含む。）のようになる。

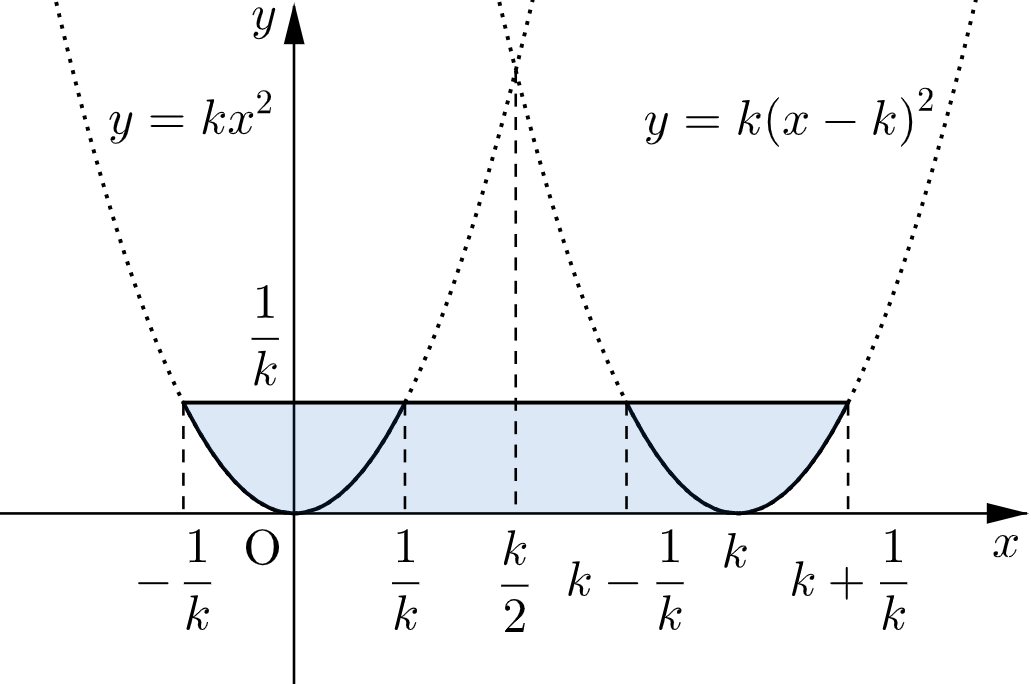
この領域は直線 $x=\dfrac{k}{2}$ に関して対称なので
$$\begin{align}
S(k) &= 2\cdot\bigg[\left\{\dfrac{k}{2}-\left(-\dfrac{1}{k}\right)\right\}\cdot\dfrac{1}{k}-\displaystyle\int_{-\frac{1}{k}}^{0}kx^2dx\bigg] \\
&= 2\cdot\bigg\{\left(\dfrac{k}{2}+\dfrac{1}{k}\right)\cdot\dfrac{1}{k}-\left[\dfrac{k}{3}x^3\right]_{-\frac{1}{k}}^{0}\bigg\} \\
&= 2\cdot\left(\dfrac{1}{2}+\dfrac{1}{k^2}-\dfrac{1}{3k^2}\right) \\
&= 1+\dfrac{4}{3k^2}.
\end{align}$$

(ⅰ),(ⅱ)より
$$S(k)=\left\{\begin{array}{ll}
\boldsymbol{2-\dfrac{k^4}{12}} & \mathbf{\text{（}}\,\boldsymbol{0\lt k\lt\sqrt{2}} \ \mathbf{\text{のとき）}} \\
\boldsymbol{1+\dfrac{4}{3k^2}} & \mathbf{\text{（}}\,\boldsymbol{k\geqq\sqrt{2}} \ \mathbf{\text{のとき）}}
\end{array}\right.$$

また
$$\begin{align}
\displaystyle\lim_{k\to+0}S(k) &= \displaystyle\lim_{k\to+0}\left(2-\dfrac{k^4}{12}\right)=\mathbf{2}, \\[0.3em]
\displaystyle\lim_{k\to\infty}S(k) &= \displaystyle\lim_{k\to\infty}\left(1+\dfrac{4}{3k^2}\right)=\mathbf{1}.
\end{align}$$

解説

図を描いて考えてみると、点 $\mathrm{R}$ が動く範囲は、放物線の一部を $x$ 軸方向に平行移動させたときの通過領域だと分かります。

また、$k$ の値が小さいときには領域が二股になり、$k$ の値が大きくなると横長の領域になることに気づくことがポイントです。

面積の求め方はいろいろありますが、効率的に求めると計算ミスも少なくなります。

例えば、$x$ 軸方向に $k$ だけ平行移動という性質を活かして、$y$ 軸に関して積分する方法もあります。ぜひ試してみましょう。

極限の計算は、$k\to+0$ と $k\to\infty$ で代入する $S(k)$ が異なることに注意しましょう。

まとめ

今回は、東京大学理系数学（2018年 第3問）の解説をしました。