京都大学 理系数学 2020年 第5問 解説

今回は、京都大学理系数学（2020年 第5問）の解説をしたいと思います。

問題

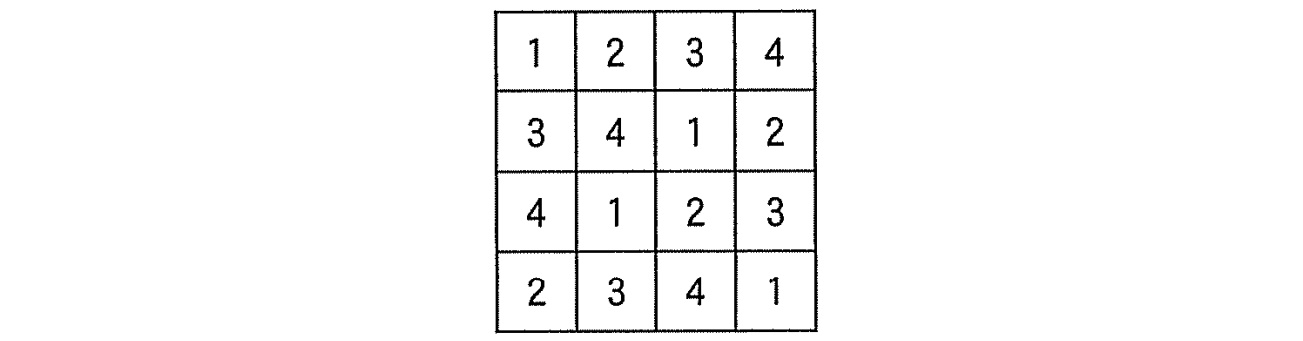
　縦 $4$ 個，横 $4$ 個のマス目のそれぞれに $1,\,$$2,\,$$3,\,$$4$ の数字を入れていく．このマス目の横の並びを行といい，縦の並びを列という．どの行にも，どの列にも同じ数字が $1$ 回しか現れない入れ方は何通りあるか求めよ．下図はこのような入れ方の $1$ 例である．

（京都大学）

解答

対称性より、一番上の行と一番左の列を
$$\begin{array}{|c|c|c|c|}\hline
1&2&3&4 \\ \hline
2&&& \\ \hline
3&&& \\ \hline
4&&& \\ \hline
\end{array}$$とし、この入れ方を $4!\times3!$ 倍したものが、求める入れ方の総数である。

上から $2$ 行目、左から $2$ 列目のマス目に入る数字を $\mathrm{A}$ とし、$\mathrm{A}$ の値によって場合分けをする。

(ⅰ)　$\mathrm{A}=1$ のとき

条件より、数字が確定するマス目を埋めると下図のようになる。
$$\begin{array}{|c|c|c|c|}\hline
1&2&3&4 \\ \hline
2&\color{red}{1}&4&3 \\ \hline
3&4&& \\ \hline
4&3&& \\ \hline
\end{array}$$

右下の $2\times2$ マスは $\begin{array}{|c|c|}\hline
1&2 \\ \hline
2&1 \\ \hline
\end{array}$ または $\begin{array}{|c|c|}\hline
2&1 \\ \hline
1&2 \\ \hline
\end{array}$ の $2$ 通りである。

(ⅱ)　$\mathrm{A}=3$ のとき

条件を満たすのは
$$\begin{array}{|c|c|c|c|}\hline
1&2&3&4 \\ \hline
2&\color{red}{3}&4&1 \\ \hline
3&4&1&2 \\ \hline
4&1&2&3 \\ \hline
\end{array}$$の $1$ 通りである。

(ⅲ)　$\mathrm{A}=4$ のとき

条件を満たすのは
$$\begin{array}{|c|c|c|c|}\hline
1&2&3&4 \\ \hline
2&\color{red}{4}&1&3 \\ \hline
3&1&4&2 \\ \hline
4&3&2&1 \\ \hline
\end{array}$$の $1$ 通りである。

(ⅰ),(ⅱ),(ⅲ)より、求める入れ方の総数は
$$4!\times3!\times(2+1+1)=\mathbf{576\text{（通り）}}$$

解説

設定はシンプルですが、求め方によっては場合分け・記述量が多くなるため注意です。

まずは一番上の行を $\begin{array}{|c|c|c|c|}\hline
1&2&3&4 \\ \hline\end{array}$ とする人が多いでしょうか。
これを $4!$ 倍したものが求める総数であることは、対称性より明らかです。

ここから、「一番左の列」と「上から $2$ 行目」のどちらを考えるかで、場合分けの量がだいぶ変わります。

解答のように「一番左の列」を考えた場合、「行の入れ替え」と「列の入れ替え」が互いに干渉しないので、$3!$ 倍とまとめられて簡単です。

いずれにせよ、答えだけは確実に合わせたい $1$ 問です。

まとめ

今回は、京都大学理系数学（2020年 第5問）の解説をしました。