京都大学 理系数学 2019年 第3問 解説

今回は、京都大学理系数学（2019年 第3問）の解説をしたいと思います。

問題

　鋭角三角形 $\mathrm{ABC}$ を考え，その面積を $S$ とする。$0\lt t\lt1$ をみたす実数 $t$ に対し，線分 $\mathrm{AC}$ を $t:1-t$ に内分する点を $\mathrm{Q}$，線分 $\mathrm{BQ}$ を $t:1-t$ に内分する点を $\mathrm{P}$ とする。実数 $t$ がこの範囲を動くときに点 $\mathrm{P}$ の描く曲線と，線分 $\mathrm{BC}$ によって囲まれる部分の面積を，$S$ を用いて表せ。

（京都大学）

解答

座標平面上において $\mathrm{A}(a,b)$，$\mathrm{B}(0,0)$，$\mathrm{C}(c,0)$ としても一般性を失わない。ただし、$\triangle\mathrm{ABC}$ が鋭角三角形であることから $0\lt a\lt c$，$b\gt0$ とする。

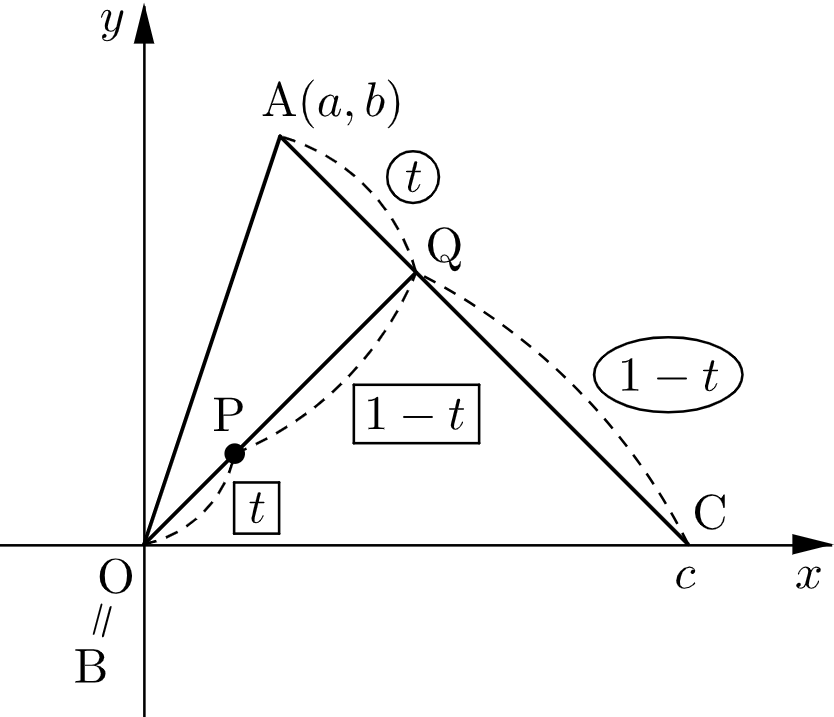
このとき
$$\begin{align}
\overrightarrow{\mathrm{BP}} &= t\overrightarrow{\mathrm{BQ}} \\
&= t\{(1-t)\overrightarrow{\mathrm{BA}}+t\,\overrightarrow{\mathrm{BC}}\} \\[0.2em]
&= t(1-t)\begin{pmatrix}a \\ b\end{pmatrix}+t^2\begin{pmatrix}c \\ 0\end{pmatrix} \\[0.2em]
&= \begin{pmatrix}at+(c-a)t^2 \\ b(t-t^2)\end{pmatrix}
\end{align}$$となるので、$\mathrm{P}(x,y)$ とすると
$$\left\{\begin{align}
x &= at+(c-a)t^2 \\[0.2em]
y &= bt(1-t)
\end{align}\right.$$となる。

$0\lt a\lt c$，$b\gt0$，$0\lt t\lt1$ において
$$\begin{array}{l}
\dfrac{dx}{dt}=a+2(c-a)t\gt0,\quad y\gt0, \\
\displaystyle\lim_{t\to+0}(x,y)=(0,0),\quad\displaystyle\lim_{t\to1-0}(x,y)=(c,0)
\end{array}$$となる。

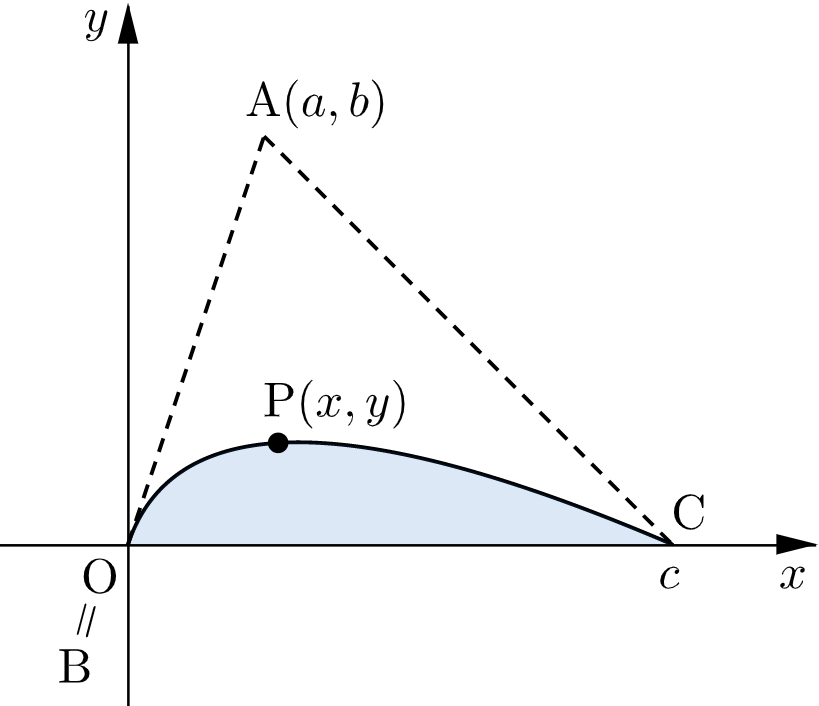
よって、点 $\mathrm{P}$ の描く曲線と線分 $\mathrm{BC}$ によって囲まれる部分の面積を $T$ とすると
$$\begin{align}
T &= \displaystyle\int_{0}^{c}y\,dx \\
&= \displaystyle\int_{0}^{1}y\dfrac{dx}{dt}dt \\
&= \displaystyle\int_{0}^{1}bt(1-t)\{a+2(c-a)t\}dt \\
&= b\displaystyle\int_{0}^{1}\{at+(2c-3a)t^2-2(c-a)t^3\}dt \\
&= b\left[\dfrac{a}{2}t^2+\dfrac{2c-3a}{3}t^3-\dfrac{c-a}{2}t^4\right]_{0}^{1} \\
&= b\left(\dfrac{a}{2}+\dfrac{2}{3}c-a-\dfrac{c}{2}+\dfrac{a}{2}\right) \\
&= \dfrac{bc}{6}
\end{align}$$となる。

$S=\dfrac{bc}{2}$ なので
$$T=\boldsymbol{\dfrac{S}{3}}$$

解説

「よく分からない軌跡で囲まれた面積」なので、座標を設定して積分という流れを発想するのが自然だと思います。

点 $\mathrm{P}$ の座標を $t$ を使って表せたら、あとは媒介変数表示された曲線に関する基本的な問題となります。

積分をして $a$ が消えるのかドキドキしますが、無事消えてくれるので $T$ を $S$ のみで表すことができます。

まとめ

今回は、京都大学理系数学（2019年 第3問）の解説をしました。