一橋大学 数学 2020年 第3問 解説

今回は、一橋大学数学（2020年 第3問）の解説をしたいと思います。

問題

　半径 $1$ の円周上に $3$ 点 $\mathrm{A},\,$$\mathrm{B},\,$$\mathrm{C}$ がある。内積 $\overrightarrow{\mathrm{AB}}\cdot\overrightarrow{\mathrm{AC}}$ の最大値と最小値を求めよ。

（一橋大学）

解答

座標平面上で原点 $\mathrm{O}$ を中心とする半径 $1$ の円を考える。

(ⅰ)　最大値について

$$\overrightarrow{\mathrm{AB}}\cdot\overrightarrow{\mathrm{AC}}=|\,\overrightarrow{\mathrm{AB}}\,||\,\overrightarrow{\mathrm{AC}}\,|\cos\angle\mathrm{BAC}$$であり、
$$|\,\overrightarrow{\mathrm{AB}}\,|\leqq2, \ |\,\overrightarrow{\mathrm{AC}}\,|\leqq2, \ \cos\angle\mathrm{BAC}\leqq1$$より
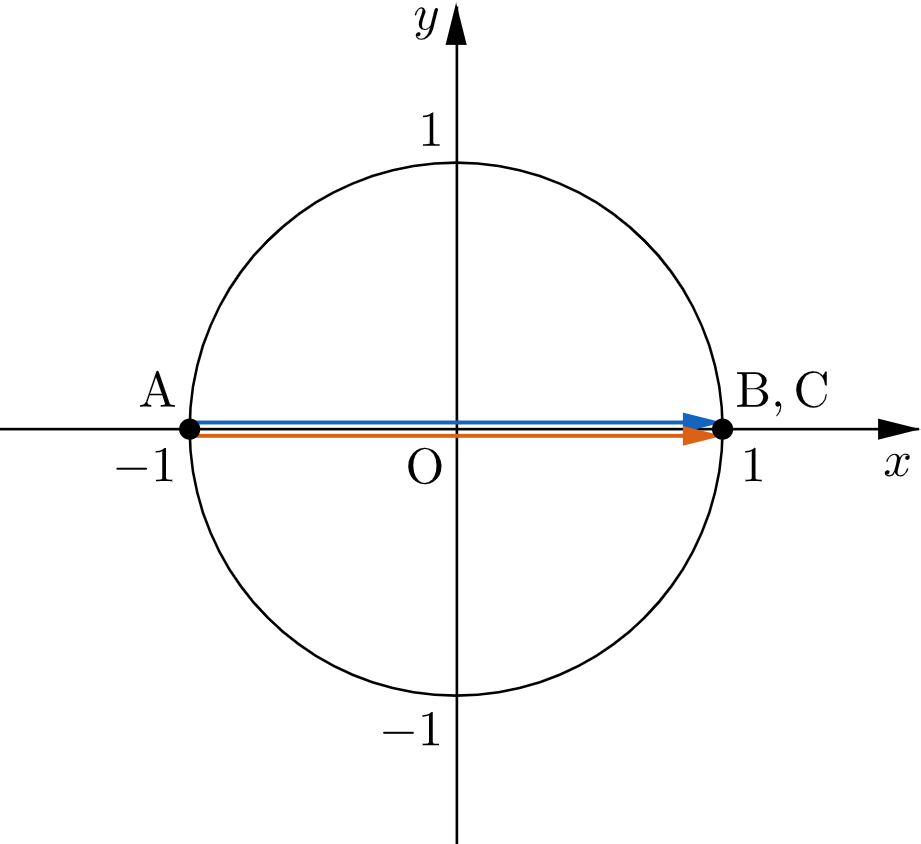
$$\overrightarrow{\mathrm{AB}}\cdot\overrightarrow{\mathrm{AC}}\leqq4$$が必要となるが、$\mathrm{A}(-1,0)$，$\mathrm{B}(1,0)$，$\mathrm{C}(1,0)$ のとき
$$\overrightarrow{\mathrm{AB}}\cdot\overrightarrow{\mathrm{AC}}=
\begin{pmatrix}2 \\[-1pt] 0\end{pmatrix}\cdot\begin{pmatrix}2 \\[-1pt] 0\end{pmatrix}=4$$となるので、$\overrightarrow{\mathrm{AB}}\cdot\overrightarrow{\mathrm{AC}}$ の最大値は $\mathbf{4}$ である。

(ⅱ)　最小値について

対称性より、$0^\circ\leqq\theta\leqq90^\circ$ を満たす $\theta$ を用いて
$$\mathrm{B}(\cos\theta,\,\sin\theta), \ \ \mathrm{C}(\cos\theta,\,-\sin\theta)$$とおける。

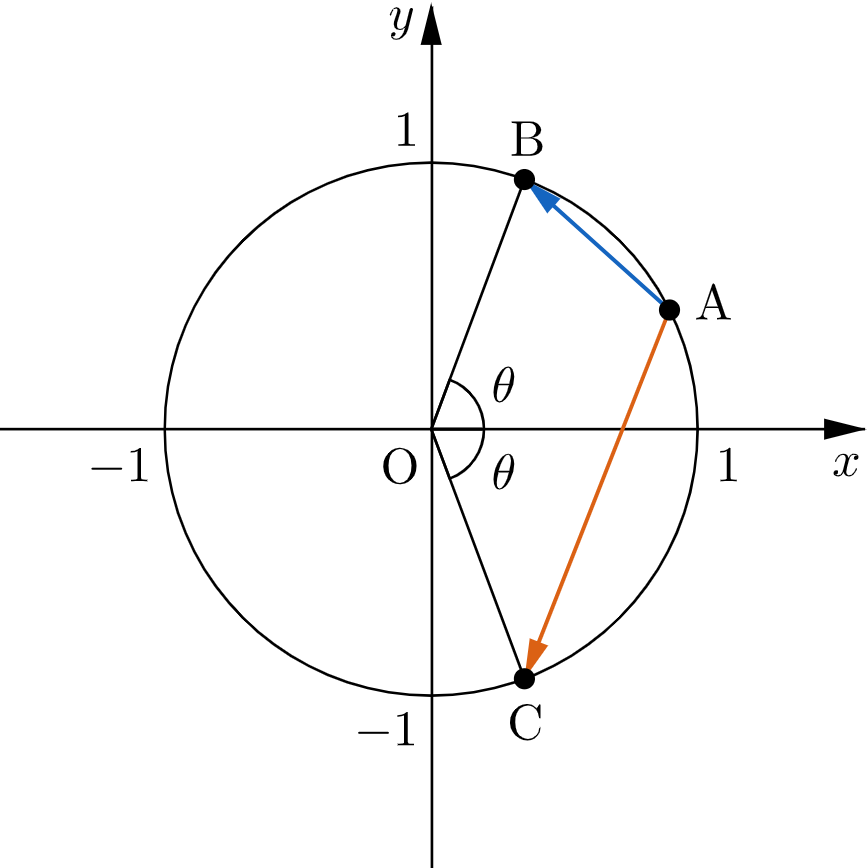
このとき、点 $(-1,0)$ を含む弧 $\mathrm{BC}$ 上に点 $\mathrm{A}$ があるとき、$0^\circ\leqq\angle\mathrm{BAC}\leqq90^\circ$ となるので $\overrightarrow{\mathrm{AB}}\cdot\overrightarrow{\mathrm{AC}}\geqq0$ となる。一方、点 $(1,0)$ を含む弧 $\mathrm{BC}$ 上に点 $\mathrm{A}$ があるとき、$90^\circ\leqq\angle\mathrm{BAC}\leqq180^\circ$ となるので $\overrightarrow{\mathrm{AB}}\cdot\overrightarrow{\mathrm{AC}}\leqq0$ となる。

よって、$\overrightarrow{\mathrm{AB}}\cdot\overrightarrow{\mathrm{AC}}$ の最小値を考える上では、点 $\mathrm{A}$ が点 $(1,0)$ を含む弧 $\mathrm{BC}$ 上にあるときを考えればよい。

このとき、$|\,\overrightarrow{\mathrm{OA}}\,|=|\,\overrightarrow{\mathrm{OB}}\,|=|\,\overrightarrow{\mathrm{OC}}\,|=1$ に注意すると
$$\begin{eqnarray}
&& \overrightarrow{\mathrm{AB}}\cdot\overrightarrow{\mathrm{AC}} \\
&=& (\overrightarrow{\mathrm{OB}}-\overrightarrow{\mathrm{OA}})\cdot(\overrightarrow{\mathrm{OC}}-\overrightarrow{\mathrm{OA}}) \\
&=& \overrightarrow{\mathrm{OB}}\cdot\overrightarrow{\mathrm{OC}}-(\overrightarrow{\mathrm{OA}}\cdot\overrightarrow{\mathrm{OB}}+\overrightarrow{\mathrm{OA}}\cdot\overrightarrow{\mathrm{OC}})+|\,\overrightarrow{\mathrm{OA}}\,|^2 \\[0.3em]
&=& \cos\angle\mathrm{BOC}-(\cos\angle\mathrm{AOB}+\cos\angle\mathrm{AOC})+1 \\[0.3em]
&=& \cos\angle\mathrm{BOC}-2\cos\dfrac{\angle\mathrm{AOB}+\angle\mathrm{AOC}}{2}\cos\dfrac{\angle\mathrm{AOB}-\angle\mathrm{AOC}}{2}+1 \\
&=& \cos2\theta-2\cos\theta\cos\dfrac{\angle\mathrm{AOB}-\angle\mathrm{AOC}}{2}+1.
\end{eqnarray}$$

$\cos\theta\geqq0$ であるから、$\overrightarrow{\mathrm{AB}}\cdot\overrightarrow{\mathrm{AC}}$ が最小となるのは $\cos\dfrac{\angle\mathrm{AOB}-\angle\mathrm{AOC}}{2}$ が最大となるとき、すなわち $\angle\mathrm{AOB}=\angle\mathrm{AOC}$ となるときである。このとき、$\mathrm{A}(1,0)$ である。

したがって
$$\begin{eqnarray}
\overrightarrow{\mathrm{AB}}\cdot\overrightarrow{\mathrm{AC}} &=& \cos2\theta-2\cos\theta+1 \\
&=& 2\cos^2\theta-1-2\cos\theta+1 \\
&=& 2\left(\cos\theta-\dfrac{1}{2}\right)^2-\dfrac{1}{2}
\end{eqnarray}$$であり、$0\leqq\cos\theta\leqq1$ において $\overrightarrow{\mathrm{AB}}\cdot\overrightarrow{\mathrm{AC}}$ は $\cos\theta=\dfrac{1}{2}$（すなわち $\theta=60^\circ\,$）のとき最小値 $\boldsymbol{-\dfrac{1}{2}}$ をとる。

解説

問題文は短いですが、考えがいのある問題です。特に、最小値に関しては予測も簡単ではなく、三角比の計算にどれだけ慣れているかが問われています。

最大値に関しては簡単に予測ができるので、本解答では最大値だけを先に求めました。

最小値に関しては、三角比の和積の公式を用いて、$\angle\mathrm{AOB}$ と $\angle\mathrm{AOC}$ が等しくなければならないことを示しました。後半は $2$ 次関数の最小値に関する問題に帰着します。

なお、$\mathrm{A}(1,0)$，$\mathrm{B}(\cos\alpha,\,\sin\alpha)$，$\mathrm{C}(\cos\beta,\,\sin\beta)$ とおいて、和積の公式を用いてまとめて最大・最小を求める方法もあります。

まとめ

今回は、一橋大学数学（2020年 第3問）の解説をしました。