今回は、東京大学理系数学(2018年 第6問)の解説をしたいと思います。
問題
座標空間内の $4$ 点 $\mathrm{O}(0,0,0), \ $$\mathrm{A}(1,0,0), \ $$\mathrm{B}(1,1,0), \ $$\mathrm{C}(1,1,1)$ を考える。
$\dfrac{1}{2}\lt r\lt1$ とする。点 $\mathrm{P}$ が線分 $\mathrm{OA}, \ $$\mathrm{AB}, \ $$\mathrm{BC}$ 上を動くときに点 $\mathrm{P}$ を中心とする半径 $r$ の球(内部を含む)が通過する部分を,それぞれ $V_1, \ $$V_2, \ $$V_3$ とする。⑴ 平面 $y=t$ が $V_1, \ $$V_3$ 双方と共有点をもつような $t$ の範囲を与えよ。さらに,この範囲の $t$ に対し,平面 $y=t$ と $V_1$ の共通部分および,平面 $y=t$ と $V_3$ の共通部分を同一平面上に図示せよ。
⑵ $V_1$ と $V_3$ の共通部分が $V_2$ に含まれるための $r$ についての条件を求めよ。
⑶ $r$ は⑵の条件をみたすとする。$V_1$ の体積を $S$ とし,$V_1$ と $V_2$ の共通部分の体積を $T$ とする。$V_1, \ $$V_2, \ $$V_3$ を合わせて得られる立体 $V$ の体積を $S$ と $T$ を用いて表せ。
⑷ ひきつづき $r$ は⑵の条件をみたすとする。$S$ と $T$ を求め,$V$ の体積を決定せよ。
(東京大学)
解答
⑴
$V_1$ は $-r\leqq y\leqq r$ の範囲に存在し、$V_3$ は $1-r\leqq y\leqq 1+r$ の範囲に存在する。
$\dfrac{1}{2}\lt r\lt1$ において $1-r\lt r$ であるから、平面 $y=t$ が $V_1, \ $$V_3$ 双方と共有点をもつような $t$ の範囲は
$$\boldsymbol{1-r\leqq t\leqq r}\,.$$
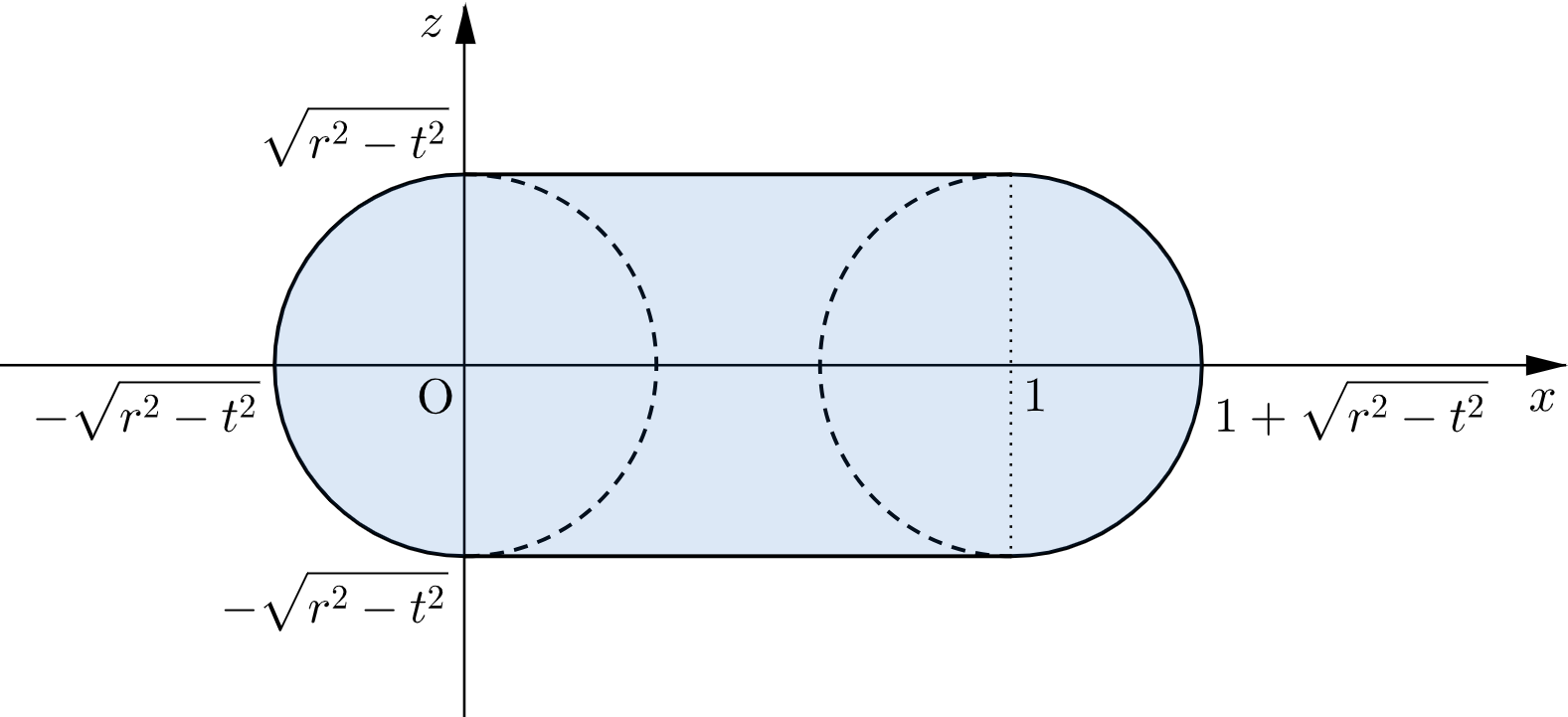
点 $\mathrm{P}$ が線分 $\mathrm{OA}$ 上にあるとき、球と平面 $y=t$ の共通部分は半径 $\sqrt{r^2-t^2}$ の円(内部を含む)となり、その中心は点 $\mathrm{P}$ から平面 $y=t$ に下ろした垂線の足となる。
よって、平面 $y=t$ と $V_1$ の共通部分は下図の網掛け部分のようになる。ただし、境界を含む。
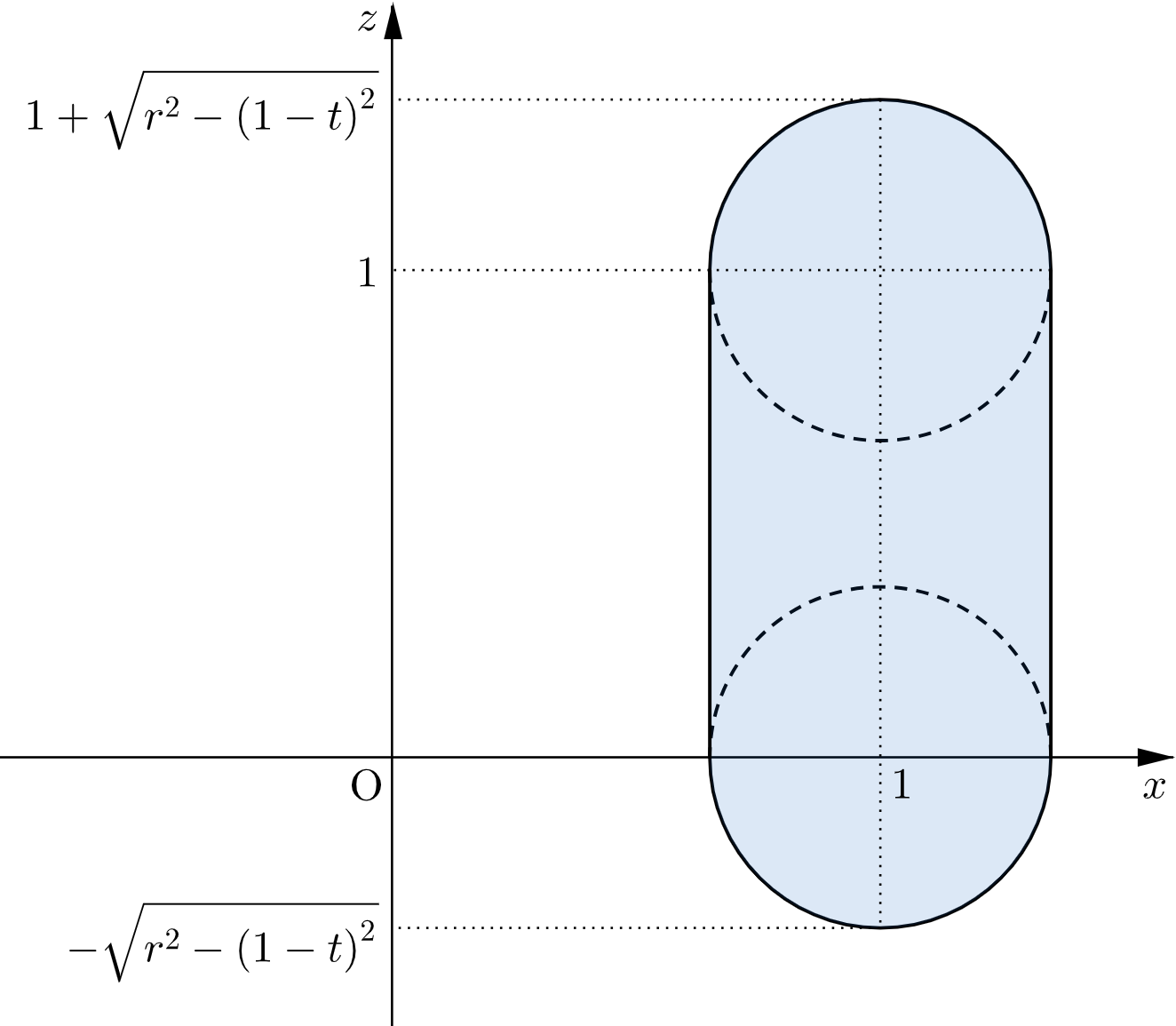
同様に、点 $\mathrm{P}$ が線分 $\mathrm{BC}$ 上にあるとき、球と平面 $y=t$ の共通部分は半径 $\sqrt{r^2-(1-t)^2}$ の円(内部を含む)となり、その中心は点 $\mathrm{P}$ から平面 $y=t$ に下ろした垂線の足となる。
よって、平面 $y=t$ と $V_3$ の共通部分は下図の網掛け部分のようになる。ただし、境界を含む。
ここで、$\sqrt{r^2-t^2}$ と $\sqrt{r^2-(1-t)^2}$ の大小関係について考えると
$$\begin{alignat}{2}
&& \sqrt{r^2-t^2} & \gtreqqless\sqrt{r^2-(1-t)^2} \\[0.2em]
\Longleftrightarrow \ && r^2-t^2 & \gtreqqless r^2-(1-t)^2 \ \text{(}\because(\text{両辺})\gt0\,\text{)} \\[0.3em]
\Longleftrightarrow \ && 0 & \gtreqqless -1+2t \\[0.2em]
\Longleftrightarrow \ && \dfrac{1}{2} & \gtreqqless t \ \text{(複号同順)}
\end{alignat}$$より
$$\left\{\begin{array}{l}
\sqrt{r^2-t^2}\geqq\sqrt{r^2-(1-t)^2}\quad\left(1-r\leqq t\leqq\dfrac{1}{2} \ \text{のとき}\right)\\
\sqrt{r^2-t^2}\leqq\sqrt{r^2-(1-t)^2}\quad\left(\dfrac{1}{2}\leqq t\leqq r \ \text{のとき}\right)
\end{array}\right.$$となる。
したがって、平面 $y=t$ と $V_1$ の共通部分および、平面 $y=t$ と $V_3$ の共通部分を同一平面上に図示すると、下図の網掛け部分のようになる。ただし、境界を含む。
$1-r\leqq t\leqq\dfrac{1}{2}$ のとき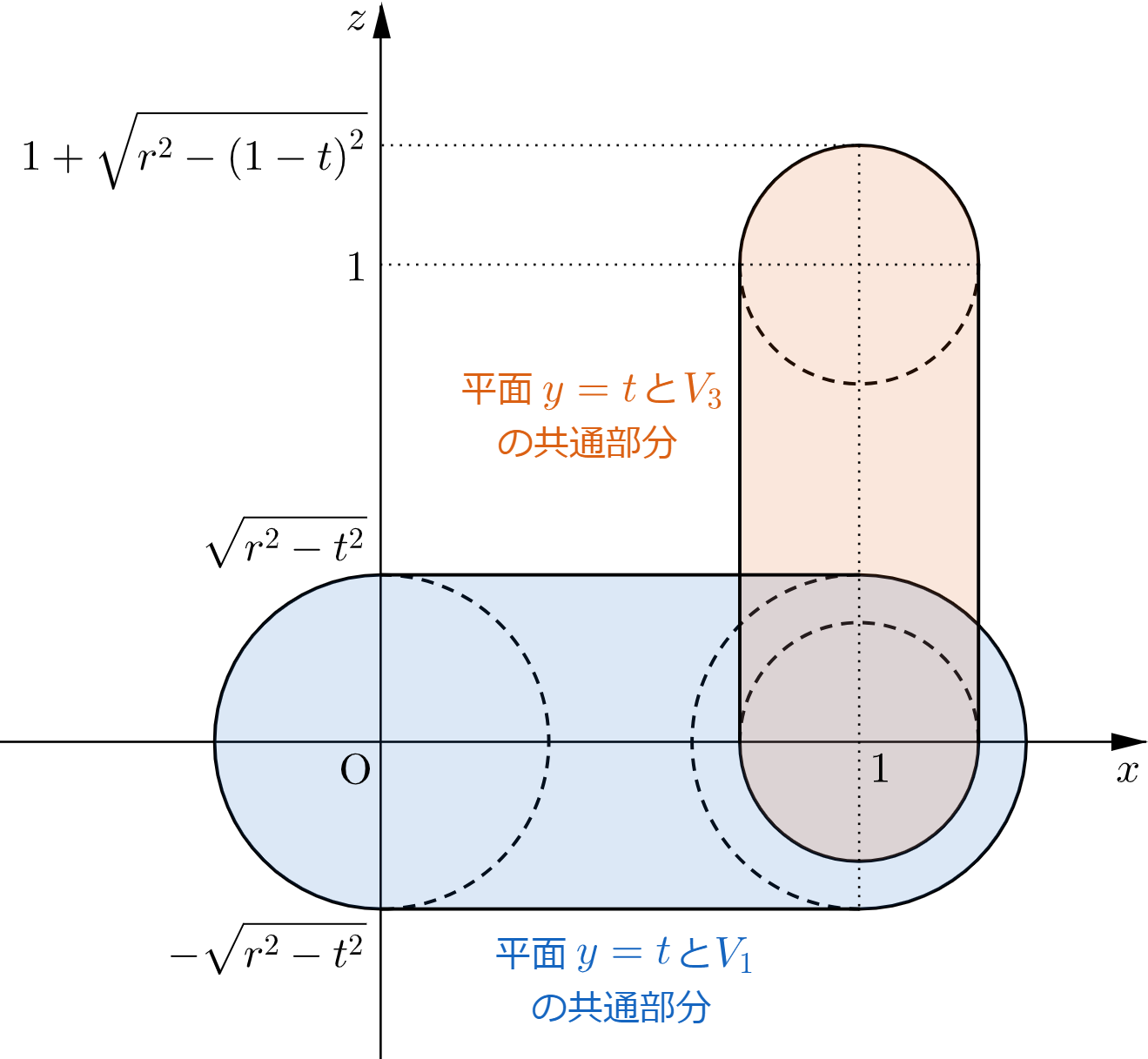
$\dfrac{1}{2}\leqq t\leqq r$ のとき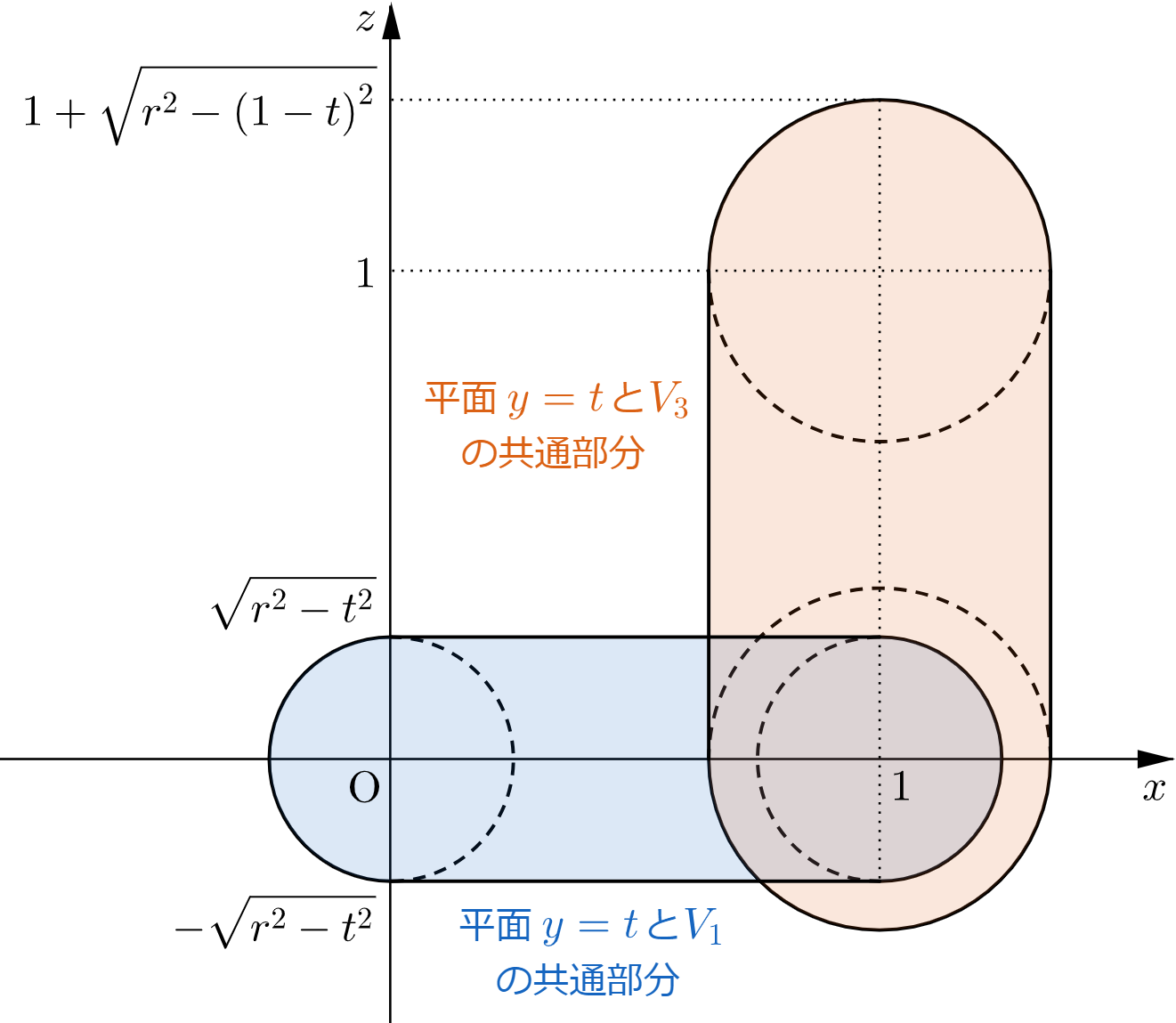
$t$ の範囲:$\boldsymbol{1-r\leqq t\leqq r}$
平面 $y=t$ と $V_1, \ $$V_3$ の共通部分:下図の網掛け部分(境界を含む)
$1-r\leqq t\leqq\dfrac{1}{2}$ のとき
$\dfrac{1}{2}\leqq t\leqq r$ のとき
⑵
⑴より、$V_1$ と $V_3$ の共通部分が存在する $y$ 座標の範囲は $1-r\leqq y\leqq r$ であるから、この範囲において「$V_1$ と $V_3$ の共通部分」の平面 $y=t$ による断面が $V_2$ に含まれればよい。
$1-r\leqq y\leqq r$ において、平面 $y=t$ と $V_2$ の共通部分は中心を $(1,\,t,\,0)$ とする半径 $r$ の円(内部を含む)となる。
「$V_1$ と $V_3$ の共通部分」の平面 $y=t$ による断面の中で、点 $(1,\,t,\,0)$ との距離が最大の点の座標は $(1-\sqrt{r^2-(1-t)^2},\,t,\,\sqrt{r^2-t^2})$ であるから、平面 $y=t$ 上において、$V_1$ と $V_3$ の共通部分が $V_2$ に含まれるための条件は
$$\begin{array}{c}
\begin{aligned}
{\sqrt{r^2-t^2}}^{\,2}+{\sqrt{r^2-(1-t)^2}}^{\,2} &\leqq r^2 \\
r^2-t^2+r^2-(1-t)^2 &\leqq r^2
\end{aligned} \\[0.3em]
\begin{aligned}
\therefore \ r^2 &\leqq 2t^2-2t+1 \\
&= 2\left(t-\dfrac{1}{2}\right)^2+\dfrac{1}{2}. \quad\cdots\text{①}
\end{aligned}
\end{array}$$
$1-r\leqq t\leqq r$ において、$2\left(t-\dfrac{1}{2}\right)^2+\dfrac{1}{2}$ は $t=\dfrac{1}{2}$ のとき最小値 $\dfrac{1}{2}$ をとる。
よって、①が成り立つための $r$ の条件は
$$r^2\leqq\dfrac{1}{2}.$$
$\dfrac{1}{2}\lt r\lt1$ に注意すると、求める $r$ についての条件は
$$\boldsymbol{\dfrac{1}{2}\lt r\leqq\dfrac{1}{\sqrt{2}}}.$$
$$\boldsymbol{\dfrac{1}{2}\lt r\leqq\dfrac{1}{\sqrt{2}}}$$
⑶
立体 $X$ の体積を $|X|$ で表す。
対称性より、$|V_2|=|V_3|=S$ であり、$|V_2\cap V_3|=T$ である。
ここで、条件より $V_1\cap V_3$ は $V_2$ に含まれるので、$|V_1\cap V_2\cap V_3|=|V_1\cap V_3|.$
よって
$$\begin{align}
|V| &= |V_1|+|V_2|+|V_3|-|V_1\cap V_2|-|V_2\cap V_3|-|V_1\cap V_3|+|V_1\cap V_2\cap V_3| \\[0.2em]
&= |V_1|+|V_2|+|V_3|-|V_1\cap V_2|-|V_2\cap V_3| \\[0.2em]
&= \boldsymbol{3S-2T}.
\end{align}$$
$$\boldsymbol{3S-2T}$$
⑷
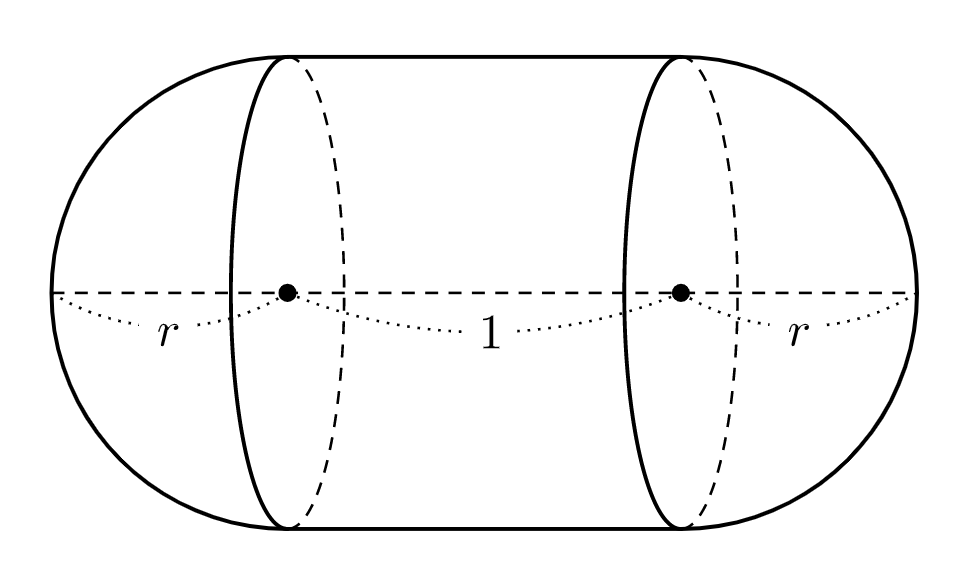
$V_1$ は、半径 $r$ の半球 $2$ つと、底面の半径が $r$,高さが $1$ の円柱を合わせたものなので
$$\begin{align}
S &= \dfrac{4}{3}\pi r^3\cdot\dfrac{1}{2}\cdot 2+\pi r^2\cdot 1 \\
&= \boldsymbol{\dfrac{4}{3}\pi r^3+\pi r^2}.
\end{align}$$
$k$ を $-r\leqq k\leqq r$ を満たす実数とし、$V_1\cap V_2$ の平面 $z=k$ による断面を図示すると、下図の網掛け部分のようになる。ただし、境界を含む。
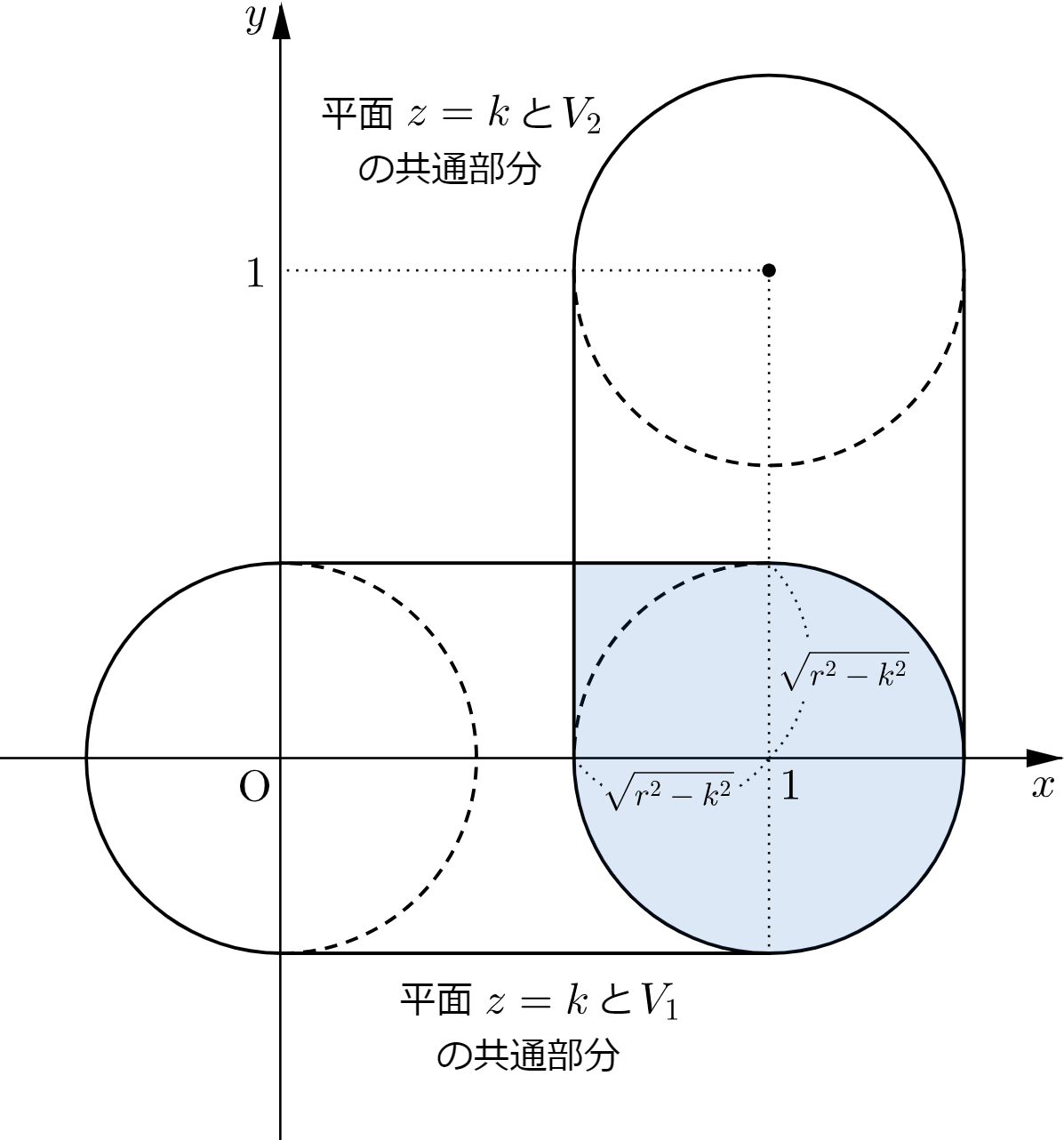
この断面の面積は
$$\begin{eqnarray}
&& \dfrac{3}{4}\pi{\sqrt{r^2-k^2}}^2+{\sqrt{r^2-k^2}}^2 \\
&=& \left(\dfrac{3}{4}\pi+1\right)(r^2-k^2).
\end{eqnarray}$$
よって
$$\begin{align}
T &= \displaystyle\int_{-r}^{r}\left(\dfrac{3}{4}\pi+1\right)(r^2-k^2)\,dk \\
&= 2\left(\dfrac{3}{4}\pi+1\right)\displaystyle\int_{0}^{r}(r^2-k^2)\,dk \\
&= \left(\dfrac{3}{2}\pi+2\right)\left[r^2k-\dfrac{k^3}{3}\right]_0^r \\
&= \boldsymbol{\left(\pi+\dfrac{4}{3}\right)r^3}.
\end{align}$$
したがって、$V$ の体積は
$$\begin{align}
|V| &= 3S-2T \\
&= 3\left(\dfrac{4}{3}\pi r^3+\pi r^2\right)-2\left(\pi+\dfrac{4}{3}\right)r^3 \\
&= \boldsymbol{\left(2\pi-\dfrac{8}{3}\right)r^3+3\pi r^2}.
\end{align}$$
$$\begin{array}{l}
S=\boldsymbol{\dfrac{4}{3}\pi r^3+\pi r^2}, \ \ T=\boldsymbol{\left(\pi+\dfrac{4}{3}\right)r^3}, \\[0.2em]
V \ \text{の体積は} \ \boldsymbol{\left(2\pi-\dfrac{8}{3}\right)r^3+3\pi r^2}
\end{array}$$
解説
問題設定はシンプルですが、状況を空間的に把握しようとすると混乱しがちです。空間図形を把握するコツは平面による断面や $1$ 方向から見た図形を考えることなので、小問も平面的に考えるよう誘導しています。
特に⑶では、空間的にパズルを解こうとすると難しいので、集合の考え方を用いてシンプルに解くことがポイントです。異なる分野の考え方をすぐに引き出せれるよう練習しておきましょう。
⑷の $T$ を求める問題では、どの軸に垂直に切れば断面積が容易に求められるかを考える必要があります。
まとめ
今回は、東京大学理系数学(2018年 第6問)の解説をしました。
ほかの問題にもチャレンジしよう!
東京大学 理系数学 2018年 第1問 解説
東京大学 理系数学 2018年 第2問 解説
東京大学 理系数学 2018年 第3問 解説
東京大学 理系数学 2018年 第4問 解説
東京大学 理系数学 2018年 第5問 解説
東京大学 理系数学 2018年 第6問 解説













