東京大学 理系数学 2019年 第2問 解説

今回は、東京大学理系数学（2019年 第2問）の解説をしたいと思います。

問題

　一辺の長さが $1$ の正方形 $\mathrm{ABCD}$ を考える。$3$ 点 $\mathrm{P},\,$$\mathrm{Q},\,$$\mathrm{R}$ はそれぞれ辺 $\mathrm{AB},\,$$\mathrm{AD},\,$$\mathrm{CD}$ 上にあり，$3$ 点 $\mathrm{A},\,$$\mathrm{P},\,$$\mathrm{Q}$ および $3$ 点 $\mathrm{P},\,$$\mathrm{Q},\,$$\mathrm{R}$ はどちらも面積が $\dfrac{1}{3}$ の三角形の $3$ 頂点であるとする。

　$\dfrac{\mathrm{DR}}{\mathrm{AQ}}$ の最大値，最小値を求めよ。

（東京大学）

解答

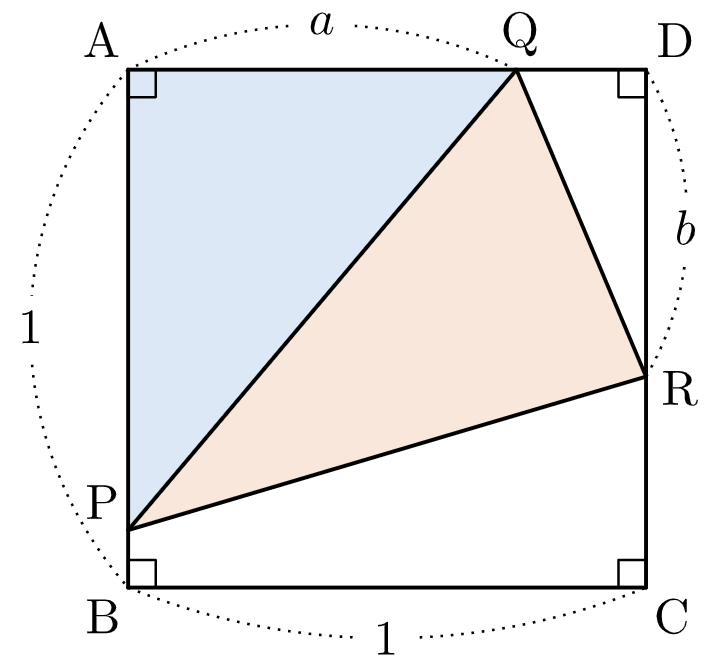
$\mathrm{AQ}=a$，$\mathrm{DR}=b$ とおくと
$$0\lt a\leqq1 \ \cdots\text{①},\quad 0\leqq b\leqq1. \ \cdots\text{②}$$

$(\triangle\mathrm{APQ} \ \text{の面積})=\dfrac{1}{3}$ より
$$\begin{align}
\dfrac{1}{2}\cdot a\cdot\mathrm{AP} &= \dfrac{1}{3} \\
\therefore \ \mathrm{AP} &= \dfrac{2}{3a} \ \text{（}\because\text{①より} \ a\ne0\,\text{）}
\end{align}$$であり、$0\lt \mathrm{AP}\leqq1$ より
$$0\lt\dfrac{2}{3a}\leqq1 \ \Longleftrightarrow \ a\geqq\dfrac{2}{3}. \ \cdots\text{③}$$

条件より、正方形 $\mathrm{ABCD}$ から $\triangle\mathrm{APQ}$ と $\triangle\mathrm{PQR}$ を引いた部分、すなわち台形 $\mathrm{PBCR}$（点 $\mathrm{P}$ が点 $\mathrm{B}$ に一致するときは $\triangle\mathrm{BCR}\,$）と $\triangle\mathrm{DQR}$ を合わせた部分の面積は $1-\dfrac{1}{3}-\dfrac{1}{3}=\dfrac{1}{3}$ であるから
$$\begin{array}{c}
\left(1-\dfrac{2}{3a}+1-b\right)\cdot1\cdot\dfrac{1}{2}+\dfrac{1}{2}(1-a)b=\dfrac{1}{3} \\
\begin{align}
\left(6-\dfrac{2}{a}-3b\right)+3(1-a)b &= 2 \\
4-\dfrac{2}{a}-3ab &= 0.
\end{align}
\end{array}$$①より $a\ne0$ であるから
$$b=\dfrac{4a-2}{3a^2}.$$

②より
$$\begin{align}
&\hphantom{\Longleftrightarrow} \quad \ 0\leqq\dfrac{4a-2}{3a^2}\leqq1 \\[0.3em]
&\Longleftrightarrow \ \left\{\begin{array}{l}
0\leqq4a-2 \\
4a-2\leqq3a^2
\end{array}\right. \\[0.3em]
&\Longleftrightarrow \ \left\{\begin{array}{l}
a\geqq\dfrac{1}{2} \\
3\left(a-\dfrac{2}{3}\right)^2+\dfrac{2}{3}\geqq0
\end{array}\right. \\[0.3em]
&\Longleftrightarrow \quad a\geqq\dfrac{1}{2}. \quad\cdots\text{④}
\end{align}$$

①,③,④より、$a$ の範囲は
$$\dfrac{2}{3}\leqq a\leqq1. \quad\cdots\text{⑤}$$

ここで
$$\dfrac{\mathrm{DR}}{\mathrm{AQ}}=\dfrac{b}{a}=\dfrac{4}{3a^2}-\dfrac{2}{3a^3}$$であり
$$f(a)=\dfrac{4}{3a^2}-\dfrac{2}{3a^3}$$ とおくと
$$f'(a)=-\dfrac{8}{3a^3}+\dfrac{2}{a^4}=\dfrac{2}{a^4}\left(1-\dfrac{4}{3}a\right)$$となるから、⑤の範囲における $f(a)$ の増減表は次のようになる。
$$\begin{array}{c|c|c|c|c|c} \hline
a & \dfrac{2}{3} & \cdots & \dfrac{3}{4} & \cdots & 1 \\ \hline
f'(a) & & + & 0 & – & \\ \hline
f(a) & \dfrac{3}{4} & \nearrow & \dfrac{64}{81} & \searrow & \dfrac{2}{3} \\ \hline
\end{array}$$

以上より、求める最大値は $\boldsymbol{\dfrac{64}{81}}$，最小値は $\boldsymbol{\dfrac{2}{3}}$ である。

解説

設定自体は難しくないのでとっつきやすい問題だと思いますが、$a$ の範囲に注意しなければ答えまでたどり着けません。

本解答は幾何を用いて解きましたが、例えば点 $\mathrm{A}$ を原点に重なるようにして、座標平面で解く解法も有効です。

その場合、$\triangle\mathrm{PQR}$ の面積を $3$ 頂点の座標を用いて直接表せるのがメリットです。

まとめ

今回は、東京大学理系数学（2019年 第2問）の解説をしました。