今回は、東京大学理系数学(2018年 第4問)の解説をしたいと思います。
問題
$a\gt0$ とし,
$$f(x)=x^3-3a^2x$$とおく。次の $2$ 条件をみたす点 $(a,\,b)$ の動きうる範囲を求め,座標平面上に図示せよ。条件1:方程式 $f(x)=b$ は相異なる $3$ 実数解をもつ。
条件2:さらに,方程式 $f(x)=b$ の解を $\alpha\lt\beta\lt\gamma$ とすると $\beta\gt1$ である。
(東京大学)
解答
$$f'(x)=3x^2-3a^2=3(x+a)(x-a)$$より、$f(x)$ の増減表は次のようになる。
$$\begin{array}{c|c|c|c|c|c} \hline
x & \cdots & -a & \cdots & a & \cdots \\ \hline
f'(x) & + & 0 & – & 0 & + \\ \hline
f(x) & \nearrow & 2a^3 & \searrow & -2a^3 & \nearrow \\ \hline
\end{array}$$
よって、$y=f(x)$ の概形は下図のようになる。
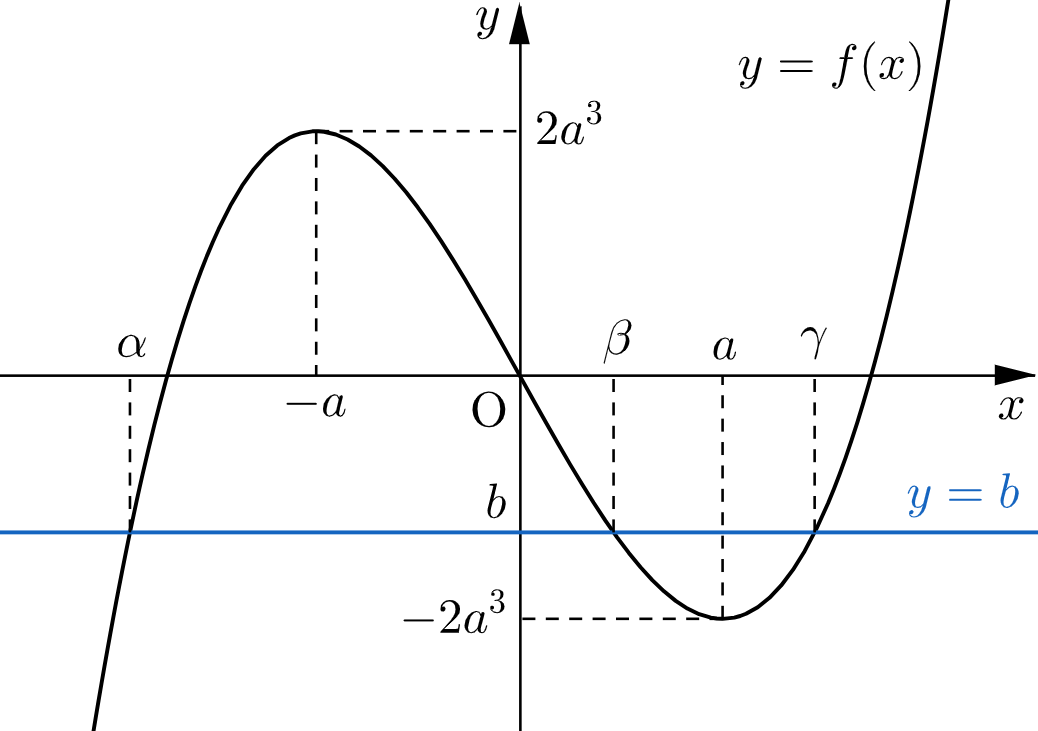
$\alpha,\,\beta,\,\gamma$ は曲線 $y=f(x)$ と直線 $y=b$ の共有点の $x$ 座標であるから、図より、条件1は
$$-2a^3\lt b\lt2a^3 \quad\cdots\text{①}$$と同値であり、このとき条件2は
$$1\lt\beta\lt a \quad\cdots\text{②}$$となる。
増減表より、$1\leqq x\leqq a$ において $f(x)$ は単調減少なので
$$\begin{align}
\text{②} \ &\Longleftrightarrow \ f(a)\lt f(\beta)\lt f(1) \\[0.3em]
&\Longleftrightarrow \ -2a^3\lt b\lt1-3a^2. \quad\cdots\text{③}
\end{align}$$
$a\gt1$ において $1-3a^2\lt0\lt2a^3$ であることに注意すると、①,②,③より、題意を満たす $(a,\,b)$ の条件は
$$\boldsymbol{a\gt1} \ \,\mathbf{\text{かつ}} \, \boldsymbol{-2a^3\lt b\lt1-3a^2}.$$
これを座標平面上に図示すると、下図の網掛け部分のようになる。ただし、境界は含まない。
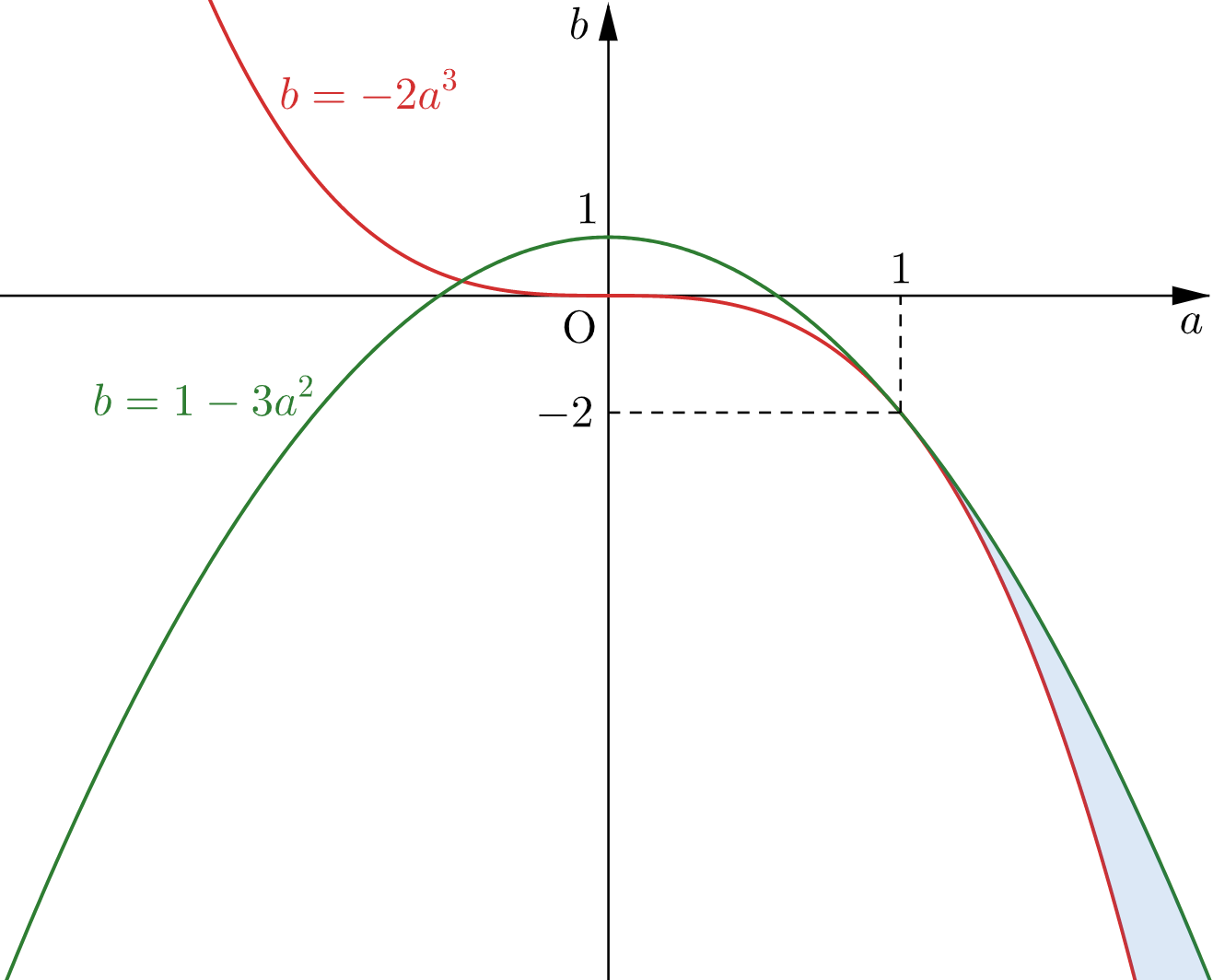
$$\boldsymbol{a\gt1} \ \,\mathbf{\text{かつ}} \, \boldsymbol{-2a^3\lt b\lt1-3a^2}$$
点 $(a,\,b)$ の動きうる範囲は下図の網掛け部分(境界は含まない)

解説
方程式の解が $2$ 曲線(直線)の共有点の $x$ 座標を表すことに注意すれば、答えだけは求められると思います。
この問題のポイントはその答えが $2$ 条件と必要十分であることを論証することです。
本解答はいきなり必要十分条件を示しましたが、必要条件から絞っていく方法も有効です(例えば $2$ 条件を満たすとき $b\lt0$ が必要、など)。
解答の図で、何となく囲まれた部分を塗りたくなりますが、$a\gt1$ に注意しましょう。
まとめ
今回は、東京大学理系数学(2018年 第4問)の解説をしました。
ほかの問題にもチャレンジしよう!
東京大学 理系数学 2018年 第1問 解説
東京大学 理系数学 2018年 第2問 解説
東京大学 理系数学 2018年 第3問 解説
東京大学 理系数学 2018年 第4問 解説
東京大学 理系数学 2018年 第5問 解説
東京大学 理系数学 2018年 第6問 解説













