京都大学 理系数学 2021年 第5問 解説

今回は、京都大学理系数学（2021年 第5問）の解説をしたいと思います。

問題

　$xy$ 平面において，$2$ 点 $\mathrm{B}(-\sqrt{3},-1), \ $$\mathrm{C}(\sqrt{3},-1)$ に対し，点 $\mathrm{A}$ は次の条件 $(*)$ を満たすとする．

$(*)$　$\angle\mathrm{BAC}=\dfrac{\pi}{3}$ かつ点 $\mathrm{A}$ の $y$ 座標は正．

　次の各問に答えよ．

⑴　$\triangle\mathrm{ABC}$ の外心の座標を求めよ．

⑵　点 $\mathrm{A}$ が条件 $(*)$ を満たしながら動くとき，$\triangle\mathrm{ABC}$ の垂心の軌跡を求めよ．

（京都大学）

解答

⑴

解法1

点 $\mathrm{A}$ が $y$ 軸上にあるとき
$$\mathrm{AB}=\mathrm{AC},\quad \angle\mathrm{BAC}=\dfrac{\pi}{3}$$より $\triangle\mathrm{ABC}$ は $y$ 軸に対称な正三角形となる。

この正三角形の $1$ 辺の長さは $2\sqrt{3}$ なので、高さは
$$2\sqrt{3}\times\dfrac{1}{2}\times\tan\dfrac{\pi}{3}=3$$となり、点 $\mathrm{A}$ の $y$ 座標が正であるから、点 $\mathrm{A}$ の座標は $(0,2)$ となる。

正三角形の外心は重心と一致するので、外心の座標は原点である。

点 $\mathrm{A}$ が条件 $(*)$ を満たすとき、円周角の定理の逆より、この外接円の $y\gt 0$ の部分を動く。

よって、$\triangle\mathrm{ABC}$ の外心の座標は $\boldsymbol{(0,0)}$ である。

解法2

$\triangle\mathrm{ABC}$ の外心を $\mathrm{D}$ とすると、$\mathrm{D}$ は線分 $\mathrm{BC}$ の垂直二等分線である $y$ 軸上に存在する。

円周角と中心角の関係から
$$\angle\mathrm{BDC}=2\angle\mathrm{BAC}=\dfrac{2}{3}\pi$$

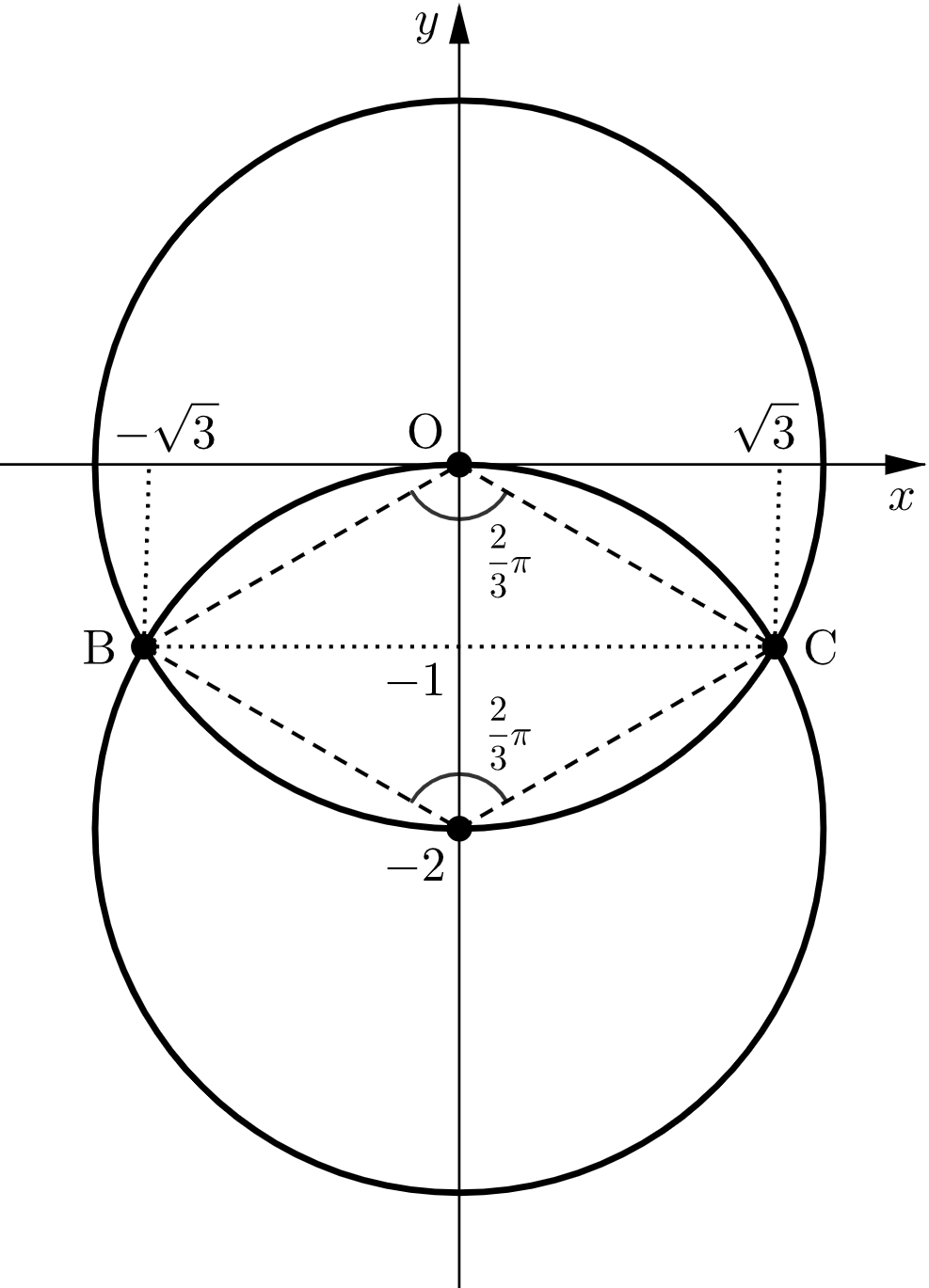
よって、$\triangle\mathrm{ABC}$ の外心の座標は $\boldsymbol{(0,0)}$ である。

⑵

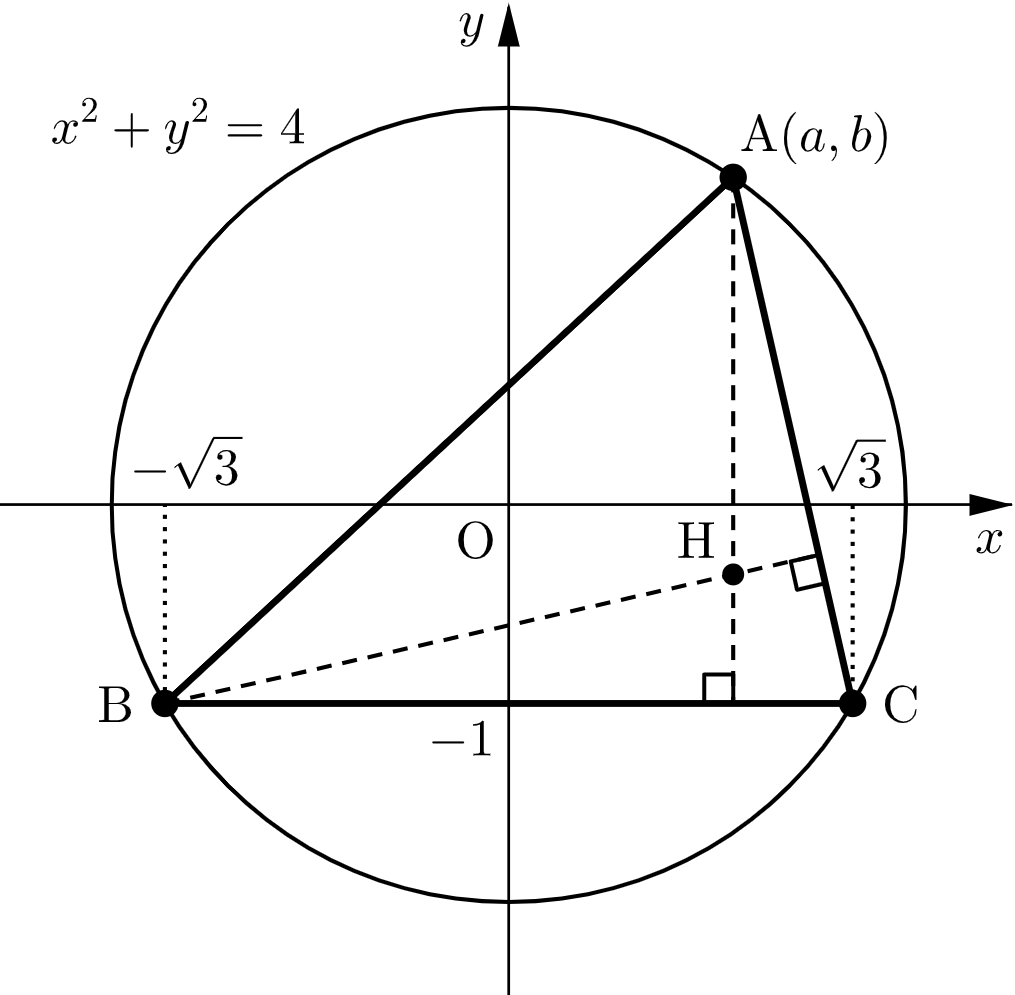
点 $\mathrm{A}$ の座標を $(a,b)$ とおく。

原点を $\mathrm{O}$ とすると、$\mathrm{OB}=2$ なので、$\triangle\mathrm{ABC}$ の外接円は原点を中心とする半径 $2$ の円となる。

したがって、$a,b$ は
$$\begin{eqnarray}
a^2+b^2 &=& 4 \quad\cdots\text{①}, \\
b &\gt& 0 \quad\cdots\text{②}
\end{eqnarray}$$を満たす。

解法1（2直線の交点）

$a\ne \sqrt{3}$ のとき、直線 $\mathrm{AC}$ の方程式は
$$y=\dfrac{b+1}{a-\sqrt{3}}(x-\sqrt{3})-1$$なので、$\mathrm{B}$ から直線 $\mathrm{AC}$ に下ろした垂線の方程式は
$$y=-\dfrac{a-\sqrt{3}}{b+1}(x+\sqrt{3})-1 \quad\cdots\text{③}$$となる。またこの垂線の方程式は $a=\sqrt{3}$ のときも成り立つ。

$\mathrm{A}$ から直線 $\mathrm{BC}$ に下ろした垂線の方程式は $x=a$ なので、③より $\triangle\mathrm{ABC}$ の垂心の $y$ 座標は
$$\begin{eqnarray}
y &=& -\dfrac{a-\sqrt{3}}{b+1}(a+\sqrt{3})-1 \\
&=& \dfrac{-a^2+3-(b+1)}{b+1} \\
&=& \dfrac{-(4-b^2)-b+2}{b+1} \ \text{（}\because\text{①）} \\
&=& \dfrac{(b-2)(b+1)}{b+1} \\
&=& b-2
\end{eqnarray}$$

よって、$\triangle\mathrm{ABC}$ の垂心の座標を $(X,Y)$ とおくと
$$X=a,\quad Y=b-2$$が成り立ち、これより
$$a=X,\quad b=Y+2$$を①,②に代入すると
$$X^2+(Y+2)^2=4,\quad Y+2\gt 0$$

したがって、求める垂心の軌跡は
$$\boldsymbol{\mathbf{円} \ x^2+(y+2)^2=4 \ \mathbf{の} \ y\gt -2 \ \mathbf{を満たす部分}}$$

解法2（ベクトル）

$\triangle\mathrm{ABC}$ の垂心を $\mathrm{H}$ とし、その座標を $(X,Y)$ とおく。

$\mathrm{H}$ は $\mathrm{A}$ から直線 $\mathrm{BC}$ に下ろした垂線上の点なので
$$X=a \quad\cdots\text{④}$$

また、$\mathrm{CA}\perp\mathrm{BH}$ より
$$\begin{eqnarray}
\overrightarrow{\mathrm{CA}}\cdot \overrightarrow{\mathrm{BH}} &=& 0 \\
(a-\sqrt{3}, \ b+1)\cdot(X+\sqrt{3}, \ Y+1) &=& 0 \\
(a-\sqrt{3})(X+\sqrt{3})+(b+1)(Y+1) &=& 0 \\
(a-\sqrt{3})(a+\sqrt{3})+(b+1)(Y+1) &=& 0 \ \text{（}\because\text{④）}
\end{eqnarray}$$$$\begin{eqnarray}
(b+1)(Y+1) &=& 3-a^2 \\
&=& 3-(4-b^2) \ \text{（}\because\text{①）} \\
&=& (b+1)(b-1)
\end{eqnarray}$$②より $b+1 \ne 0$ なので
$$\begin{eqnarray}
Y+1 &=& b-1 \\[0.5em]
\therefore\quad Y &=& b-2
\end{eqnarray}$$

よって、$a=X, \ b=Y+2$ を①,②に代入すると
$$X^2+(Y+2)^2=4,\quad Y+2\gt 0$$

したがって、求める垂心の軌跡は
$$\boldsymbol{\mathbf{円} \ x^2+(y+2)^2=4 \ \mathbf{の} \ y\gt -2 \ \mathbf{を満たす部分}}$$

解説

⑴は答えだけならすぐ思いつきますが、説明に迷うかもしれません。

「解法1」のように特殊な場合から円周角の定理の逆を使うか、「解法2」のように円周角と中心角の関係から外心の候補を絞りましょう。

⑵は垂心と点 $\mathrm{A}$ の $x$ 座標が同じであるという、言われてみれば当たり前のことに気付けるかが意外とポイントです。

また、最初から $\mathrm{A}(a,\sqrt{4-a^2})$ とおくのは計算が複雑になるのでオススメしません。

まとめ

今回は、京都大学理系数学（2021年 第5問）の解説をしました。