神戸大学 理系数学 2020年 第2問 解説

今回は、神戸大学理系数学（2020年 第2問）の解説をしたいと思います。

問題

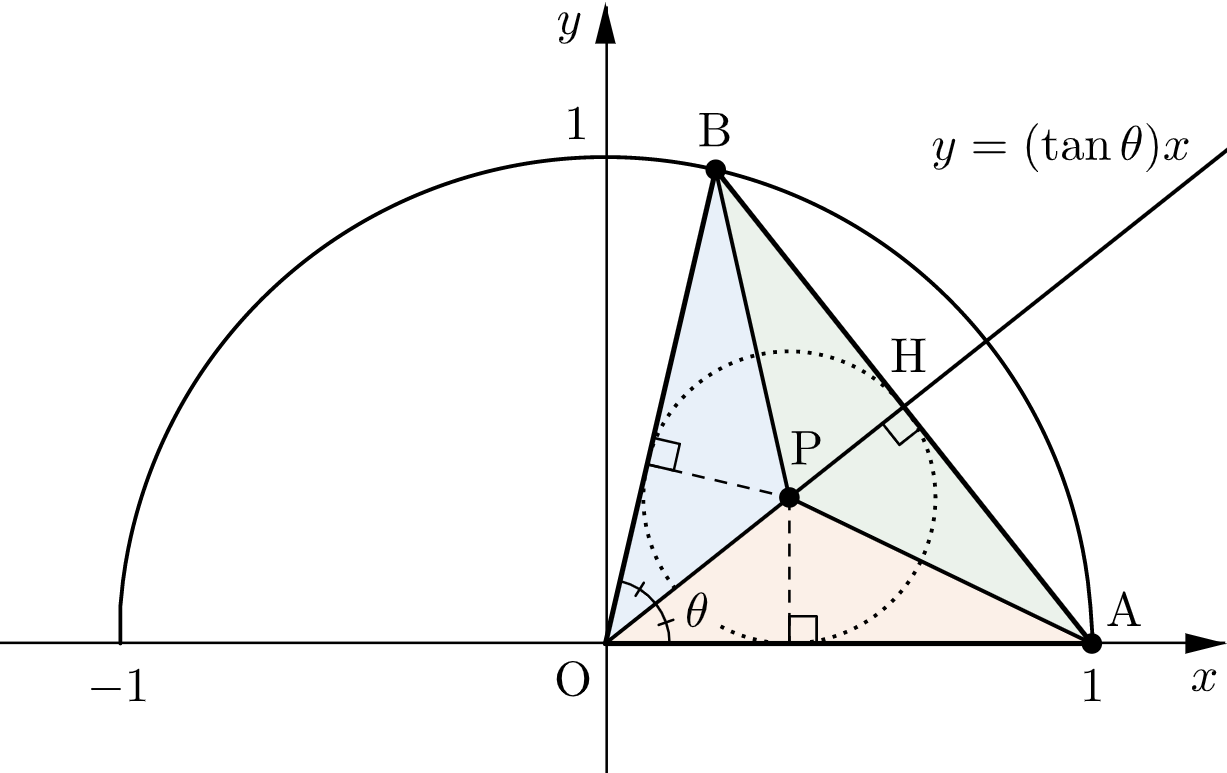
$\theta$ を $0\lt\theta\lt\dfrac{\pi}{2}$ をみたす実数とし，原点 $\mathrm{O}, \ $$\mathrm{A}(1,0), \ $$\mathrm{B}(\cos 2\theta,\sin 2\theta)$ を頂点とする $\triangle\mathrm{OAB}$ の内接円の中心を $\mathrm{P}$ とする．また，$\theta$ がこの範囲を動くときに点 $\mathrm{P}$ が描く曲線と線分 $\mathrm{OA}$ によって囲まれた部分を $D$ とする．以下の問に答えよ．

⑴　点 $\mathrm{P}$ の座標は $\left(1-\sin\theta,\dfrac{\sin\theta\cos\theta}{1+\sin\theta}\right)$ で表されることを示せ．

⑵　$D$ を $x$ 軸のまわりに $1$ 回転させてできる立体の体積を求めよ．

（神戸大学）

解答

⑴

点 $\mathrm{B}$ は原点を中心とする半径 $1$ の円の $y\gt 0$ の部分に存在するので、$\triangle\mathrm{OAB}$ は $\mathrm{OA}=\mathrm{OB}$ の二等辺三角形である。

よって、$\mathrm{O}$ から直線 $\mathrm{AB}$ に下ろした垂線の足を $\mathrm{H}$ とすると
$$\begin{align}
\mathrm{AB} &= 2\mathrm{AH} \\
&= 2\mathrm{OA}\sin\angle\mathrm{AOH} \\
&= 2\sin\theta
\end{align}$$となる。

ここで、$\triangle\mathrm{OAB}$ の面積に関して
$$\triangle\mathrm{OAB}=\triangle\mathrm{OAP}+\triangle\mathrm{OBP}+\triangle\mathrm{ABP}$$が成り立つので、$\triangle\mathrm{OAB}$ の内接円の半径を $r$ とすると
$$\begin{align}
\dfrac{1}{2}\cdot 1\cdot 1\cdot\sin 2\theta &= \dfrac{1}{2}\cdot(1+1+2\sin\theta)\cdot r \\
\sin 2\theta &= 2(1+\sin\theta)r
\end{align}$$となる。

$0\lt\theta\lt\dfrac{\pi}{2}$ より $1+\sin\theta\ne 0$ なので
$$\begin{align}
r &= \dfrac{\sin 2\theta}{2(1+\sin\theta)} \\
&= \dfrac{2\sin\theta\cos\theta}{2(1+\sin\theta)} \\
&= \dfrac{\sin\theta\cos\theta}{1+\sin\theta}
\end{align}$$となる。これは点 $\mathrm{P}$ の $y$ 座標に等しい。

また、点 $\mathrm{P}$ は $\triangle\mathrm{OAB}$ の内心なので、$\angle\mathrm{AOB}$ の二等分線上に存在する。

この二等分線の方程式は
$$y=(\tan\theta)x$$である。

$0\lt\theta\lt\dfrac{\pi}{2}$ において $\tan\theta\ne 0$ であるから、点 $\mathrm{P}$ の $x$ 座標は
$$\begin{align}
\dfrac{1}{\tan\theta}\cdot\dfrac{\sin\theta\cos\theta}{1+\sin\theta}
&= \dfrac{\cos^2\theta}{1+\sin\theta} \\
&= \dfrac{1-\sin^2\theta}{1+\sin\theta} \\
&= \dfrac{(1+\sin\theta)(1-\sin\theta)}{1+\sin\theta} \\
&= 1-\sin\theta
\end{align}$$となる。

以上より、点 $\mathrm{P}$ の座標は $\left(1-\sin\theta,\dfrac{\sin\theta\cos\theta}{1+\sin\theta}\right)$ で表される。$$\tag{証明終}$$

⑵

$$x(\theta)=1-\sin\theta,\quad y(\theta)=\dfrac{\sin\theta\cos\theta}{1+\sin\theta}$$とおく。

$$x'(\theta)=-\cos\theta\lt 0 \quad \left(\because 0\lt\theta\lt\dfrac{\pi}{2}\right)$$より、$x(\theta)$ は単調減少する。

また、明らかに点 $\mathrm{P}$ は $y\gt 0$ の部分に存在し
$$\begin{align}
\displaystyle\lim_{\theta\to 0+0}(x(\theta),y(\theta)) &= (1,0), \\[0.3em]
\displaystyle\lim_{\theta\to\frac{\pi}{2}-0}(x(\theta),y(\theta)) &= (0,0)
\end{align}$$であるから、求める体積 $V$ は
$$\begin{align}
V &= \displaystyle\int_0^1\pi y^2dx \\
&= \pi\displaystyle\int_{\frac{\pi}{2}}^0\{y(\theta)\}^2\dfrac{dx(\theta)}{d\theta}d\theta \\
&= \pi\displaystyle\int_0^{\frac{\pi}{2}}\dfrac{\sin^2\theta\cos^2\theta}{(1+\sin\theta)^2}\cdot\cos\theta \ d\theta \\
&= \pi\displaystyle\int_0^{\frac{\pi}{2}}\dfrac{\sin^2\theta(1+\sin\theta)(1-\sin\theta)}{(1+\sin\theta)^2}\cdot\cos\theta \ d\theta \\
&= \pi\displaystyle\int_0^{\frac{\pi}{2}}\dfrac{\sin^2\theta(1-\sin\theta)}{1+\sin\theta}\cdot\cos\theta \ d\theta \\
&= \pi\displaystyle\int_0^{\frac{\pi}{2}}\left(-\sin^2\theta+2\sin\theta-2+\dfrac{2}{1+\sin\theta}\right)\cos\theta \ d\theta \\
&= \pi\left[-\dfrac{\sin^3\theta}{3}+\sin^2\theta-2\sin\theta+2\log|1+\sin\theta|\right]_0^{\frac{\pi}{2}} \\
&= \boldsymbol{\pi\left(2\log 2-\dfrac{4}{3}\right)}
\end{align}$$

解説

⑴は、内心の性質を上手く使うことがポイントです。

角の二等分線どうしの交点の座標から求める方法もありますが、計算量が多くなるので、本解答では面積を使った解法としました。

⑵は、立式までは簡単だと思いますが、積分を解くのは難しいです。
大量の $\sin$ と $1$ つだけの $\cos$ がつくれたら、合成関数の微分を利用するチャンスなので、見逃さないようにしましょう。

まとめ

今回は、神戸大学理系数学（2020年 第2問）の解説をしました。