今回は、神戸大学理系数学(2019年 第5問)の解説をしたいと思います。
問題
媒介変数表示
$$x=\sin t,\quad y=(1+\cos t)\sin t\quad(0\leqq t\leqq\pi)$$で表される曲線を $C$ とする.以下の問に答えよ.⑴ $\dfrac{dy}{dx}$ および $\dfrac{d^2y}{dx^2}$ を $t$ の関数として表せ.
⑵ $C$ の凹凸を調べ,$C$ の概形を描け.
⑶ $C$ で囲まれる領域の面積 $S$ を求めよ.
(神戸大学)
解答
⑴
$$\begin{align}
\dfrac{dx}{dt} &= \cos t, \\[0.3em]
\dfrac{dy}{dt} &= (-\sin t)\sin t+(1+\cos t)\cos t \\
&= 2\cos^2t+\cos t-1
\end{align}$$より、$t\ne\dfrac{\pi}{2}$ において
$$\dfrac{dy}{dx}=\boldsymbol{\dfrac{2\cos^2t+\cos t-1}{\cos t}}$$
また
$$\begin{align}
\dfrac{d^2y}{dx^2} &= \dfrac{d}{dt}\left(\dfrac{dy}{dx}\right)\cdot\dfrac{dt}{dx} \\
&= \dfrac{\{4\cos t(-\sin t)-\sin t\}\cos t-(2\cos^2t+\cos t-1)(-\sin t)}{\cos^2t}\cdot\dfrac{1}{\cos t} \\
&= \boldsymbol{-\dfrac{(2\cos^2t+1)\sin t}{\cos^3t}}
\end{align}$$
$$\begin{array}{l}
\dfrac{dy}{dx}=\boldsymbol{\dfrac{2\cos^2t+\cos t-1}{\cos t}}, \\[0.3em]
\dfrac{d^2y}{dx^2}=\boldsymbol{-\dfrac{(2\cos^2t+1)\sin t}{\cos^3t}}
\end{array}$$
⑵
$$\dfrac{dy}{dx}=\dfrac{(2\cos t-1)(\cos t+1)}{\cos t}$$である。
また、$0\lt t\lt\pi$ において
$$2\cos^2t+1\gt 0,\quad\sin t\gt 0$$ より、$\dfrac{d^2y}{dx^2}$ の符号は $\cos t$ の符号に依存する。
よって、増減表は次のようになる。
$$\begin{array}{c||c|c|c|c|c|c|c}\hline
t & 0 & \cdots & \dfrac{\pi}{3} & \cdots & \dfrac{\pi}{2} & \cdots & \pi \\ \hline
\dfrac{dx}{dt} & & + & + & + & 0 & – & \\ \hline
x & 0 & \nearrow & \dfrac{\sqrt{3}}{2} & \nearrow & 1 & \searrow & 0 \\ \hline
\dfrac{dy}{dt} & & + & 0 & – & – & – & \\ \hline
y & 0 & \nearrow & \dfrac{3\sqrt{3}}{4} & \searrow & 1 & \searrow & 0 \\ \hline
\dfrac{dy}{dx} & & + & 0 & – & & + & \\ \hline
\dfrac{d^2y}{dx^2} & & – & – & – & & + & \\ \hline
(x,y) & & \text{上に凸} & \text{極大} & \text{上に凸} & \text{変曲点} & \text{下に凸} & \\ \hline
\end{array}$$
以上より、$C$ の凹凸については、$\boldsymbol{0\lt t\lt\dfrac{\pi}{2}}$ のとき上に凸、$\boldsymbol{\dfrac{\pi}{2}\lt t\lt\pi}$ のとき下に凸である。
また、$C$ の概形は下図のようになる。
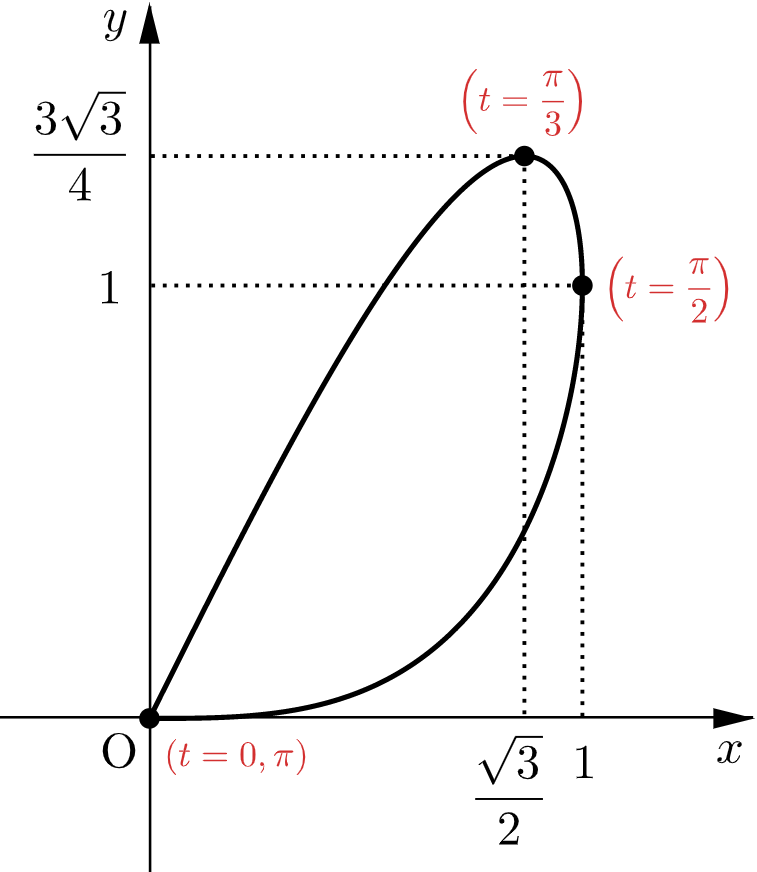
$\boldsymbol{0\lt t\lt\dfrac{\pi}{2}}$ のとき上に凸、$\boldsymbol{\dfrac{\pi}{2}\lt t\lt\pi}$ のとき下に凸

⑶
$$y=\left\{
\begin{array}{ll}
y_1 & \left(0\leqq t\leqq\dfrac{\pi}{2} \ \text{のとき}\right) \\
y_2 & \left(\dfrac{\pi}{2}\leqq t\leqq\pi \ \text{のとき}\right) \\
\end{array}
\right.$$とおくと
$$\begin{align}
S &= \displaystyle\int_{0}^{1}y_1dx-\displaystyle\int_{0}^{1}y_2dx \\
&= \displaystyle\int_{0}^{\frac{\pi}{2}}y\dfrac{dx}{dt}dt-\displaystyle\int_{\pi}^{\frac{\pi}{2}}y\dfrac{dx}{dt}dt \\
&= \displaystyle\int_{0}^{\pi}y\dfrac{dx}{dt}dt \\
&= \displaystyle\int_{0}^{\pi}(1+\cos t)\sin t\cos t \ dt \\
&= -\displaystyle\int_{0}^{\pi}(\cos t+\cos^2t)(\cos t)’dt \\
&= -\left[\dfrac{\cos^2t}{2}+\dfrac{\cos^3t}{3}\right]_{0}^{\pi} \\
&= \boldsymbol{\dfrac{2}{3}}
\end{align}$$
$$\boldsymbol{\dfrac{2}{3}}$$
解説
⑴は、$\dfrac{d^2y}{dx^2}\ne\dfrac{\dfrac{d^2y}{dt^2}}{\dfrac{d^2x}{dt^2}}$ に注意しましょう。
⑵は、$\dfrac{dy}{dx}$ と $\dfrac{d^2y}{dx^2}$ の関係を的確に捉えて概形に落とし込みましょう。
⑶は、いきなり $S=\displaystyle\int_{0}^{\pi}y\dfrac{dx}{dt}dt$ から始めてはいけません。面積の差をとった結果、媒介変数がつながったという過程を見せましょう。
まとめ
今回は、神戸大学理系数学(2019年 第5問)の解説をしました。
ほかの問題にもチャレンジしよう!
神戸大学 理系数学 2019年 第1問 解説
神戸大学 理系数学 2019年 第2問 解説
神戸大学 理系数学 2019年 第3問 解説
神戸大学 理系数学 2019年 第4問 解説
神戸大学 理系数学 2019年 第5問 解説













