一橋大学 数学 2022年[後期] 第5問 解説

今回は、一橋大学数学（2022年後期 第5問）の解説をしたいと思います。

問題

　次の [Ⅰ]，[Ⅱ] のいずれか一方を選択して解答せよ。

[Ⅰ]　$t$ を実数とする。直線 $x=t$ に関して曲線 $C_1:y=x^3-2x^2-4x$ と対称な曲線を $C_2$ とする。

⑴　$C_1$ と $C_2$ が共有点をちょうど $3$ 個持つときの $t$ の範囲を求めよ。

⑵　$t$ が⑴の範囲を動くとき，$C_1$ と $C_2$ で囲まれた $2$ つの部分の面積の和を $S(t)$ とする。$S(t)$ の最大値を求めよ。

[Ⅱ]　$x\gt0$ に対して
$$(1+x)^{\frac{1}{x}}\lt e\lt(1+x)^{\frac{1}{x}+1}$$が成り立つことを示せ。

（一橋大学）

解答

[Ⅰ]

⑴

$x$ 座標が $p,\,q$ である $2$ 点が直線 $x=t$ に関して対称であるとき
$$\dfrac{p+q}{2}=t \ \Longleftrightarrow \ q=2t-p$$が成り立つので、$C_2$ の式は $C_1$ の式で $x$ を $2t-x$ とすることによって
$$y=(2t-x)^3-2(2t-x)^2-4(2t-x)$$と求められる。

$C_1$ と $C_2$ の式から $y$ を消去すると
$$\begin{array}{c}
x^3-2x^2-4x=(2t-x)^3-2(2t-x)^2-4(2t-x) \\[0.3em]
\begin{align}
0 &= x^3-(2t-x)^3-2\{x^2-(2t-x)^2\}-4\{x-(2t-x)\} \\[0.2em]
&= \{x-(2t-x)\}\{x^2+x(2t-x)+(2t-x)^2\} \\
&\hphantom{=} \ \ -2\{x-(2t-x)\}\{x+(2t-x)\}-4\{x-(2t-x)\} \\[0.2em]
&= 2(x-t)(x^2-2tx+4t^2)-2\cdot2(x-t)\cdot2t-4\cdot2(x-t) \\[0.3em]
\therefore \ 0 &= (x-t)(x^2-2tx+4t^2-4t-4) \quad\cdots\text{①}
\end{align}
\end{array}$$となり、①の解が $C_1$ と $C_2$ の共有点の $x$ 座標を表す。

$$f(x)=x^2-2tx+4t^2-4t-4$$とおくと、題意を満たすための必要十分条件は
$$\left\{\begin{alignat}{2}
&f(x)=0 \ \text{が異なる} \ 2 \ \text{つの実数解をもつ}& &\quad\cdots\text{②} \\
&f(x)=0 \ \text{が} \ x=t \ \text{を解にもたない}& &\quad\cdots\text{③}
\end{alignat}\right.$$である。

②より、$(\,f(x)=0$ の判別式$\,)\gt0$ なので
$$\begin{array}{c}
\begin{align}
t^2-(4t^2-4t-4) &\gt 0 \\
3t^2-4t-4 &\lt 0 \\
(3t+2)(t-2) &\lt 0
\end{align} \\
\therefore \ -\dfrac{2}{3}\lt t\lt2 \quad\cdots\text{④}
\end{array}$$

③より、$f(t)\ne0$ なので
$$\begin{array}{c}
\begin{align}
t^2-2t^2+4t^2-4t-4 &\ne 0 \\
3t^2-4t-4 &\ne 0 \\
(3t+2)(t-2) &\ne 0
\end{align} \\
\therefore \ t\ne-\dfrac{2}{3},\,2 \quad\cdots\text{⑤}
\end{array}$$

④,⑤より、求める $t$ の範囲は
$$\boldsymbol{-\dfrac{2}{3}\lt t\lt2} \quad\cdots\text{⑥}$$

⑵

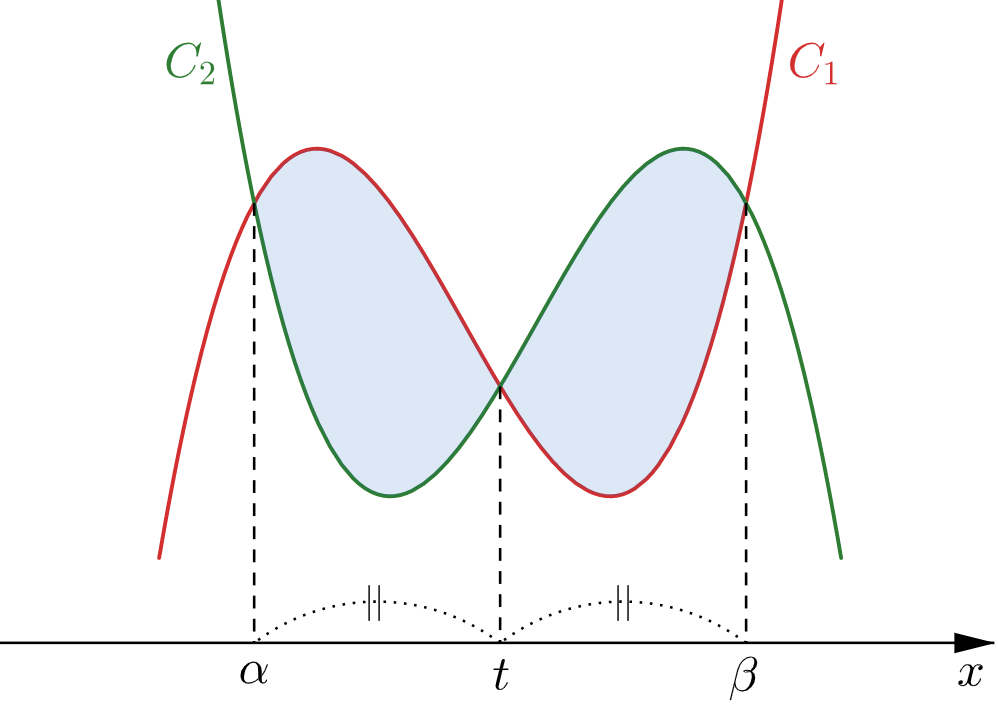
$f(x)=0$ の解を $\alpha,\,$$\beta$$\text{（}\,\alpha\lt\beta\,\text{）}$とすると、①の解は $x=t,\,\alpha,\,\beta$ であり
$$\begin{align}
\alpha &= t-\sqrt{-3t^2+4t+4}=t-\sqrt{-f(t)}\,, \\
\beta &= t+\sqrt{-3t^2+4t+4}=t+\sqrt{-f(t)}
\end{align}$$より $\alpha\lt t\lt\beta$ となる。

また
$$\begin{align}
f(x) &= (x-t)^2+3t^2-4t-4 \\
&= (x-t)^2+f(t)
\end{align}$$が成り立つ。

よって
$$\begin{align}
S(t) &= \displaystyle\int_{\alpha}^{t}[x^3-2x^2-4x-\{(2t-x)^3-2(2t-x)^2-4(2t-x)\}]dx \\
&\hphantom{=} \ +\displaystyle\int_{t}^{\beta}[\{(2t-x)^3-2(2t-x)^2-4(2t-x)\}-(x^3-2x^2-4x)]dx \\
&= \displaystyle\int_{\alpha}^{t}2(x-t)f(x)dx-\displaystyle\int_{t}^{\beta}2(x-t)f(x)dx \\[0.5em]
\dfrac{S(t)}{2} &= \displaystyle\int_{\alpha}^{t}(x-t)\{(x-t)^2+f(t)\}dx-\displaystyle\int_{t}^{\beta}(x-t)\{(x-t)^2+f(t)\}dx \\
&= \displaystyle\int_{\alpha}^{t}\{(x-t)^3+f(t)(x-t)\}dx-\displaystyle\int_{t}^{\beta}\{(x-t)^3+f(t)(x-t)\}dx \\
&= \left[\dfrac{(x-t)^4}{4}+f(t)\cdot\dfrac{(x-t)^2}{2}\right]_{\alpha}^{t}-\left[\dfrac{(x-t)^4}{4}+f(t)\cdot\dfrac{(x-t)^2}{2}\right]_{t}^{\beta} \\
&= -\dfrac{(\alpha-t)^4}{4}-f(t)\cdot\dfrac{(\alpha-t)^2}{2}-\dfrac{(\beta-t)^4}{4}-f(t)\cdot\dfrac{(\beta-t)^2}{2} \\
&= -\dfrac{\left\{-\sqrt{-f(t)}\right\}^4}{4}-f(t)\cdot\dfrac{\left\{-\sqrt{-f(t)}\right\}^2}{2} \\
&\hphantom{=} \ \ -\dfrac{{\sqrt{-f(t)}}^4}{4}-f(t)\cdot\dfrac{{\sqrt{-f(t)}}^2}{2} \\[0.2em]
&= -\dfrac{\{f(t)\}^2}{4}+\dfrac{\{f(t)\}^2}{2}-\dfrac{\{f(t)\}^2}{4}+\dfrac{\{f(t)\}^2}{2} \\[0.2em]
&= \dfrac{\{f(t)\}^2}{2}
\end{align}$$

したがって
$$\begin{align}
S(t) &= \{f(t)\}^2 \\[0.2em]
&= (3t^2-4t-4)^2 \\
&= \left\{3\left(t-\dfrac{2}{3}\right)^2-\dfrac{16}{3}\right\}^2
\end{align}$$となる。

⑥の範囲において
$$-\dfrac{16}{3}\leqq3\left(t-\dfrac{2}{3}\right)^2-\dfrac{16}{3}\lt0$$より
$$0\lt S(t)\leqq\left(\dfrac{16}{3}\right)^2=\dfrac{256}{9}$$となるから、$S(t)$ の最大値は $\boldsymbol{\dfrac{256}{9}}$ である。

[Ⅱ]

$x\gt0$ において、与式を同値変形すると
$$\begin{align}
\dfrac{\log(1+x)}{x} &\lt 1\lt\left(\dfrac{1}{x}+1\right)\log(1+x) \\[0.3em]
\log(1+x) &\lt x\lt(1+x)\log(1+x) \quad\cdots(*)
\end{align}$$となるので、$(*)$ を示せばよい。

$f(x)=x-\log(1+x)$ とおくと、$x\gt0$ において
$$f'(x)=1-\dfrac{1}{1+x}=\dfrac{x}{1+x}\gt0$$より
$$f(x)\gt f(0)=0-\log1=0$$となるので
$$\log(1+x)\lt x \quad\cdots\text{①}$$が成り立つ。

また、$g(x)=(1+x)\log(1+x)-x$ とおくと、$x\gt0$ において
$$\begin{align}
g'(x) &= \log(1+x)+1+x\cdot\dfrac{1}{1+x}-1 \\
&= \log(1+x)\gt0
\end{align}$$より
$$g(x)\gt g(0)=1\cdot\log1-0=0$$となるので
$$x\lt(1+x)\log(1+x) \quad\cdots\text{②}$$が成り立つ。

①,②より $(*)$ が成り立つため、題意は示された。$$\tag{証明終}$$

解説

[Ⅰ]

曲線と方程式、積分、$2$ 次関数の最大・最小という幅広い分野にまたがった問題で、高度な計算力が必要となります。
（これを文系に出すのかと恐ろしくなりました。）

⑴で、共有点の $x$ 座標を求める際、$x=t$ を解に持つ（$\,(x-t)\,$でくくれる）ことが自明なので、因数分解に時間をとられないようにしましょう。

⑵は、いかに計算量を減らすかがカギです。
まず、$C_1$ と $C_2$ の差を考えるときに、$2(x-t)f(x)$ の係数 $2$ を忘れないようにしましょう。

次に、$f(x)$ が入ったまま積分を計算してもできますが、計算量が膨大になります。そこで、「積分して $x=t$ を代入したときに $0$ となる項を多くしたい」という考えから、
$$f(x)=(x-t)^2+3t^2-4t-4$$と $(x-t)$ を無理矢理つくります。

この変形の良いところは、$(x-t)$ をつくれることだけではありません。
残りの $3t^2-4t-4$ の部分に $x$ が入っていないので、$x$ に関する積分の際に定数と見なせるということです。

以上の工夫をすると、比較的スムーズに（これでも多いですが）積分することができ、あとは $2$ 次関数の最大・最小問題に帰着できます。

[Ⅱ]

数Ⅲが使える人にとっては基本的な問題で、対数・微分に関する基本的な考え方が分かっているかを問う問題です。

示すべき不等式を同値変形し、単調増加性と $f(0)=g(0)=0$ を用いて示しましょう。

まとめ

今回は、一橋大学数学（2022年後期 第5問）の解説をしました。