京都大学 理系数学 2020年 第6問 解説

今回は、京都大学理系数学（2020年 第6問）の解説をしたいと思います。

問題

　$x,y,z$ を座標とする空間において，$xz$ 平面内の曲線
$$z=\sqrt{\log(1+x)}\quad\text{（}\,0\leqq x\leqq1\,\text{）}$$を $z$ 軸のまわりに $1$ 回転させるとき，この曲線が通過した部分よりなる図形を $S$ とする．この $S$ をさらに $x$ 軸のまわりに $1$ 回転させるとき，$S$ が通過した部分よりなる立体を $V$ とする．このとき，$V$ の体積を求めよ．

（京都大学）

解答

$0\lt x\lt1$ において
$$\dfrac{dz}{dx}=\dfrac{1}{2\sqrt{\log(1+x)}}\cdot\dfrac{1}{1+x}\gt0$$より $z=\sqrt{\log(1+x)}$ は単調増加であり、さらに連続なので、$xz$ 平面内において途切れない曲線となっている。

$t$ を $0\leqq t\leqq1$ を満たす実数とし、平面 $x=t$ による $S$ の切り口を $L$ とする。

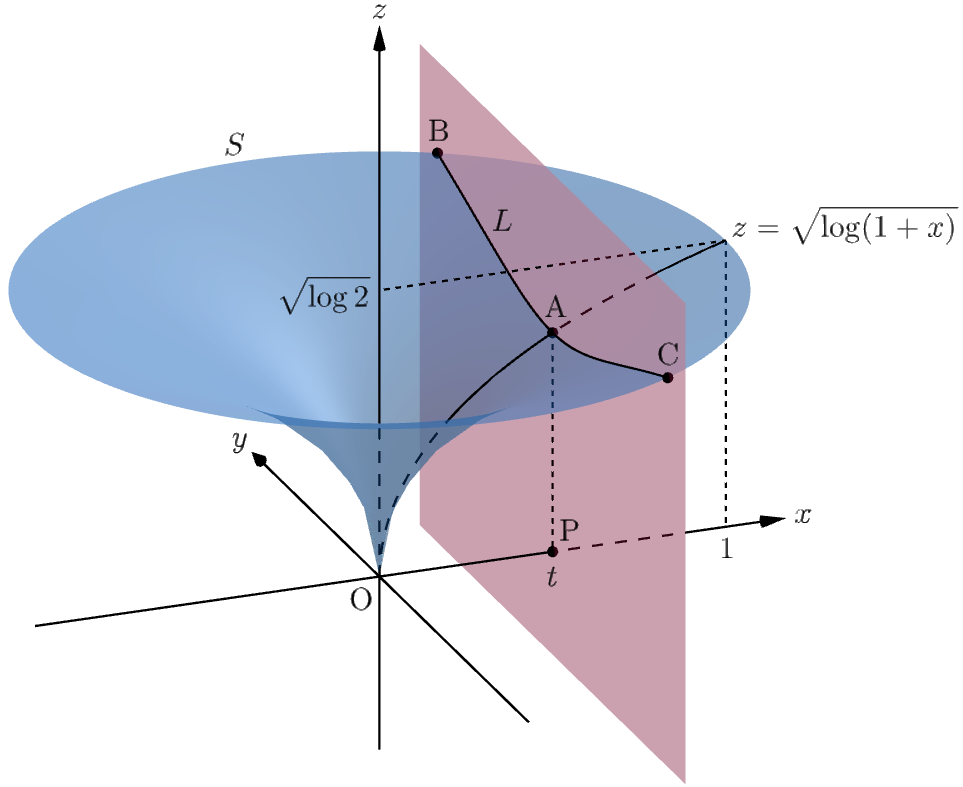
$L$ の $y=0$ における点を $\mathrm{A}$，端点のうち $y$ 座標が正の点を $\mathrm{B}$，負の点を $\mathrm{C}$ とする。

また、$\mathrm{P}(t,0,0)$ とする。

先の議論により、$L$ 上で $\mathrm{P}$ からの距離が最小の点は $\mathrm{A}$，最大の点は $\mathrm{B},\mathrm{C}$ であり、$L$ は途切れない曲線となる。

点 $\mathrm{A}$ の座標は $\big(t,0,\sqrt{\log(1+t)}\big)$ となる。

点 $\mathrm{B},\mathrm{C}$ の座標は、これらが円 $x^2+y^2=1, \ z=\sqrt{\log2}$ 上の点であることに注意すると $\mathrm{B}\big(t,\sqrt{1-t^2},\sqrt{\log2}\big)$，$\mathrm{C}\big(t,-\sqrt{1-t^2},\sqrt{\log2}\big)$ となる。

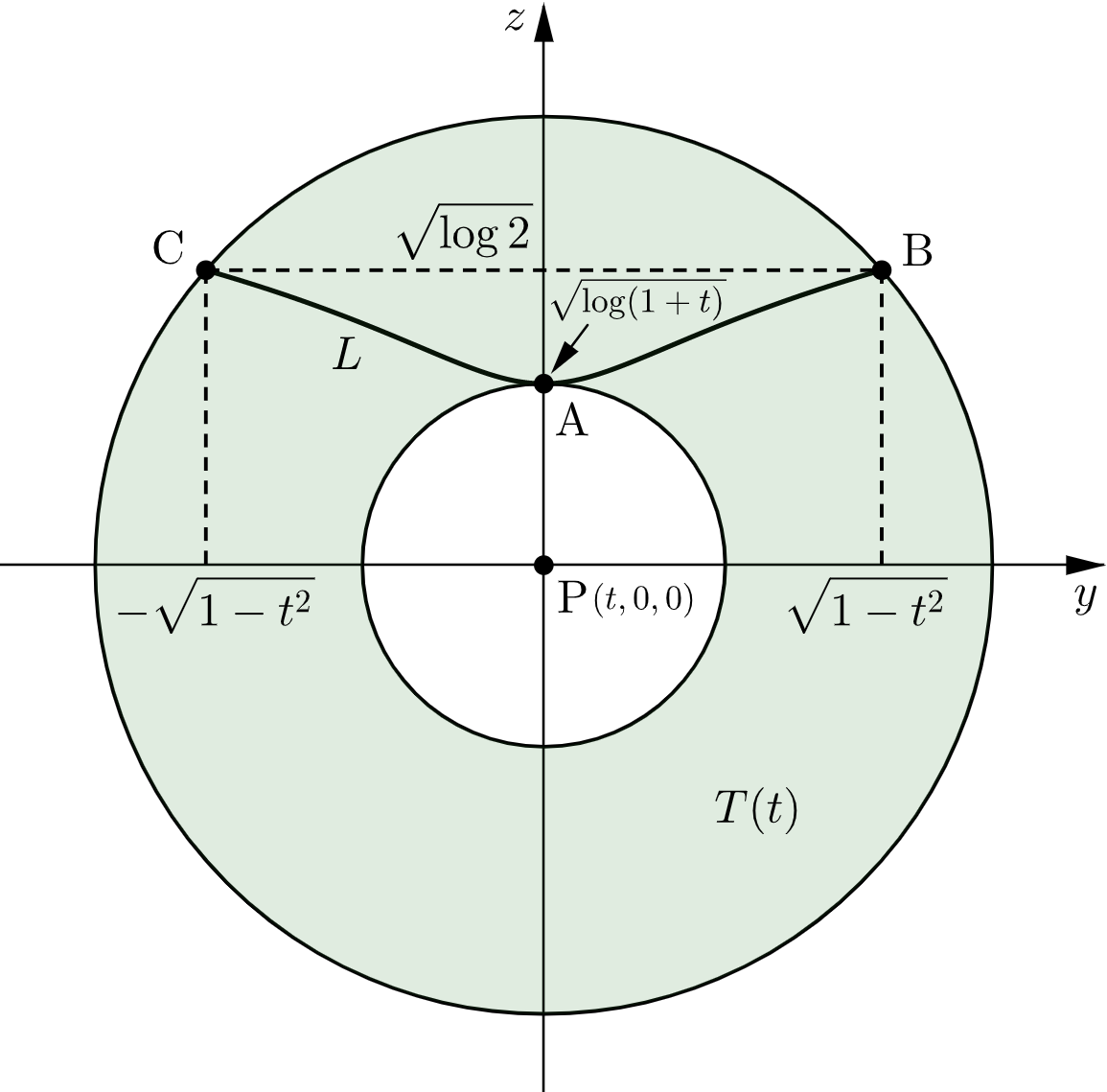
したがって、$L$ を $x$ 軸のまわりに $1$ 回転させたときに通過する部分の面積を $T(t)$ とすると
$$\begin{align}
T(t) &= \pi\mathrm{BP}^2-\pi\mathrm{AP}^2 \\
&= \pi\left\{\sqrt{1-t^2}^2+\sqrt{\log2}^2-\sqrt{\log(1+t)}^2\right\} \\[0.2em]
&= \pi\{1+\log2-t^2-\log(1+t)\}
\end{align}$$

$S$ は平面 $x=0$ に関して対称なので、$V$ も平面 $x=0$ に関して対称となる。

よって、求める体積を $W$ とすると
$$\begin{align}
W &= 2\displaystyle\int_{0}^{1}T(t)dt \\
&= 2\pi\displaystyle\int_{0}^{1}\{1+\log2-t^2-\log(1+t)\}dt \\
&= 2\pi\left[(1+\log2)t-\dfrac{t^3}{3}-(1+t)\log(1+t)+t\right]_{0}^{1} \\
&= 2\pi\left(1+\log2-\dfrac{1}{3}-2\log2+1\right) \\[0.2em]
&= \boldsymbol{\left(\dfrac{10}{3}-2\log2\right)\pi}
\end{align}$$

解説

「回転体の体積は、回転軸に垂直な断面で切ったときの切り口の断面積を考える」という原則どおり解き進めれば、特に難しいところはありません。

体積を求めるときの積分範囲を $-1$ ～ $1$ とすると、$\log(1+t)$ に $t=-1$ を代入しなければならなくなるので、対称性から $0$ ～ $1$ として $t=-1$ の代入を避けましょう。

まとめ

今回は、京都大学理系数学（2020年 第6問）の解説をしました。